计算机图形学入门笔记（四）（L13-L16）

L13 Ray Tracing1（Whitted-Style Ray Tracing）

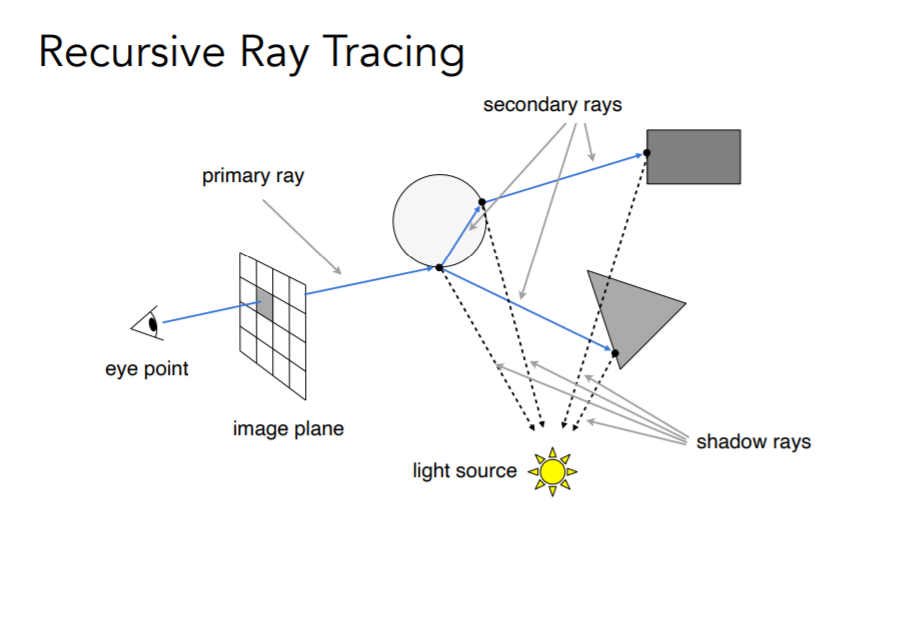
avater
基本操作如上
就是对于每个像素点，将这个点与相机连线，这一束光打在其他物体上，最后能到达光源的能量总和作为该点亮度
对于一根从光源射出的射线，记$\pmb{r}(t)=\pmb{o}+t\pmb{d}$，其中$\pmb{o}$为原点（也就是光源坐标），$\pmb{d}$为方向，$t\geq 0$

直线与球的交点

\[Sphere:(\pmb{p}-\pmb{c})^2=R^2 \]

其中$\pmb{p},\pmb{c}$为点的坐标和圆心坐标
联立得

\[(\pmb{o}+t\pmb{d}-\pmb{c})^2-R^2=0\\ t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}~where\\ a=\pmb{d}*\pmb{d}\\ b=2(\pmb{o}-\pmb{c})*d\\ c=(\pmb{o}-\pmb{c})*(\pmb{o}-\pmb{c})-R^2\]

一般的显式方程$f(p)=0$
带入得$f(\pmb{o}+t\pmb{d})=0$
我们只要求正的实根
与三角形面片
我们只要先与这个三角形所在的平面算交点，再判断这个交点是不是在三角形内即可
平面方程$(\pmb{p}-\pmb{p_0})*\pmb{n}=0$
带入解得

\[t=\frac{(\pmb{p_0}-\pmb{o})*\pmb{n}}{\pmb{d}*\pmb{n}} \]

判断点是否在三角形内之前讲过，直接三个叉乘
Moller Trumbore Algorithm
通过重心坐标直接判断
具体操作是解线性方程组
推导：

扫描二维码关注公众号，回复： 11440138 查看本文章

\[\begin{aligned} (1-b_1-b_2)\pmb{p_0}+b_1\pmb{p_1}+b_2\pmb{p_2}&=\pmb{o}+t\pmb{d} \\ -t*\pmb{d}+b_1(\pmb{p_1}-\pmb{p_0})+b_2(\pmb{p_2}-\pmb{p_0})&=\pmb{o}-\pmb{p_0} \end{aligned} \]

令$\vec{e_1} = p_1 - p_0, \vec{e_2} = p_2 - p_0, \vec{s} = o-p_0$
即$$-t*\pmb{d}+b_1\pmb{e_1}+b_2\pmb{e_2}=\pmb{s}$$
由于这些向量有三个坐标，方程有三个未知数，因而可以解出

\[\begin{bmatrix} t \\ b_1 \\ b_2 \end{bmatrix} = \frac{1} {(-\vec{d}\times \vec{e_2}) \cdot \vec{e_1} }* \begin{bmatrix} (\vec{s}\times \vec{e_2}) \cdot \vec{e_1}\\ (-\vec{d}\times \vec{e_2}) \cdot \vec{s}\\ (-\vec{d}\times \vec{s}) \cdot \vec{e_1} \end{bmatrix}\]

也等于

\[\begin{bmatrix} t \\ b_1 \\ b_2 \end{bmatrix} = \frac{1} {(\vec{d}\times \vec{e_2}) \cdot \vec{e_1} }* \begin{bmatrix} (\vec{s}\times \vec{e_1}) \cdot \vec{e_2}\\ (\vec{d}\times \vec{e_2}) \cdot \vec{s}\\ (\vec{s}\times \vec{e_1}) \cdot \vec{d} \end{bmatrix}\]

令$\vec{s_1}=\vec{d}\times\vec{e_2},\vec{s_2}=\vec{s}\times\vec{e_1}$

\[\begin{bmatrix} t \\ b_1 \\ b_2 \end{bmatrix} = \frac{1} {\vec{s_1} \cdot \vec{e_1} }* \begin{bmatrix} \vec{s_2} \cdot \vec{e_2}\\ \vec{s_1} \cdot \vec{s}\\ \vec{s_2} \cdot \vec{d} \end{bmatrix}\]

若线与平面相交，则$t\geq 0$
若线与三角形相交，则$t\geq 0$且$0\leq b_1,b_2$且$b_1+b_2\leq 1$

Axis-Aligned Bounding Box（轴对称包围盒）
对一个物体求一个包围盒，也就是在三个维度上的左边界，右边界所围成的区域
因而可以算出来对于每一根轴（比如说x轴的）$t_{x~enter},t_{x~exit}$
所以光线在这个包围盒内部的部分就是$t_{x~enter}\leq t\leq t_{x~exit}$
对三根轴分别考虑，$t_{enter}=\max{t_{enter}},t_{exit}=\min{t_{exit}}$
所以如果$t_{enter}<t_{exit}$则这束光与Bounding Box有交点
有两种特殊情况：

$t_{exit}<0$，此时包围盒必定在原点的反方向，所以没有交点
$t_{exit}\geq 0$且$t_{enter}<0$，此时原点必定在包围盒内，所以必有交点
所以综上，光线和包围盒有交点当且仅当$t_{enter}<t_{exit}$且$t_{exit}\geq 0$

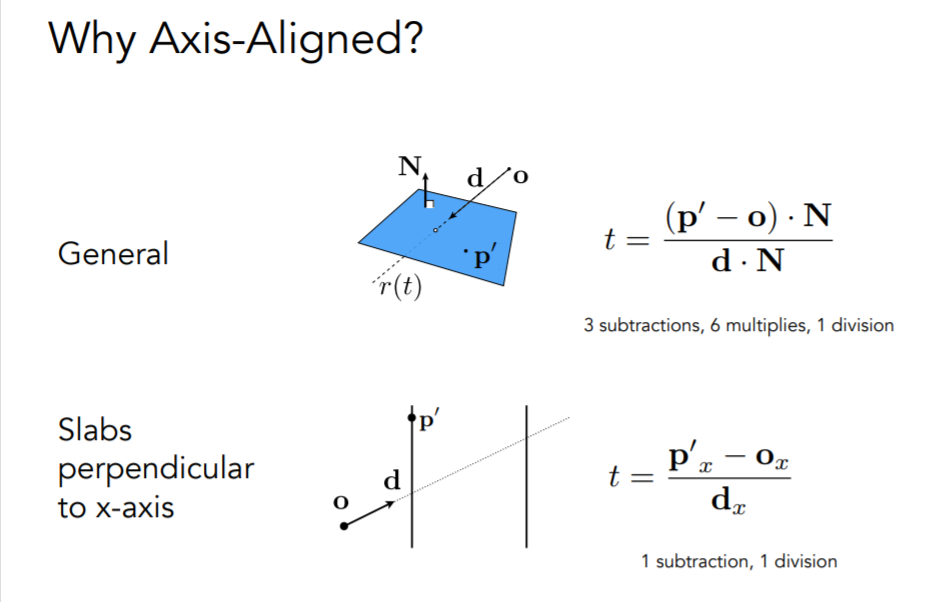
为什么用这个？直接看图吧
avater

L14 Ray Tracing 2 (Acceleration&Radiometry)

加速结构：
Spatial Partition（空间划分）

Uniform（Grids）

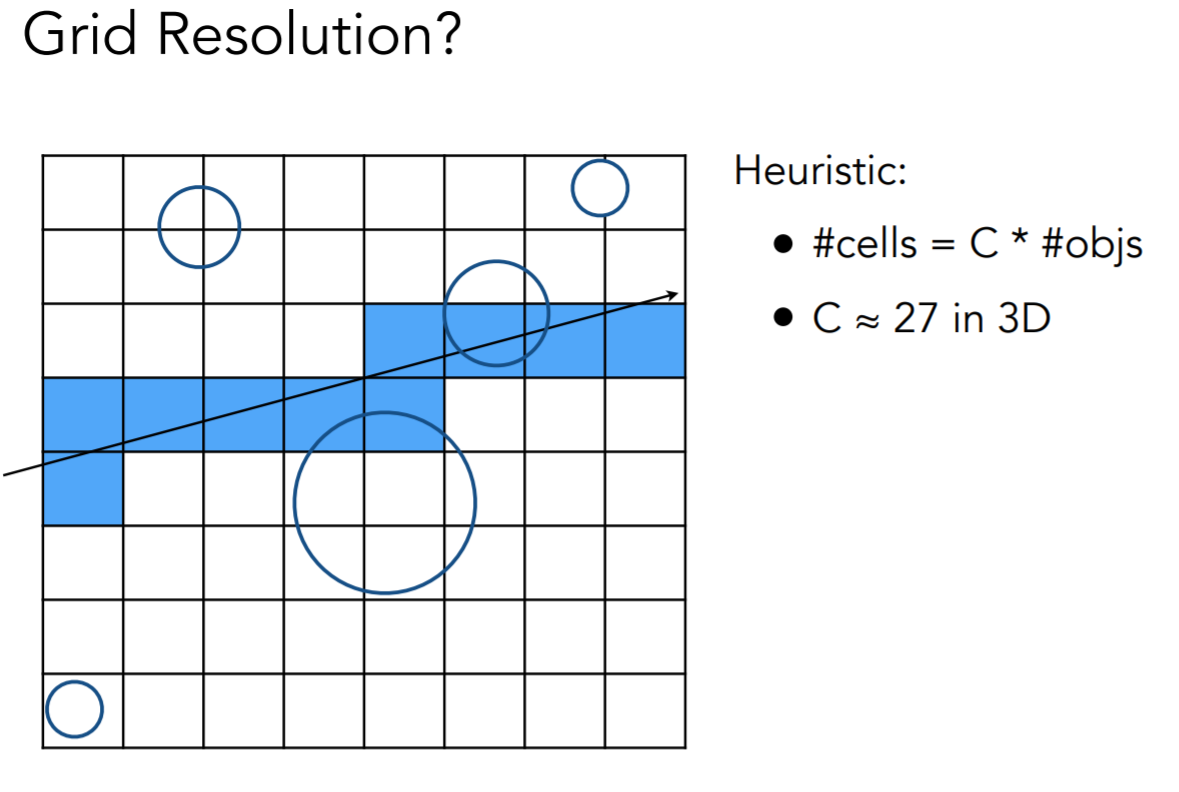
标记每一个存在物体表面（比如上图的圆环）的格子
如果光线通过被标记的格子，再去看和物体是否相交
在物体多且均匀的时候比较好用
四/八/$(2^n)$叉树
BSP-Tree 二叉树
KD-Tree
建树：
非叶结点存储：
在哪个轴划分，划分的坐标
指向子结点的指针
叶节点存储：
物体列表
工作：
如果光线和这个结点代表的Box有交点，递归到子节点
如果这个结点是叶结点，判定与Box内物体是否有交点
缺点：
三角形和Box求交并不好求，且一个物体会被存储在多个叶结点内

Object Partition（物体划分）
Bounding Volume Hierarchy(BVH)
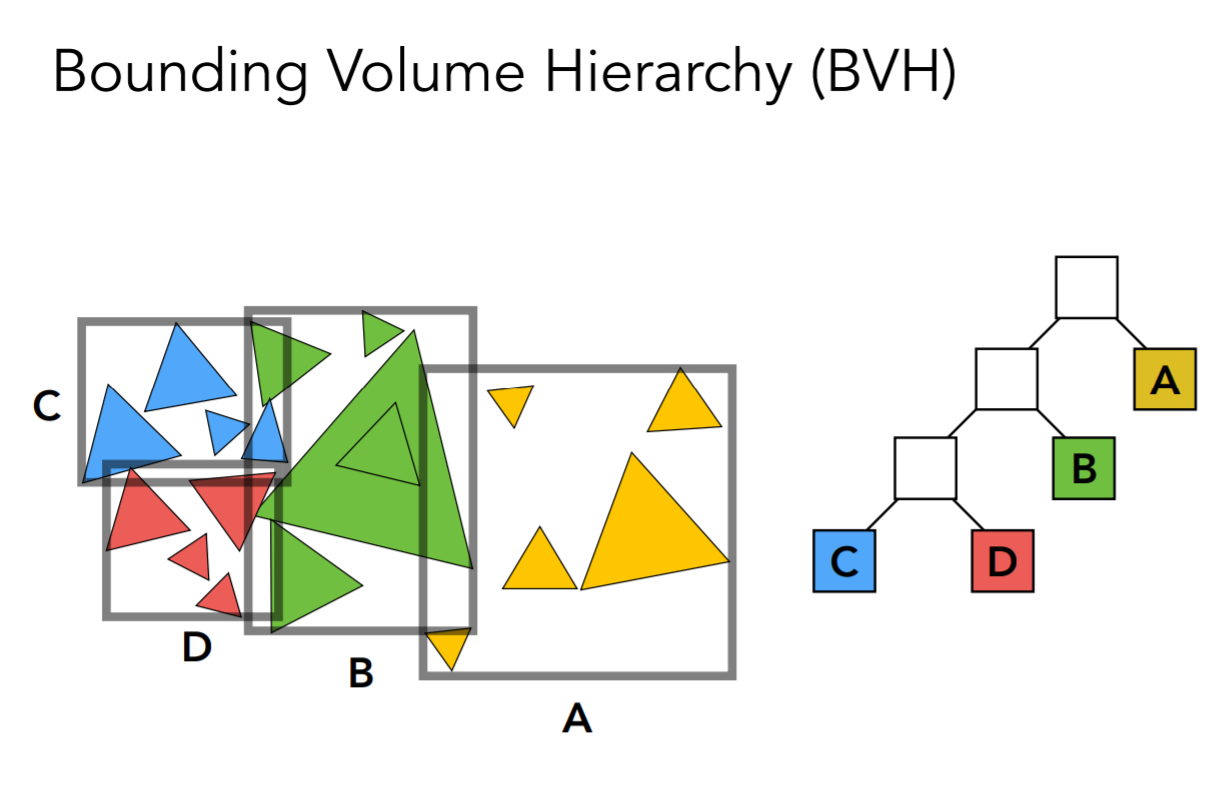
avater
划分方法：

选最长的轴划分
在中间的三角形处划分
非叶节点存储：
Box，指向子结点的指针
叶结点存储：
Box，物体列表

优：每个物体只会在一个Box里（实现容易）
缺：各个Box可能重叠

L15 Ray Tracing 3 (Light Transport&Global Illumination)

Radiometry（辐射度量学）

Definition:Radiant energy is the energy of electromagneticradiation.
It is measured in units of joules, and denoted by the symbol $Q[J]$

Definition:Radiant flux (power) is the energy emitted, reflected, transmitted or received, per unit time.

\[\Phi=\frac{dQ}{dt}[W/lu(lumen)] \]

Definition:The radiant (luminous) intensity is the power per unit solid angle emitted by a point light source.

\[I(\omega)=\frac{d\Phi}{d\omega}[\frac{W}{sr}=\frac{lm}{sr}=cd(candela)] \]

Defination:Solid angle is the ratio of subtended area on sphere to radius squared.**

\[\Omega=\frac{A}{r^2} where~A~is~an~Area\\ dA=r^2sin\theta d\theta d\phi\\ d\omega=\frac{dA}{r^2}=sin\theta d\theta d\phi\]

Isotropic Point Source（各向同性点光源）

\[\Phi=\int_{S^2}Id\omega=4\pi I\\ I=\frac{\Phi}{4\pi}\]

Definition: The irradiance is the power per unit area(projected) incidention a surface point.

\[E(\pmb{x})=\frac{d\Phi({\pmb{x}})}{dA}[\frac{W}{m^2}=\frac{lm}{m^2}=lux] \]

Definition: The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.

\[L(p,\omega)=\frac{d^2\Phi(p,\omega)}{d\omega dA} \]

• Radiance: Irradiance per solid angle
• Radiance: Intensity per projected unit area

Bidirectional Reflectance Distribution Function (BRDF)
双向反射分布函数：从某个方向射入的光线，在经过表面反射后在各个方向上的能量分布情况

反射方程
对入射光线分析

\[dE(\omega_i)=L(\omega_i)d\omega_i \]

对出射光线分析

\[dL(\omega_r) \]

所以有BRDF函数

\[f(\omega_i\to \omega_r)=\frac{dL(\omega_r)}{dE(\omega_i)}[\frac{1}{sr}] \]

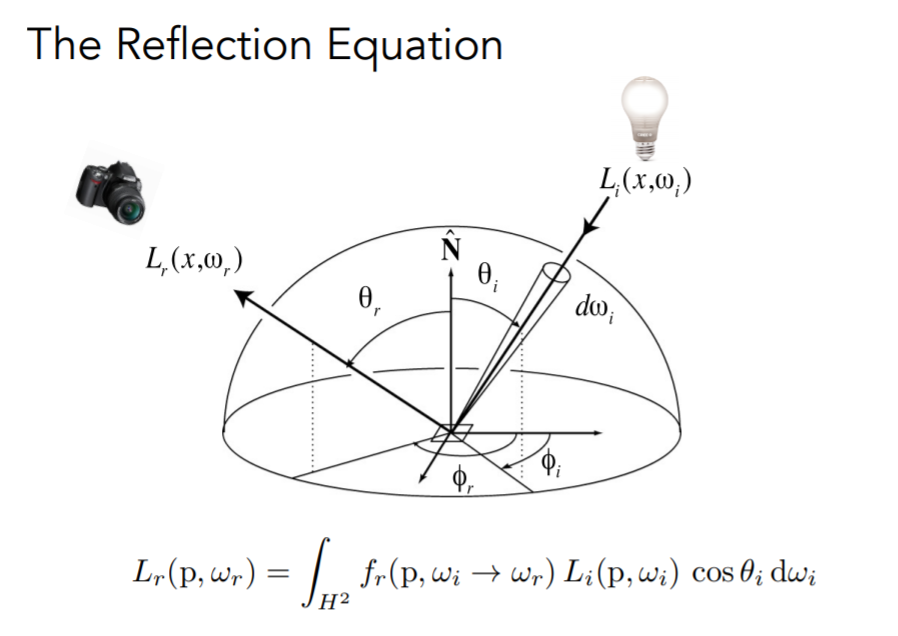
avater
解释：对于一个方向$r$所收到的光线，等于把所有方向入射然后再反射到这个方向的能量积分
$p$是面积，$H^2$是Unit Hemisphere（单位半球），$cos\theta_i$这一项是因为前面那些面积都是投影面积，所以要乘一个$cos\theta_i$（类比一下向量点乘，和之前的blinn-phong光照模型）
然而众所周知，光线可以~~射来射去~~，也就是说这个地方的出射光线可能又会影响到入射光线
~~套娃警告~~

渲染方程
考虑到物体本身也可能会发光

\[L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}{L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n*\omega_i)d\omega_i} \]

其中$L_e$这一项是自身发光，$\Omega^+$是指能射到该点的区域，之前直接取了上半球面，$n*\omega_i$相当于$cos\theta_i$（因为两个都是单位向量）
注意：和blinn-phong模型一样，这里假定所有方向都是从这个点指向外面的！

渲染方程的求解方法
~~没听懂，果然还要去学数值计算啊~~

\[\color{red}{L_r(x,\omega_r)}=L_e(x,\omega_r)+\int_{\Omega}{\color{red}{L_r(x,\omega_i)}f(x,\omega_i,\omega_r)(n*\omega_i)d\omega_i} \]

上面标红的是未知项，其它的都是已知项
所以我们可以简写为一个算子方程

\[\color{red}{L(u)}=e(u)+\int{\color{red}{L(v)}K(u,v)dv} \]

最后那个$K$被称为核函数，或者是光线传播算子
然后我们可以把它变成一个乘积形式（可能是卷积？？？）
然后变成了一个矩阵方程

\[\begin{aligned} \color{red}{L}&=E+K\color{red}{L} \\ (I-K)\color{red}{L}&=E \\ \color{red}{L}&=(I-K)^{-1}E \\ &=(I+K+K^2+K^3+...)E \\ &=E+KE+K^2E+K^3E+... \end{aligned} \]

~~这个展开，很nb~~
所以我们可以直接取前几项算，其中$E$是物体本身光线，$KE$是被照射的光线，$K$的多少次方就是经过多少次反射（散射，折射等等）后再打到物体表面
其中二次以上的统称为全局光照，光栅化一般只能处理局部光照（也就是零次和一次项）

L16 Ray Tracing 4 (Monte Carlo Path Tracing)

前置：蒙特卡罗积分（数值积分）
就是直接采样，取点平均

\[\int f(x)dx=\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)} \]

Path Tracing
引入：前面学的 Whitted-Style Ray Tracing 的问题：

镜面就全部镜面反射
漫反射处不继续反射，直接计算阴影

计算的话之前套蒙特卡罗和上面那个渲染方程，其中$p=\frac{1}{2\pi}$（因为是对半球面积分，而整个球面的立体角是$4\pi$）

所以我们可以写出伪代码

shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
    Return Lo

其中$L_i$是光源强度，$pdf$是概率密度函数，就是$p$

然而有一个问题：如果一束光先打到某一个物体，再打到这个物体上，这一部分并没有被计算
所以更新版本

shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

还有一个问题：每个点都去取，比如说$100$束光，那么这样下去要$trace$的光数量会指数上涨（每次乘100）
所以我们每次只取一束光

shade(p, wo)
    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi)
    Else If ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi)

Path Tracing指的就是这种只取一束的
但是这样误差有点大
但是我们是对每一个像素计算
所以相机对像素内随机许多点发出一束光即可

ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p
            pixel_radiance += 1 / N * shade(p, sample_to_cam)
    Return pixel_radiance

然而还有一个问题：递归的终止条件是什么？
俄罗斯轮盘赌（RR）！
~~奇怪的命名增加了~~
首先设置一个概率$P$
对于每一次调用$shade$函数，

以概率$P$接受，最后返回$\frac{L_o}{P}$
以概率$1-P$拒绝，直接返回0
这个方法的妙处在于$E(L_0)=P*\frac{L_0}{P}+(1-P)*0=L_o$
也就是期望不变！

Manually specify a probability P_RR

shade(p, wo)
    Randomly select ksi in a uniform dist. in [0, 1]
    If (ksi > P_RR) return 0.0;
    
    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR

问题是无穷无尽的：
如果光源占的立体角很小，那么就会有很多光线被浪费掉，性能损耗大
所以我们可以通过换元，换成对面积积分

\[d\omega=\frac{dA\cos \theta'}{|x'-x|^2} \]

渲染方程重写一遍：
avater

进一步优化：
光源来的光线可以无视多次弹射，直接计算（通过换元对面积积分），所以也不需要RR
其他物体弹射的光线需要RR，不需要换元

shade(p, wo)
    # Contribution from the light source.
    Uniformly sample the light at x’ (pdf_light = 1 / A)
    If the ray is not blocked
        L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light
    
    # Contribution from other reflectors.
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
        If ray r hit a non-emitting object at q
            L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR
    Return L_dir + L_indir