Locality Sensitive Hashing for Similar Item Search
An efficient approach to identifying approximate nearest neighbors.

Motivation
Everyone is aware of Shazam, the app that let’s you identify any song within seconds. The speed at which it identifies songs not only amazed me but also made me wonder how they are able to do this with a massive database of songs (~10 million). I realized this can be done using audio fingerprinting and Locality Sensitive Hashing (I’m pretty sure Shazam uses some advanced techniques). This article is an attempt to explain the steps and concepts involved in implementing a program to perform music search (similar item search in general).
Audio fingerprinting is the process of identifying unique characteristics from a fixed duration audio stream. Such unique characteristics can be identified for all existing songs and stored in a database. When we hear a new song, we can extract similar characteristics from the recorded audio and compare against the database to identify the song. However, in practice there will be two challenges with this approach:
- High dimensionality of the unique characteristic/feature vector required to identify songs
- Comparison of the recorded audio features against features of all songs in the database is expensive in terms of time and memory
The first challenge can be addressed using a dimensionality reduction technique like PCA and the second using a combination of clustering and nearest neighbor search. Locality Sensitive Hashing (hereon referred to as LSH) can address both the challenges by
- reducing the high dimensional features to smaller dimensions while preserving the differentiability
- grouping similar objects (songs in this case) into same buckets with high probability
Applications of LSH
Before jumping into understanding LSH, it is worth noting that the application areas include
- Recommender systems
- Near-duplicate detection (document, online news articles, etc.)
- Hierarchical clustering
- Genome-wide association study
- Image similarity identification (VisualRank)
- Audio similarity identification
- Digital video fingerprinting
Uber used LSH to detect platform abuses (fake accounts, payment fraud, etc.). A Shazam styled app or Youtube sized recommender system can be built using LSH.
What is LSH?
LSH is a hashing based algorithm to identify approximate nearest neighbors. In the normal nearest neighbor problem, there are a bunch of points (let’s refer to these as training set) in space and given a new point, objective is to identify the point in training set closest to the given point. Complexity of such process is linear [for those familiar with Big-O notation, O(N), where N is the size of training set]. An approximate nearest neighboring algorithm tries to reduce this complexity to sub-linear (less than linear but can be anything). Sub-linear complexity is achieved by reducing the number of comparisons needed to find similar items.
LSH works on the principle that if there are two points in feature space closer to each other, they are very likely to have same hash (reduced representation of data). LSH primarily differs from conventional hashing (aka cryptographic) in the sense that cryptographic hashing tries to avoid collisions but LSH aims to maximize collisions for similar points. In cryptographic hashing a minor perturbation to the input can alter the hash significantly but in LSH, slight distortions would be ignored so that the main content can be identified easily. The hash collisions make it possible for similar items to have a high probability of having the same hash value.
///LSH的工作原理是,如果要素空间中有两个点彼此靠近,则它们很可能具有相同的哈希值(数据的简化表示)。 LSH与常规哈希(aka加密)的主要区别在于,加密哈希试图避免冲突,但LSH的目的是使相似点的冲突最大化。 在加密哈希中,对输入的微小扰动会显着改变哈希,但在LSH中,轻微的失真将被忽略,以便可以轻松识别主要内容。 哈希冲突使相似项具有相同哈希值的可能性很高。///
Locality Sensitive Hashing (LSH) is a generic hashing technique that aims, as the name suggests, to preserve the local relations of the data while significantly reducing the dimensionality of the dataset.
Now that we have established LSH is a hashing function that aims to maximize collisions for similar items, let’s formalize the definition:
A hash function h is Locality Sensitive if for given two points a, b in a high dimensional feature space, 1. Pr(h(a) == h(b)) is high if a and b are near 2. Pr(h(a) == h(b)) is low if a and b are far 3. Time complexity to identify close objects is sub-linear.
Implementation of LSH
Having learnt what LSH is, it’s time to understand how to implement it. Implementing LSH is down to understanding how to generate hash values. Some popular approaches to construct LSH are
- Min-wise independent permutations
- Nilsimsa Hash (Anti-Spam focused)
- TLSH (For security and digital forensic applications)
- Random Projection aka SimHash
In this article, I’ll give a walkthrough of implementing LSH using random projection method. Curious readers can learn about the other methods from the linked urls.
Detour — Random Projection Method
Random projection is a technique for representing high-dimensional data in low-dimensional feature space (dimensionality reduction). It gained traction for its ability to approximately preserve relations (pairwise distance or cosine similarity) in low-dimensional space while being computationally less expensive.
The core idea behind random projection is that if points in a vector space are of sufficiently high dimension, then they may be projected into a suitable lower-dimensional space in a way which approximately preserves the distances between the points.
Above statement is an interpretation of the Johnson-Lindenstrauss lemma.
Consider a high-dimensional data represented as a matrix D, with n observations (columns of matrix) and d features (rows of the matrix). It can be projected onto a lower dimensional space with k-dimensions, where k<<d, using a random projection matrix R. Mathematically, the lower dimensional representation P can be obtained as
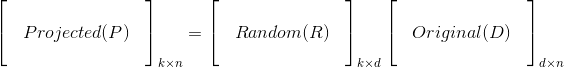
Columns of the random projection matrix R are called random vectors and the elements of these random vectors are drawn independently from gaussian distribution (zero mean, unit variance).
LSH using Random Projection Method
In this LSH implementation, we construct a table of all possible bins where each bin is made up of similar items. Each bin will be represented by a bitwise hash value, which is a number made up of a sequence of 1’s and 0’s (Ex: 110110, 111001). In this representation, two observations with same bitwise hash values are more likely to be similar than those with different hashes. Basic algorithm to generate a bitwise hash table is
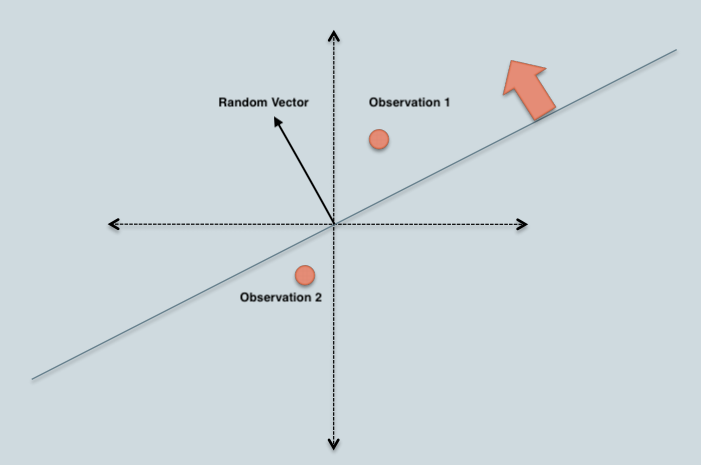
Dot product of random vector and observation 1 > 0, which gives a bit value of 1. Similarly, dot product of random vector and observation 2 < 0 and the resulting bit value will be 0.
- Create
krandom vectors of lengthdeach, wherekis the size of bitwise hash value anddis the dimension of the feature vector. - For each random vector, compute the dot product of the random vector and the observation. If the result of the dot product is positive, assign the bit value as 1 else 0
- Concatenate all the bit values computed for
kdot products - Repeat the above two steps for all observations to compute hash values for all observations
- Group observations with same hash values together to create a LSH table
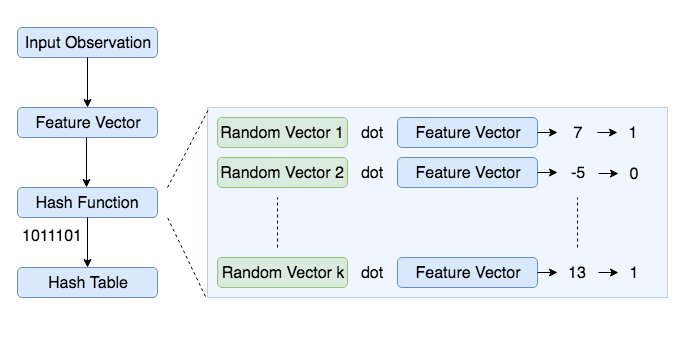
Below is a code snippet to construct such hash table:
| import numpy as np | |
|---|---|
| class HashTable: | |
| def init(self, hash_size, inp_dimensions): | |
| self.hash_size = hash_size | |
| self.inp_dimensions = inp_dimensions | |
| self.hash_table = dict() | |
| self.projections = np.random.randn(self.hash_size, inp_dimensions) | |
| def generate_hash(self, inp_vector): | |
| bools = (np.dot(inp_vector, self.projections.T) > 0).astype('int') | |
| return ''.join(bools.astype('str')) | |
| def setitem(self, inp_vec, label): | |
| hash_value = self.generate_hash(inp_vec) | |
| self.hash_table[hash_value] = self.hash_table\ | |
| .get(hash_value, list()) + [label] | |
| def getitem(self, inp_vec): | |
| hash_value = self.generate_hash(inp_vec) | |
| return self.hash_table.get(hash_value, []) | |
| hash_table = HashTable(hash_size=4, inp_dimensions=20) |
转自:
https://towardsdatascience.com/locality-sensitive-hashing-for-music-search-f2f1940ace23