VIN3.系统初始化

引言
1.初始化流程
2.CalibrationExRotation
3.检测 IMU 可观性
4.relativePose
5.GlobalSFM.construct
6.visualInitialAlign

6.1.陀螺仪 bias 校正
6.2.初始化速度、重力和尺度因子
6.3.修正重力矢量

引言

搬运工 + 自己阅读代码理解。

参考说明

pipeline如图：
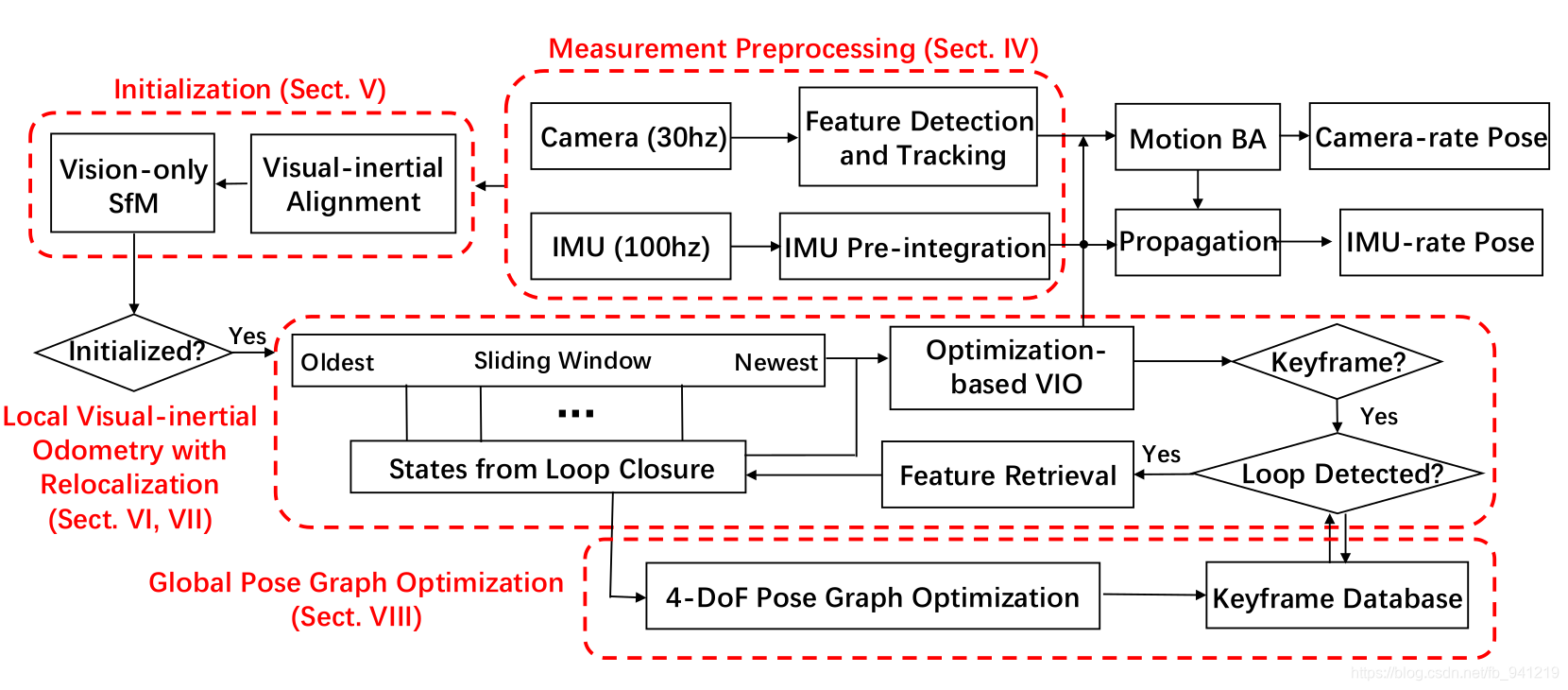
在这里插入图片描述
本节则是阅读总结Initialization部分。estimator.cpp-->processImage().

在提取的图像的 Features 和做完 IMU 的预积分之后,进入了系统的初始化环节,首先,利用 SFM 进行纯视觉估计滑窗内所有帧的位姿及 3D 点逆深度,最后与 IMU 预积分进行对齐求解初始化参数。主要的目的有以下两个:

系统使用单目相机,如果没有一个良好的尺度估计,就无法对两个传感器做进一步的融合,这个时候需要恢复出尺度;
要对 IMU 进行初始化,IMU 会受到 bias 的影响,所以要得到 IMU 的 bias。

所以需要从初始化中恢复出尺度、重力、速度以及 IMU 的 bias,因为视觉 (SFM) 在初始化的过程中有着较好的表现,所以在初始化的过程中主要以 SFM 为主,然后将 IMU 的预积分结果与其对齐，即可得到较好的初始化结果。初始化采用视觉和 IMU 的松耦合方案,首先用 SFM 求解滑窗内所有帧的位姿,和所有路标点的 3D 位置,然后跟 IMU 预积分的值对齐,求解重力方向、尺度因子、陀螺仪 bias 及每一帧对应的速度。

1.初始化流程

初始化的流程图如下所示:

首先,对代码中几个易混变量进行说明:

传到 processImage 的 image 表示当前帧跟踪到上一帧中的特征点集合,也就是当前帧观测到的所有的路标点(不包括在当前帧新提取的点),如VIN1.视觉前端表中 track_cnt≥2 的 feature,image 类型为:

FeatureManager 中几个变量:

VINS里面分四步进行estimator.cpp-->processImage():

1.第一个就是旋转外参校准;
2.第二个就是找到某帧作为系统初始化原点，计算3D地图点;(下面的相机初始化)
3.第三就是将相机坐标系转到IMU坐标系中;
4.第四就是相机与IMU对齐，包括IMU零偏初始化，速度，重力向量，尺度初始化.

相机初始化estimator.cpp-->processImage()-->initialStructure()函数：

先判断IMU是否有足够的variance, 求all_image_frame中所有帧的平均加速度, 并计算加速度的方差, 判断方差是否足够大

调用relativePose判断sliding window是否某一帧l与当前帧视差足够大, 如果存在的话, 则根据特征匹配用五点法计算l和当前帧的relative R,t, 用来做后面的SFM

调用GlobalSFM.construct进行SFM, 估计slidingwindow中的camera pose和features的3D position.

然后对all_image_frame中没有参与SFM的帧的位姿进行了PnP求解.

调用visualInitialAlign()进行视觉和IMU的校准.

简洁：

求取本质矩阵求解位姿(relativePose)

三角化特征点(sfm.construct)

PnP 求解位姿(cv::solvePnP)

转换到 IMU 坐标系下

$c_0$ 坐标系作为参考系

不断重复直到恢复出滑窗内的 Features 和相机位姿

2.CalibrationExRotation

estimator.cpp-->processImage()-->CalibrationExRotation()；转换为数学模型实际就是求解超定方程组，可以利用最小二乘也可以使用奇异值分解，由于一般不满秩故采用奇异值分解求解。
　　相对旋转是相机与 IMU 之间外参的一部分。相机与 IMU 之间的旋转标定非常重要,偏差 $1～2^{\circ}$ ，系统的精度就会变得很低。通过视觉 SFM 获取了相邻两关键帧之间相机的相对旋转 $R_{c_{k+1}}^{c_{k}}$ ,IMU 经过预积分得到的旋转矩阵为 $R_{b_{k+1}}^{b_{k}}$ 。相机与 IMU 之间的相对旋转为 $R_{c}^{b}$ ,则对于任一帧满足：
$R_{b_{k+1}}^{b_{k}} R_{c}^{b}=R_{c}^{b} R_{c_{k+1}}^{c_{k}}\tag{1}$ 将旋转矩阵写为四元数,则上式可以写为 $q_{b_{k+1}}^{b_{k}} \otimes q_{c}^{b}=q_{c}^{b} \otimes q_{c_{k+1}}^{c_{k}}\tag{2}$ 将其写为左乘和右乘的形式 $\left(\left[q_{b_{k+1}}^{b_{k}}\right]_{L}-\left[q_{c_{k+1}}^{c_{k}}\right]_{R}\right) q_{c}^{b}=Q_{k+1}^{k} q_{c}^{b}=0\tag{3}$ $[q]_{L}$ 、 $[q]_{R}$ 分别表示四元数左乘矩阵和四元数右乘矩阵,其定义为(四元数实部在后) $L=\left[\begin{array}{cc}{q_{w} I_{3}+\left[q_{x y z}\right]_{ \times}} & {q_{x y z}} \\ {-q_{x y z}} & {q_{w}}\end{array}\right]$ $[q]_{R}=\left[\begin{array}{cc}{q_{w} I_{3}-\left[q_{x y z}\right]_{ \times}} & {q_{x y z}} \\ {-q_{x y z}} & {q_{w}}\end{array}\right]\tag{4}$ 那么对于 n 对测量值,则有 $\left[\begin{array}{c}{w_{1}^{0} Q_{1}^{0}} \\ {w_{2}^{1} Q_{2}^{1}} \\ {\vdots} \\ {w_{N}^{N-1} Q_{N}^{N-1}}\end{array}\right] q_{c}^{b}=Q_{N} q_{c}^{b}=0\tag{5}$ 其中 $w_{N}^{N-1}$ 为外点剔除权重,其与相对旋转求得的角度残差有关, $N$ 为计算相对旋转需要的测量对数,其由最终的终止条件决定。角度残差可以写为 $\theta_{k+1}^{k}=\arccos \left(\frac{\operatorname{tr}\left(\hat{R}_{c}^{b^{-1}} R_{b_{k+1}}^{b_{k}^{-1}} \hat{R}_{c}^{b} R_{c_{k+1}}^{c_{k}}\right)-1}{2}\right)\tag{6}$
从而权重为 $w_{k+1}^{k}=\left\{\begin{array}{cc}{1,} & {\theta_{k+1}^{k}<\text {threshold}（一般为5~度） } \\ {\frac{t h r e s h o l d}{\theta_{k+1}^{k}},} & {\text {otherwise}}\end{array}\right.\tag{7}$ 至此,就可以通过求解方程 $Q_{N} q_{c}^{b}=0$ 得到相对旋转，解为 $Q_{N}$ 的左奇异向量中最小的奇异值对应的特征向量(是最小二乘法的最优解，之前证明过)
　　但是,在这里还要注意求解的终止条件 (校准完成的终止条件) 。在足够多的旋转运动中,我们可以很好的估计出相对旋转 $R_{c}^{b}$ ,这时 $Q_{N}$ 对应一个准确解,且其零空间的秩为 1。但是在校准的过程中,某些轴向上可能存在退化运动 (如匀速运动),这时 $Q_{N}$ 的零空间的秩会大于 1。判断条件就是 $Q_{N}$ 的第二小的奇异值是否大于某个阈值，若大于则其零空间的秩为1，反之秩大于1，相对旋转 $R_{c}^{b}$ 的精度不够，校准不成功。

bool InitialEXRotation::CalibrationExRotation(vector<pair<Vector3d, Vector3d>> corres, Quaterniond delta_q_imu, Matrix3d &calib_ric_result)
{
    //! Step1：滑窗内的帧数加1
    frame_count++;

    //! Step2:计算两帧之间的旋转矩阵
    Rc.push_back(solveRelativeR(corres));

    //! IMU 预积分得到的旋转
    Rimu.push_back(delta_q_imu.toRotationMatrix());
    Rc_g.push_back(ric.inverse() * delta_q_imu * ric);

    Eigen::MatrixXd A(frame_count * 4, 4);
    A.setZero();
    int sum_ok = 0;
    for (int i = 1; i <= frame_count; i++)
    {
        Quaterniond r1(Rc[i]);
        Quaterniond r2(Rc_g[i]);

        //！Step3:求取估计出的相机与IMU之间旋转的残差
        double angular_distance = 180 / M_PI * r1.angularDistance(r2);
        //ROS_DEBUG("%d %f", i, angular_distance);

        //! Step4:计算外点剔除的权重
        double huber = angular_distance > 5.0 ? 5.0 / angular_distance : 1.0;
        ++sum_ok;
        Matrix4d L, R;

        //! Step5：求取系数矩阵，公式(3)的系数矩阵Q
        //! 得到相机对极关系得到的旋转q的左乘
        double w = Quaterniond(Rc[i]).w();
        Vector3d q = Quaterniond(Rc[i]).vec();
        L.block<3, 3>(0, 0) = w * Matrix3d::Identity() + Utility::skewSymmetric(q);
        L.block<3, 1>(0, 3) = q;
        L.block<1, 3>(3, 0) = -q.transpose();
        L(3, 3) = w;

        //! 得到由IMU预积分得到的旋转q的右乘
        Quaterniond R_ij(Rimu[i]);
        w = R_ij.w();
        q = R_ij.vec();
        R.block<3, 3>(0, 0) = w * Matrix3d::Identity() - Utility::skewSymmetric(q);
        R.block<3, 1>(0, 3) = q;
        R.block<1, 3>(3, 0) = -q.transpose();
        R(3, 3) = w;
		//拼接大矩阵Q，公式(5)的系数矩阵Q
        A.block<4, 4>((i - 1) * 4, 0) = huber * (L - R);
    }

    //！Step6：通过SVD分解，求取相机与IMU的相对旋转
    //！解为系数矩阵A的右奇异向量V中最小奇异值对应的特征向量
    JacobiSVD<MatrixXd> svd(A, ComputeFullU | ComputeFullV);
    Matrix<double, 4, 1> x = svd.matrixV().col(3);
    Quaterniond estimated_R(x);
    ric = estimated_R.toRotationMatrix().inverse();
    //cout << svd.singularValues().transpose() << endl;
    //cout << ric << endl;

    //！Step7：判断对于相机与IMU的相对旋转是否满足终止条件
    //！1.用来求解相对旋转的IMU-Cmaera的测量对数是否大于滑窗大小。
    //！2.A矩阵第二小的奇异值是否大于某个阈值，使A得零空间的秩为1
    Vector3d ric_cov;
    ric_cov = svd.singularValues().tail<3>();
    if (frame_count >= WINDOW_SIZE && ric_cov(1) > 0.25)
    {
        calib_ric_result = ric;
        return true;
    }
    else
        return false;
}

接下来介绍estimator.cpp-->processImage()-->initialStructure()函数流程：

在这里插入图片描述

3.检测 IMU 可观性

estimator.cpp-->processImage()-->initialStructure()：通过计算线加速度的标准差，判断IMU是否有充分运动激励，以进行初始化注意这里并没有算上all_image_frame的第一帧，所以求均值和标准差的时候要减一。参考文章为什么标准差可以代表可观性？

// 计 算 均 值
map<double, ImageFrame>::iterator frame_it;
Vector3d sum_g;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
    double dt = frame_it->second.pre_integration->sum_dt;
    Vector3d tmp_g = frame_it->second.pre_integration->delta_v / dt;
    sum_g += tmp_g;
}
// 计 算 方 差
Vector3d aver_g;
aver_g = sum_g * 1.0 / ((int)all_image_frame.size() - 1);
double var = 0;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
    double dt = frame_it->second.pre_integration->sum_dt;
    Vector3d tmp_g = frame_it->second.pre_integration->delta_v / dt;
    var += (tmp_g - aver_g).transpose() * (tmp_g - aver_g);
    //cout << "frame g " << tmp_g.transpose() << endl;
}
// 计 算 标 准 差
var = sqrt(var / ((int)all_image_frame.size() - 1));
//ROS_WARN("IMU variation %f!", var);
if (var < 0.25)// ! 以 标 准 差 判 断 可 观 性
{
    // ROS_INFO("IMU excitation not enouth!");
    //return false;
}

4.relativePose

estimator.cpp-->processImage()-->initialStructure()-->relativePose();在滑窗内寻找与当前帧的匹配特征点数较多的关键帧作为参考帧, 并通过求本质矩阵（E）cv::findFundamentalMat 计算出当前帧到参考帧的 T;参考E2Rt.

/**
 * [Estimator::relativePose 在滑窗中寻找与最新的关键帧共视关系较强的关键帧]
 * @param  relative_R [description]
 * @param  relative_T [description]  window_size ==> i
 * @param  l          [description]
 * @return            [description]
 */
bool Estimator::relativePose(Matrix3d &relative_R, Vector3d &relative_T, int &l)

solve_Spts.cpp–>solveRelativeRT()

/**
 * [MotionEstimator::solveRelativeRT 利用5点法求解变换矩阵T]
 * @param  corres      [匹配点]
 * @param  Rotation    [旋转量]
 * @param  Translation [平移量]
 * @return             [description]
 */
 bool MotionEstimator::solveRelativeRT(const vector<pair<Vector3d, Vector3d>> &corres, Matrix3d &Rotation, Vector3d &Translation)

这个函数调用opencv函数：cv::Mat E = cv::findFundamentalMat(*)求解出本质矩阵E,再利用E求解出T(R、t)参考E2Rt.VINs中代码solve_Spts.cpp-->recoverPose如下：

    /**
     * 从本质矩阵中恢复出变换矩阵
     * 函数调用decomposeEssentialMat()利用SVD分解求解出四中可能然后再验证出符合要求的唯一解，和十四讲中的计算是一样的！
     * @param E
     * @param _points1
     * @param _points2
     * @param _cameraMatrix
     * @param _R
     * @param _t
     * @param _mask 求解本质矩阵时得到的内外点的标志位
     * @return
     */
     int recoverPose(*)

主要函数流程：relativePose()-->solveRelativeRT(求得E)-->recoverPose()[求得T]-->decomposeEssentialMat()[SVD分解]

5.GlobalSFM.construct

首先,将 feature 队列,放到 vector sfm_f 中,其中 SFMFeature 中的observation 存放的是观测到该路标点的 FrameId 及特征点坐标,如下所示:

GlobalSFM 的流程如下,其中,参考帧为上一步选出来的最共视帧,最后得到的sfm_tracked_points 为三角化出来的 3D 路标点。

几个主要的函数：

1.estimator.cpp–>initialStructure()–>construct():

/**initial_sfm.cpp
 * [GlobalSFM::construct description]
 * @param  frame_num          [滑窗内Frame个数]
 * @param  q                  [旋转量]
 * @param  T                  [平移量]
 * @param  l                  [共视帧的id]
 * @param  relative_R         now ===> l
 * @param  relative_T
 * @param  sfm_f              滑窗内所有的features
 * @param  sfm_tracked_points 三角化得到的points
 * @return
 * bool GlobalSFM::construct(*)
 */

2.estimator.cpp–>initialStructure()–>construct()–>solveFrameByPnP():

/**initial_sfm.cpp
 * [GlobalSFM::solveFrameByPnP PnP求解滑窗内关键帧的位姿]
 * @param  R_initial [description]  位姿，世界到相机坐标系
 * @param  P_initial [description]
 * @param  i         [description]
 * @param  sfm_f     [description]
 * @return           [description]
 */
bool GlobalSFM::solveFrameByPnP()

PnP(Perspective-n-Point)是求解3D到2D点对运动的方法.已知 $n$ 个空间点 $[X, Y, Z, 1]$ (前一帧的相机坐标系)以及他们的投影位置 $\left(u_{1}, v_{1}, 1\right)$ (归一化平面坐标系),使用直接线性变换(DLT)求解位姿。参考3D-2D:PnP_DLT.P3P。
$\left[\begin{array}{c}{u_{1}} \\ {v_{1}} \\ {1}\end{array}\right]=[R | t]_{3 * 4}\left[\begin{array}{l}{X} \\ {Y} \\ {Z} \\ {1}\end{array}\right]_{4 * 1}\tag{8}$

这个函数中主要的函数则是调用opencv的函数cv::solvePnP()调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法.对滑窗内每一帧图像,都跟上一步 SFM 得到的所有 3D 路标点,进行 cv::solvePnP 求解位姿。纯视觉初始化时,采用第一帧 $c_{0}$ 作为基准坐标系,若要转化为从 body 坐标系到 $c_{0}$ 坐标系,可以进行如下变换:
$q_{b_{k}}^{c_{0}}=q_{c_{k}}^{c_{0}} \otimes\left(q_{c}^{b}\right)^{-1}\tag{9}$ $s \overline{p}_{b_{k}}^{c_{0}}=s \overline{p}_{c_{k}}^{c_{0}}-R_{b_{k}}^{c_{0}} p_{c}^{b}\tag{10}$
上式推导如下,这里采用个人(崔神)较熟悉的写法:
$T_{c_{0} \leftarrow b_{k}}=T_{c_{0} \leftarrow c_{k}} T_{b \leftarrow c}^{-1}$ $\Leftrightarrow T_{c_{0}-b_{k}} T_{b \leftarrow c}=T_{c_{0} \leftarrow c_{k}}$ $\Leftrightarrow R_{c_{0} \leftarrow b_{k}}\left(R_{b \leftarrow c} P_{c_{k}}+t_{b \leftarrow c}\right)+t_{c_{0}-b_{k}}=R_{c_{0} \leftarrow c_{k}} P_{c_{k}}+t_{c_{0} \leftarrow c_{k}}\tag{11}$ $\Longrightarrow\left\{\begin{array}{c}{R_{c_{0} \leftarrow b_{k}}=R_{c_{0} \leftarrow c_{k}} R_{b \leftarrow c}^{-1}} \\ {t_{c_{0} \leftarrow b_{k}}=t_{c_{0} \leftarrow c_{k}}-R_{c_{0} \leftarrow b_{k}} t_{b \leftarrow c}}\end{array}\right.$

3.estimator.cpp–>initialStructure()–>construct()–>triangulateTwoFrames():

/**initial_sfm.cpp
 * [GlobalSFM::triangulateTwoFrames 三角化恢复出两帧共视的匹配点]
 * @param frame0 [特征帧1]
 * @param Pose0  [位姿1]
 * @param frame1 [特征帧2]
 * @param Pose1  [位姿2]
 * @param sfm_f  [特征点集合]   求取的点在世界坐标系
 */
void GlobalSFM::triangulateTwoFrames(*)

三角化这里详细推导过，求解过程和第二小节CalibrationExRotation相似，同样是使用奇异值分解求解超定方程的最小二乘解，至于奇异值的最小特征值对应的特征向量为什么是最小二乘的最优解也推导过，不再做笔记。同时这个函数主要是调用triangulatepoint()函数进行三角化：

/**
 * [GlobalSFM::triangulatePoint 三角化恢复特征点深度]
 * @param Pose0    [相机位姿1]
 * @param Pose1    [相机位姿2]
 * @param point0   [特征点1]
 * @param point1   [特征点2]
 * @param point_3d [恢复出的3D点]
 *
 *      求取的点在Pose0和Pose1的参考坐标系下
 *
 * |uP2-P0|
 * |vP2-P1|
 * |uQ2-Q0|P=0  参考ORB-SLAM初始化部分，DLT求解
 * |vQ2-Q1|
 * 解为矩阵P的最小奇异值对应的单位奇异矢量
 */
void GlobalSFM::triangulatePoint(*)

6.visualInitialAlign

这一节还有点蒙，懒得往上翻，再放一下这个图：在这里插入图片描述
IMU 预积分与视觉结构对齐示意图：

SFM 与 IMU 预积分结果对齐主要解决 3 个问题:

陀螺仪偏置的校准;
初始化速度、重力向量和尺度因子;
重力向量的精调。

estimator.cpp-->processImage()-->initialStructure()-->visualInitialAlign();

/**vins_estimator/src/initial/initial_aligment.cpp
 * [VisualIMUAlignment 视觉与IMU对齐，主要解决三个问题：
 *                     1) 修正陀螺仪的bias
 *                     2）初始化速度、重力向量g和尺度因子(Metric scale)
 *                     3）改进重力向量的量值]
 * @param  all_image_frame [包含图像特征和IMU预积分的集合]
 * @param  Bgs             [陀螺仪bias]
 * @param  g               [重力向量]
 * @param  x               [尺度因子]
 * @return                 [description]
 */
bool VisualIMUAlignment(*)

6.1.陀螺仪 bias 校正

estimator.cpp-->processImage()-->initialStructure()-->visualInitialAlign()-->solveGyroscopeBias();
考虑滑动窗口中的连续两个关键帧 $b_{k}$ 和 $b_{k+1}$ ,通过 SFM 可以获取两个关键帧时刻本体坐标系相对于参考相机坐标系的旋转 $q_{b_{k}}^{c_{0}}$ 和 $q_{b_{k+1}}^{c_{0}}$ ,通过 IMU 预积分可以获得两个关键帧时刻本体坐标系之间的相对旋转约束 $\gamma_{b_{k+1}}^{b_{k}}$ ,校正陀螺仪偏置的目标函数为:

$\min _{\delta b_{w}} \sum_{k \in B}\left\|q_{b_{k+1}}^{c_{0}-1} \otimes q_{b_{k}}^{c_{0}} \otimes \gamma_{b_{k+1}}^{b_{k}}\right\|^{2}\tag{12}$ 其中(一阶Taylor) $\gamma_{b_{k+1}}^{b_{k}} \approx \hat{\gamma}_{b_{k+1}}^{b_{k}} \otimes\left[\begin{array}{c}{1} \\ {\frac{1}{2} J_{\delta b_{k_{k}}}^{\delta \theta_{b_{k+1}}^{b_k}} \delta b_{w_{k}}}\end{array}\right]\tag{13}$
B 表示滑动窗口中的所有关键帧,等式(13)为 IMU 预积分中推导的, $\gamma_{b_{k+1}}^{b_{k}}$ 关于陀螺仪偏置误差 $\delta b_{w}$ 的一阶近似。

等式(12)中目标函数的最小值为单位四元数,所以可将等式(12)进一步改写为(这里的四元数采用实部在前,虚部在后的形式):
$q_{b_{k+1}}^{c_{0}-1} \otimes q_{b_{k}}^{c_{0}} \otimes \gamma_{b_{k+1}}^{b_{k}}=\left[\begin{array}{c}{1} \\ {0} \\ {0} \\ {0}\end{array}\right]$ $\hat{\gamma}_{b_{k+1}}^{b_{k}} \otimes\left[\begin{array}{c}{1} \\ {\frac{1}{2} J_{\delta b_{w_{k}}}^{\delta \theta_{b_{k+1}}^{b_k}} \delta b_{w_{k}}}\end{array}\right]=q_{b_{k}}^{c_{0}-1} \otimes q_{b_{k+1}}^{c_{0}} \otimes\left[\begin{array}{c}{1} \\ {0} \\ {0} \\ {0}\end{array}\right]\tag{14}$ $\left[\begin{array}{c}{1} \\ {\frac{1}{2} J_{\delta b_{k+1}}^{\delta \theta_{b_{k+1}}^{b_k}} \delta b_{w_{k}}}\end{array}\right]=\hat{\gamma}_{b_{k+1}}^{b_{k}-1} \otimes q_{b_{k}}^{c_{0}-1} \otimes q_{b_{k+1}}^{c_{0}} \otimes\left[\begin{array}{l}{1} \\ {0} \\ {0} \\ {0}\end{array}\right]$ 只考虑虚部,则有:

$J_{\delta b_{w_{k}}}^{\delta \theta_{b_{k+1}}^{b_k}}{\delta b_{w_k}}=2\left(\hat{\gamma}_{b_{k+1}}^{b_{k}-1} \otimes q_{b_{k}}^{c_{0}-1} \otimes q_{b_{k+1}}^{c_{0}}\right)_{v e c}\tag{15}$ 将等式(15)中等号坐标转为正定矩阵:
$[J_{\delta b_{w_{k}}}^{\delta \theta_{b_{k+1}}^{b_k}}]^TJ_{\delta b_{w_{k}}}^{\delta \theta_{b_{k+1}}^{b_k}}{\delta b_{w_k}}=2[J_{\delta b_{w_{k}}}^{\delta \theta_{b_{k+1}}^{b_k}}]^T\left(\hat{\gamma}_{b_{k+1}}^{b_{k}-1} \otimes q_{b_{k}}^{c_{0}-1} \otimes q_{b_{k+1}}^{c_{0}}\right)_{v e c}\tag{16}$
这样就可以使用 cholesky 分解求解矩阵(16),获取目标函数达到最小的解 $\delta b_{w}$ ,从而完成对陀螺仪偏置的校正。

/**
 * [solveGyroscopeBias description]
 * @param  all_image_frame [包含图像特征和IMU预积分的集合]
 * @param  Bgs             [陀螺仪bias]
 * 这部分可以参考文献[1]中公式(15)部分(注：'表示求逆)
 *
 * Min sum||q_cb1' × q_cb0 × r_bkbk+1||      (1)
 * 
 * 公式(15)的最小值是1(q(1,(0,0,0)，所以将其前半部分移到右边得
 *            |     1   |
 * r_bkbk+1^ ·| 1/2·J·bw|=q_cb0' q_cb1        (2)
 *
 *            |     1   |
 *            | 1/2·J·bw|=r_bkbk+1^' × q_cb0' × q_cb1        (3)
 * 
 * 只取四元数的虚部并求解，
 *            JTJ·bw = 2JT(r_bkbk+1^' × q_cb0' × q_cb1).vec  (4)
 * 即，A·bw=b，将多个帧综合起来为
 *            sum(A)bw = sum(b)                              (5)
 */

//gyro的标定思路是:对于相邻的两帧, vision有一个相对旋转q, IMU预积分有一个相对旋转γ, Align的目的就是寻找一个最好的δbw使得两个相对旋转尽可能接近
void solveGyroscopeBias(map<double, ImageFrame> &all_image_frame, Vector3d* Bgs)

6.2.初始化速度、重力和尺度因子

estimator.cpp-->processImage()-->initialStructure()-->visualInitialAlign()-->LinearAlignment(×);
这一部分的内容对应于 VINS-Mono 代码 initial_aligment.cpp 中的 LinearAlignment()函数。待优化的变量为:
$\chi_{I}=\left[\begin{array}{c}{v_{b_{0}}^{b_{0}}} \\ {v_{b_{0}}^{b_{0}}} \\ {\vdots} \\ {v_{b_{0}}^{b_{0}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right]\tag{17}$
将预积分项中的世界坐标系 $w$ 换为 $c_0$ 坐标系:
$\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(p_{b_{k+1}}^{c_{0}}-p_{b_{k}}^{c_{0}}-v_{b_{k}}^{c_{0}} \Delta t_{k}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}\right)\tag{18}$ $\beta_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(v_{b_{k+1}}^{c_{0}}-v_{b_{k}}^{c_{0}}+g^{c_{0}} \Delta t_{k}\right)\tag{19}$
$p_{b_{k+1}}^{c_{0}}$ 和 $p_{b_{k}}^{c_{0}}$ 可由视觉 SFM 获得:
$p_{b_{k}}^{c_{0}}=s \overline{p}_{b_{k}}^{c_{0}}\tag{20}$ $p_{b_{k+1}}^{c_{0}}=s \overline{p}_{b_{k+1}}^{c_{0}}\tag{21}$ 将等式(20)(21)代入等式(18):
$\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{c}}\left(s\left(\overline{p}_{b_{k+1}}^{c_{0}}-\overline{p}_{b_{k}}^{c_{0}}\right)-v_{b_{k}}^{c_{0}} \Delta t_{k}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}\right)\tag{22}$ 将等式(19)(22)中的速度都转换到 $c_0$ 坐标系下:
$\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(s\left(\overline{p}_{b_{k+1}}^{c_{0}}-\overline{p}_{b_{k}}^{c_{0}}\right)-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}} \Delta t_{k}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}\right)\tag{23}$ $\beta_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(R_{b_{k+1}}^{c_{0}} v_{b_{k+1}}^{b_{k+1}}-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}}+g^{c_{0}} \Delta t_{k}\right)\tag{24}$ 想办法将等式(23)(24)转换成 $H x=b$ 的形式,这样便于利用 cholesky 进行求解。将等式(10)带入等式(23):

$\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(s\left(\overline{p}_{b_{k+1}}^{c_{0}}-\overline{p}_{b_{k}}^{c_{0}}\right)-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}} \Delta t_{k}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}\right) \Rightarrow$

$\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(\left(s \overline{p}_{c_{k+1}}^{c_{0}}-R_{b_{k+1}}^{c_{0}} p_{c}^{b}\right)-\left(s \overline{p}_{c_{k}}^{c_{0}}-R_{b_{k}}^{c_{0}} p_{c}^{b}\right)-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}} \Delta t_{k}+\frac{1}{2} g^{c_{0}} \Delta t_{k}^{2}\right) \Rightarrow$

$\alpha_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}} s\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{b_{0}}\right)-R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}+p_{c}^{b}-v_{b_{k}}^{b_{k}} \Delta t_{k}+\frac{1}{2} R_{c_{0}}^{b_{k}} g^{c_{0}} \Delta t_{k}^{2} \Rightarrow$
$\tag{25}$
$-v_{b_{k}}^{b_{k}} \Delta t_{k}+\frac{1}{2} R_{c_{0}}^{b_{k}} g^{c_{0}} \Delta t_{k}^{b_{k}}\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{c_{0}}\right) s=\alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b} \Rightarrow$

$\left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2}} & {R_{c_{0}}^{b_{k}}\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{c_{0}}\right)}\end{array}\right]\left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right]=\alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}$

同样地也将等式(24)转换为矩阵形式:

$\beta_{b_{k+1}}^{b_{k}}=R_{c_{0}}^{b_{k}}\left(R_{b_{k+1}}^{c_{0}} v_{b_{k+1}}^{b_{k+1}}-R_{b_{k}}^{c_{0}} v_{b_{k}}^{b_{k}}+g^{c_{0}} \Delta t_{k}\right) \Rightarrow$

$-v_{b_{k}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} v_{b_{k+1}}^{b_{k+1}}+R_{c_{0}}^{b_{2}} g^{c_{0}} \Delta t_{k}=\beta_{b_{k+1}}^{b_{k}} \Rightarrow$
$\tag{26}$
$\left[\begin{array}{cccc}{-I } & {R_{c_0}^{b_k}R_{c_0}^{b_{k+1}} } & { R_{c_{0}}^{b_{k}} \Delta t_{k}} & {0}\end{array}\right]\left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right]=\beta_{b_{k+1}}^{b_{k}}$

联立等式(25)(26):
$\left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{x}} \Delta t_{k}^{2}} &{R_{c_{0}}^{b_{k}}\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{c_{0}}\right)} \\ {-I} & {R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}}} & {R_{c_{0}}^{b_{k}} \Delta t_{k}} &{0} \end{array}\right] \left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right]=\left[\begin{array}{c}{\alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}} \\ {\beta_{b_{k+1}}^{b_{k}}}\end{array}\right]\tag{27}$
理论上等式(27)中的等号应该成立,但是由于各种噪声与数值运算的误差,等号并不严格成立,将理论真值 $\alpha_{b_{k+1}}^{b_{k}}, \beta_{b_{k+1}}^{b_{k}}$ 替换为通过 IMU 测量值计算出的标称值 $\hat{\alpha}_{b_{k+1}}^{b_{k}}, \hat{\beta}_{b_{k-1}}^{b_{k}}$ 得到约等式:

$\left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{x}} \Delta t_{k}^{2}} &{R_{c_{0}}^{b_{k}}\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{c_{0}}\right)} \\ {-I} & {R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}}} & {R_{c_{0}}^{b_{k}} \Delta t_{k}} &{0} \end{array}\right] \left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right] \approx \left[\begin{array}{c}{\alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}} \\ {\beta_{b_{k+1}}^{b_{k}}}\end{array}\right]\tag{28}$

令：
$H_{b_{k+1}}^{b_{k}}=\left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{x}} \Delta t_{k}^{2}} &{R_{c_{0}}^{b_{k}}\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{c_{0}}\right)} \\ {-I} & {R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}}} & {R_{c_{0}}^{b_{k}} \Delta t_{k}} &{0} \end{array}\right]\tag{29}$

$\chi_{b_{k+1}}^{b_{k}}=\left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ {g^{c_{0}}} \\ {s}\end{array}\right]\tag{30}$

$\hat{z}_{b_{k+1}}^{b_{k}}=c\left[\begin{array}{c}{\alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}} \\ {\beta_{b_{k+1}}^{b_{k}}}\end{array}\right]\tag{31}$

约等式(28)可简写为:
$H_{b_{k+1}}^{b_{k}} \chi_{b_{k+1}}^{b_{k}} \approx \hat{z}_{b_{k+1}}^{b_{k}}\tag{32}$
通过解线性最小二乘问题:
$\min _{\chi_{b_{k+1}}^{b_{k}}} \sum_{k \in B}\left\|\hat{z}_{b_{k+1}}^{b_{k}}-H_{b_{k+1}}^{b_{k}} \chi_{b_{k+1}}^{b_{k}}\right\|^{2}\tag{33}$
即可优化 $\chi_{I}$ ,即滑动窗口中所有关键帧的速度、重力向量在 $c_0$ 坐标系中的分量列阵和单目尺度因子 $s$ 。

/**
 * [LinearAlignment 初始化速度、重力向量g和尺度因子(Metric scale)]
 * @param  all_image_frame [包含图像特征和IMU预积分的集合]
 * @param  g               [重力向量]
 * @param  x               [description]
 * @return                 [description]
 * 参考
 */
bool LinearAlignment(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)

6.3.修正重力矢量

对应代码中 vins_estimator/src/initial/initial_aligment.cpp-->RefineGravity()函数.

假设重力的模值固定,且其数值为已知量,这样重力向量的自由度就由 3 变成了 2。因此将重力向量重新参数化:重力矢量的模长固定(9.8),其为 2 个自由度,在切空间上对其参数化:
$\begin{aligned} \hat{g} &=\|g\| \overline{\hat{g}}+w_{1} b_{1}+w_{2} b_{2} \\ &=\|g\| \overline{\hat{g}}+\left[\begin{array}{cc}{b_{1}} & {b_{2}}\end{array}\right]\left[\begin{array}{c}{w_{1}} \\ {w_{2}}\end{array}\right] \\ &=\|g\| \overline{g}+b w \end{aligned}$ 既是：
$\begin{aligned} \hat{g} &=\|g\| \cdot \overline{\hat{g}}+\omega_{1} \overrightarrow{b_{1}}+\omega_{2} \overrightarrow{b_{2}} \\ &=\|g\| \cdot \hat{\hat{g}}+\vec{B} \vec{\omega} \end{aligned}, \quad B \in \mathbb{R}^{3 \times 2}, \vec{\omega} \in \mathbb{R}^{2 \times 1}\tag{34}$
$\overline{\hat{g}}$ 为重力向量的方向向量在 $\mathcal{C}_{0}$ 坐标系下的坐标, $b_{1}, b_{2}$ 为重力向量正切空间的一对正交基。重新参数化后的重力向量由 $\omega$ 控制。令 $\hat{g}=g^{c_{0}}$ 代入公式(28)得:
$\left[\begin{array}{cccc}{-I \Delta t_{k}} & {0} & {\frac{1}{2} R_{c_{0}}^{b_{x}} \Delta t_{k}^{2}} &{R_{c_{0}}^{b_{k}}\left(\overline{p}_{c_{k+1}}^{c_{0}}-\overline{p}_{c_{k}}^{c_{0}}\right)} \\ {-I} & {R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}}} & {R_{c_{0}}^{b_{k}} \Delta t_{k}} &{0} \end{array}\right] \left[\begin{array}{c}{v_{b_{k}}^{b_{k}}} \\ {v_{b_{k+1}}^{b_{k+1}}} \\ { \omega } \\ {s}\end{array}\right]$
$= \left[\begin{array}{c}{\alpha_{b_{k+1}}^{b_{k}}-p_{c}^{b}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-\frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2}\|\mathrm{g}\| \cdot \overline{\mathbf{g}}} \\ {\beta_{b_{k+1}}^{b_{k}}-R_{c_{0}}^{b_{k}} \Delta t_{k}\|\mathrm{g}\| \cdot \overline{\widehat{\mathrm{g}}}}\end{array}\right]\tag{35}$

即: $H^{6 \times 9} X_{I}^{9 \times 1}=b^{6 \times 1}, \quad \omega^{2 \times 1}=\left[\omega_{1}, \omega_{2}\right]^{T}$ 这样,可以用 Cholosky 分解下面方程求解 $X_{I}$ : $H^{T} H X_{I}=H^{T} b\tag{35}$
同样通过 Cholosky 分解求得 $g^{c_{0}}$ ,即相机 $C_0$ 系下的重力向量。最后,通过将 $g^{c_{0}}$ 旋转至惯性坐标系(世界系)中的 z 轴方向 [0,0,1],可以计算第一帧相机系到惯性系的旋转矩阵 $q_{c_{0}}^{w}$ ,这样就可以将所有变量调整至惯性世界系(水平坐标系,z 轴与重力方向对齐)中。

/**vins_estimator/src/initial/initial_aligment.cpp
 * [RefineGravity 纠正重力向量和速度]
 * @param all_image_frame [description]
 * @param g               [description]
 * @param x               [description]
 */
//每次估计完g以后, 都会做一次归一化使得其模值为G, 所以可以理解为这里的refine其实是refine重力的方向, 同时refine其他估计量. 
//因为方向基本不会差太多, w1,w2通常很小, 所以可以做这样的近似.
void RefineGravity(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)