L1正则化与稀疏性、L1正则化不可导问题

转：L1正则化与稀疏性

坐标轴下降法（解决L1正则化不可导的问题）、Lasso回归算法： 坐标轴下降法与最小角回归法小结

L1正则化使得模型参数具有稀疏性的原理是什么？

机器学习经典之作《pattern recognition and machine learning》中的第三章作出的一个解释无疑是权威且直观的，我们也经常都是从这个角度出发，来解释L1正则化使得模型参数具有稀疏性的原理。再回顾一下，以二维为例，红色和黄色的部分是L1、L2正则项约束后的解空间，蓝色的等高线是凸优化问题中的目标函数（未加入正则项的）的等高线，如图所示，L2正则项约束后的解空间是圆形，而L1正则项约束后的解空间是菱形，显然，菱形的解空间更容易在尖角处与等高线碰撞出稀疏解。

假设原目标函数是 $y=(w_1−2)^2+(w_2−2)^2$

在未加入正则项之前，这个最优解无疑是 $（w_1=2，w_2=2）$
但加入了正则项 $y=(w_1−2)^2+(w_2−2)^2+1∗（w^2_1+w^2_2）$
之后但最优解就不再是 $（w_1=2，w_2=2）$而是 $（w_1=1，w_2=1）$
这是 $(w_1−2)^2+(w_2−2)^2=a$ 和 $w^2_1+w^2_2=b$这两个圆的切点。切点处 $a=2,b=2$,此时正好 $a=b$，这与我们的目标函数取值 $y=(w_1−2)^2+(w_2−2)^2$ 是个圆形有关，如果是其他形状，不一定有 $a=b$。

上面的解释无疑是正确的，但还不够准确，也就是回答但过于笼统，以至于忽略了几个关键问题，例如，为什么加入正则项就是定义了一个解空间约束，为什么L1、L2正则项的解空间不同。如果第一个问题回答了，第二个问题相对好回答。
其实可以通过kkt条件给出一种解释。

事实上，“带正则化项”和“带约束条件”是等价的，为了约束w的可能取值空间从而防止过拟合。

如果我们为线性回归加上一个约束，就是 $w$ 的 $l2$ 范数不能大于 $m$ :

为了求解这个带约束条件的不等式，我们会写出拉格朗日函数
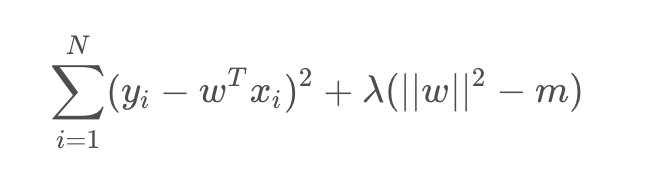如果w∗w^{}w
∗
是原问题(1)的解,λ∗\lambda^{}λ
∗
是对偶问题(2)的解,
一般都是先求出对偶问题的解λ∗\lambda^{}λ
∗
,然后带入kkt条件中（λ∗\lambda^{}λ
∗
和w∗w^{}w
∗
的关系），就能求出w∗w^{}w
∗
。w∗w^{*}w
∗
也必然是原问题的解。
这里kkt条件是：

其中，第一个式子就是带L2正则项的优化问题最优解w∗w^{}w
∗
，而λ∗\lambda^{}λ
∗
是L2正则项前的系数。

这就是为什么带正则化项相当于为参数约束了解空间，且L2正则项为参数约束了一个圆形解空间，L1正则项为参数约束了一个菱形解空间，如果原问题的最优解没有落在解空间的内部，就只能落在解空间的边界上。
而L1正则项为参数约束了一个“棱角分明”的菱形解空间，更容易与目标函数等高线在角点，坐标轴上碰撞，从而产生稀疏性。

看到上面，其实我直接有个疑问，就是“如果我们为线性回归加上一个约束，就是w的l2范数不能大于m”、这句话里的m是个固定的确定值，还是瞎设的值。
后面我的想法是，任意给定一个m值，都能得到一个两圆相切的切点，从而得到其给定m条件下的带正则项的最优解，然后在不同的m值中，再选出某个m值对应的最优解是全局最优解，从而得到最终的最优解。