快速排序真的没你想的那么难

前言:
作为一名程序猿，大家应该或多或少都听过快速排序的大名，可能很多小伙伴最初接触到快排的时候是在数据结构的课上。当时课上可能恍恍惚惚的听懂了，但是后面又没下来继续钻研，就又把这个知识点还回去了，其实快排真的没有想象中的那么难，本文将先从思路较为简单的递归入手，然后再利用非递归的方式实现快速排序。好了，进入今天的主题吧。

一、快速排序的原理

• 分区
  分区是快排中一个非常重要的环节，快排将从数组中间位置作为分界线，将整个数组分成两个分区，前一个分区中每个元素的值小于原来数组中间位置上的值，后一个分区中每个元素的值大于原数组中间位置上的值。（需要注意的是我们这里所说的中间位置仅仅是数组下标为中间位置所对应的数组的值）。
  举个例子吧：
  比如我们有一个数组 $array=[4,2,5,9,6,3,1,8,7]$
  现在对他分区，我们知道这个属组的长度为 9 ，那么现在中间位置的下标可以这样计算$\lfloor 9/2\rfloor =4$ (注意取整是取得下限)我们再来看数组对应位置得值 $array[4]=6$ (数组的下标是 0 开始的) ,那么现在我们标记上这个中间值。
  $$array=[4,2,5,9,\overline{(6)},3,1,8,7]$$
  现在以标记元素为界，然后将其他的元素与这个标记值比较，比它大就放在后面的分区，比它小就放在前面的分区。
  $$[4,2,5,3,1],\overline{(6)},[9,8,7]$$
  你可以看到即便我们分了区，但是每个分区内部相较于原来的数组各个元素之间的相对位置是没有改变的。
  通过分区之后我们就得到了下面两个分区：
  $$\{\begin{array}{l}[4,2,5,3,1]\\ [9,8,7]\end{array}$$
  不妨我们现在人工先对这个两个分区进行排序看看：
  $$\{\begin{array}{l}[1,2,3,4,5]\\ [7,8,9]\end{array}$$
  排序完成之后我们再返回原来的分区数组中来看：
  $$[1,2,3,4,5],\overline{(6)},[7,8,8]$$
  很惊讶的发现竟然全局都已经有序了，其实不必惊讶应为这是必然的现象，因为我们要使整个数组有序那必然比中间值小的元素再中间位置前面的分区，比中间值大的再数组有序后必然会在中间值的后面的分区，如果不是必然是不成立的。
  证明：
  假设 $[a,b,c]$ 已经是正序数组（也就是从下达到有序），
  现在打乱对 $[c,a,b]$ 排序。
  如果分区后为: $[b,a,c]$
  显然是跟我们前面的假设是冲突的，因为 $b>a$

• 重复使用快排思想
  不知道大家发现没有，我们前面的步骤对原数组分完区后是自己手动对每个分区中的元素进行排序的，如果快排就这样结束了，那又和其他的排序算法有什么区别呢。聪明的小伙伴应该也想到了，既然对分区也是排序，何不将分区再看成一个独立的数组，然后对这个数组再采用快速排序呢？让我们来看看：
  这次我们用图片来表示整个流程
  
  可以看到我们使用快排可以很快的就完成对无序的数组排序，图中有颜色的行代表分区的过程。

  二、使用递归实现快排算法

  • 其实根据我们上面分析的整个快排的过程，你应该可以很容易的就利用递归来实现这个算法，为什么呢？你想我们不断的在给数组分区，又不断的又把分区的数组再次使用快排算法，难道这还不是递归吗，既然是递归那么肯定就是有套路的啦。
    第一步寻找递归表达式：
    $$qsort(arr)=[qsrot(less),arr[qivot],qsort(greater)]$$
    表达式根据分析很容易写出，其中 qsort() 代表快排函数，less 代表 arra 的前面一个分区（数值较小）， greater 代表后面一个分区（数值较大），qivot 代表中arr的中间位置的下标。
    第二步就是找到递归的跳出条件：
    根据常识就可以知道，当数组的长度为 1 或 0 时我们是不用排序的吧，那这就是我们的递归跳出条件：
    i f ( a r r . s i z e ( ) < 2 ) { r e t u r n   a r r } ; if(arr.size() < 2)\{return \ arr\}; if(arr.size()<2){ return arr};
    有了这两个线索，我们就可以来实现递归方式的快排了：

    #include<iostream>
    #include<vector>
    
    using namespace std;
    
    vector<int> qsort(vector<int> arr){
            
            
        if(arr.size() < 2){
            
            
            return arr;
        }
        // 计算中间位置的下标
        int qivot = arr.size()/2;
        // 记录中间位置对应的值
        int m = arr[qivot];
        // 从数组中删除中间位置的值
        arr.erase(arr.begin() + qivot);
        vector<int> less,greater;
        // 开始分区
        for(int n:arr){
            
            
            if(n < m){
            
            
                // 比中间值小的加入小值分区末尾
                less.push_back(n);
            }
            else{
            
            
                // 比中间值大或者等于的加入大值分区尾部
                greater.push_back(n);
            }
        }
        // 递归调用 对小值分区排序
        less = qsort(less);
        // 递归调用 对大值分区排序
        greater = qsort(greater);
    
        // 合并数组并返回  less + m + greater
        less.push_back(m);
        less.insert(less.end(),greater.begin(),greater.end());
        return less;
    }
    
    int main(){
            
            
        vector<int> a = {
            
            4,2,5,9,6,3,1,8,7};
        a = qsort(a);
        for(int n:a){
            
            
            cout << n << '\t';
        }
    }
    

• 这里为了尽量满足上面我们分析的思路，所以代码逻辑很简单，思路完全就是我们上面所分析的思路（其实这样做效率是非常低下的，因为空间上开销会非常大，但是初学者看着更容易明白，也更容易看懂这个代码的逻辑。如果要改进可以使用两个下标的方式来表示数组的某一段，或者也叫分区，这里就不多说了）。代码只实现了从小到大的排序，小伙伴们不妨自己再实现一遍从大到小的快速排序，也好检验自己是否已经真正掌握了。

三、非递归方式实现(拓展)*

• 代码仅供参考：

  #include<iostream>
  #include<vector>
  #include<stack>
  
  using namespace std;
  
  int partition(vector<int> &arr,int low,int high){
        
        
      int qivot_value = arr[low];
      while(low < high){
        
        
          while(low < high && arr[high] >= qivot_value) high--;
          arr[low] = arr[high];
          while(low < high && arr[low] <= qivot_value) low++;
          arr[high] = arr[low];
      }
      arr[low] = qivot_value;
      return low;
  }
  
  void qsort(vector<int> &arr,int low,int high){
        
        
       stack<int> s;
      if (low< high)
      {
        
        
          int mid = partition(arr, low, high);
          if (mid-1>low)
          {
        
        
              s.push(low);
              s.push(mid - 1);
          }
          if (mid+1<high)
          {
        
        
              s.push(mid + 1);
              s.push(high);
          }
  
          while (!s.empty())
          {
        
        
              int q_high = s.top();
              s.pop();
              int p_low = s.top();
              s.pop();
              int pq_mid = partition(arr, p_low, q_high);
              if (pq_mid - 1 > p_low)
              {
        
        
                  s.push(p_low);
                  s.push(pq_mid - 1);
              }
              if (pq_mid + 1 < q_high)
              {
        
        
                  s.push(pq_mid + 1);
                  s.push(q_high);
              }
          }
  
      }
  }
  
  int main(){
        
        
      vector<int> a = {
        
        4,2,5,9,6,3,1,8,7};
      qsort(a,0,8);
      for(int n:a){
        
        
          cout << n << '\t';
      }
  }
  

其实非递归的实现方式也不过就是模拟递归的原理，我们使用自定义的一个栈来手动模拟函数调用栈的过程，这样是得不偿失的，因为语言内部已经对函数栈进行了优化的，我们自己实现的这个栈必然是没有内部函数栈那么高效，但是我们这样做也有一个好处就是不会出现栈溢出问题。我们都知道函数栈再调用到一定的层数时就会栈溢出，然而我们自己模拟实现函数栈的这个代码就不会出现这样的情况，如果要选择使用递归方式，还是非递归方式看自己吧，权衡利弊关系；

四、时间复杂度分析

• 通过递归代码的执行流程，我们来分析快速排序的时间复杂度；
  
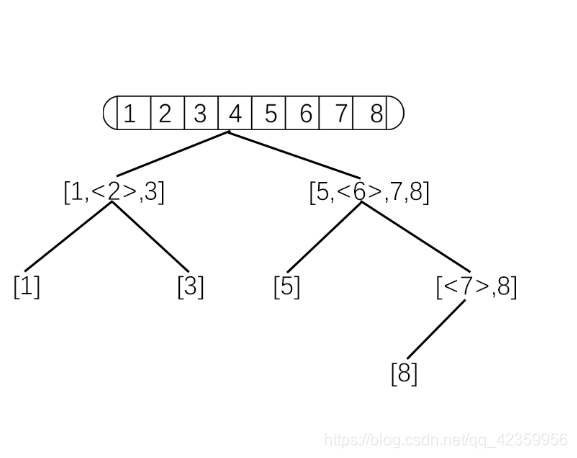
  每一层的时间复杂度为$o(n)$，然后递归的层数刚好就是 log8=3,所以快排一般的时间复杂度就是
  $$o(n)\ast o(logn)=o(nlogn)$$
  ,但是快排有一种最坏的情况，请看：
  
  在这种情况下我们数据严重倾斜到一边（注意这里我们每次时选取第一位作为qivot，所以和前面递归时讲得有点偏差），很明显这时层数为 n 层，那么此时的时间复杂度就为$o(n)\ast n=o(n^2)$,但是快排的平均时间复杂度还是$o(nlogn)$,相比冒泡排序，选择排序还是快了很多，其实快排还有很多优化，比如，三数取中，插排，聚集相等元素等等优化，如果有兴趣的小伙伴就可以进一步探究。