此笔记对应的B站视频:
https://www.bilibili.com/video/BV1854y1D7dy
https://www.bilibili.com/video/BV1op4y1Q7yu
文章目录
动态性能介绍
上升时间 t r t_{r} tr
- 指响应从终值的10%上升到终值的90%所需的时间(亦可定义为响应从0第一次上升到终值所需的时间)
- 有的过阻尼系统终值不到100%,所以算的是从终值的10%上升到终值的90%所需的时间
- 上升时间越短,响应速度越快
峰值时间 t p t_{p} tp
- 指响应超过其终值到达第一个峰值所需的时间。
- 体现系统的响应速度。
调节时间 t s t_{s} ts
- 指响应到达并保持在终值 ± 5 % \pm5\% ±5%或 ± 2 % \pm2\% ±2%内所需的最短时间。
超调量 σ % \sigma\% σ%
- 指响应的最大偏离量与终值之差与终值比的百分数,即
σ % = h ( t p − h ( ∞ ) ) h ( ∞ ) × 100 \sigma\%=\frac{h(t_{p}-h(\infty))}{h(\infty)}\times100% σ%=h(∞)h(tp−h(∞))×100
小结
- 通常以上升时间和峰值时间评价系统的响应速度
- 以超调量评价系统的阻尼程度
- 调节时间是反映响应速度和阻尼程度的综合性能指标
稳态性能介绍
- 稳态误差是描述系统稳态性能的一种性能指标,通常在阶跃函数、斜坡函数或加速度函数作用下进行测定或计算。
- 若时间趋于无穷时,系统的输出量不等于输入量或输入量的确定函数,则系统存在稳态误差。
- 稳态误差是系统控制精度或抗扰动能力的一种度量。
稳不稳,快不快,看动态性能;准不准,看稳态性能。
线性系统的稳定性分析
1. 稳定性的概念和定义
- 线性控制系统的稳定性定义:设线性控制系统在初始扰动 f ( t ) f(t) f(t)的影响下其过渡过程随时间的推移逐渐衰减并趋向于零,则称该系统为稳定。
- 不稳定:若在初始扰动 f ( t ) f(t) f(t)的影响下系统过渡过程随时间的推移而发散,则称该系统为不稳定。
2. 稳定系统的充要条件
- 脉冲系统的脉冲响应(输入为脉冲时的输出)
- 系统稳定 ⟺ \iff ⟺特征根均具有负实部
临界稳定不算稳定。
3. 稳定判据(代数判据)
(1) Hurwitz稳定判据
- 系统稳定的必要条件:特征方程式各项系数符号相同,且均不为0。
- 如下图,因为系数-6,所以不稳定。
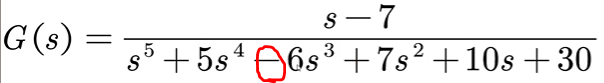
- 如下图,因为少了 s 3 s^3 s3项,即该项系数为0,所以不稳定。
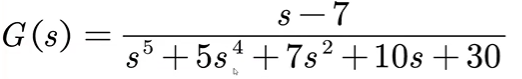
- 如下图,因为系数-6,所以不稳定。
- 系统稳定的充要条件:各阶Hurwitz行列式 D i ( i = 1 , 2 , . . . , n ) D_{i}(i=1,2,...,n) Di(i=1,2,...,n)全大于零。
(2) LIENARD-CHIPARD稳定判据
- 若特征方程式所有系统同符号且均不为零,如果所有奇次阶Hurwitz行列式为正,则所有偶次阶Hurwitz行列式亦必为正。反之亦然。
- 林纳德-奇帕特稳定判据(充要条件为):
- A:系统特征方程式各项系数符号相同。且均不为零;
- B:奇数阶(或偶数阶)Hurwitz行列式均大于零。
(3) Routh稳定判据
-
Routh稳定判据的充要条件为:
- A:特征方程式的全部系数均具有相同符号,且均不为0
- B:劳斯表中第一列各元素的值都大于0
-
Routh稳定判据的说明:
- 若第一列元素值出现小于0的数值,系统不稳定
- 第一列元素符号改变的次数,就是系统特征方程的正实部(右)根的数目
-
Routh判据的两种特殊情况
- A:劳斯表中某一行中第一个元素为0,而其余不全为0
- 处理方法1:用因子 ( s + a ) (s+a) (s+a)乘以原特征方程(a为任意正数),然后对新特征方程用劳斯判据判断。
- 处理方法2:用一个小正数 ε \varepsilon ε代替0,然后将计算进行下去。
- B:劳斯表的某一行的元素全部为0(如果该行只有一个元素且为0,则按全零行处理)
- 原因:系统特征方程存在一些大小相等、符号相反的根
- 处理方法:
- 用全零行的上一行的元素为系数构造一个辅助方程(解辅助方程可以求得系统不稳定的根);
- 对辅助方程求导;
- 用求导后所得的方程的系数代替全零行元素;
- 继续计算。
- A:劳斯表中某一行中第一个元素为0,而其余不全为0
-
强调指出
- A:当系统特征方程式各项系数符号不相同或特征方程有零系数时系统不稳定;
- B:当劳斯表中出现两种特殊情况时,系统不稳定;
- C:辅助方程可用于求取系统的部分不稳定根。
-
当已知线性系统的特征方程时,应用代数判据可以
- A:分析判断系统的稳定性;
- B:分析系统参数变化对系统稳定性的影响(参数取值范围、临界增益);
- C:确定系统的相对稳定性。
例6:系统的特征方程为 s 4 + s 3 − 3 s 2 − s + 2 = 0 s^4+s^3-3s^2-s+2=0 s4+s3−3s2−s+2=0,试判断系统的稳定性。
解:

注意: s 1 s^1 s1这一行的第一个元素为0,不应按第一种特殊情况处理,而应按第二种特殊情况全零行处理。

例7:已知系统的特征方程为 s 3 + 2 s 2 + s + 2 = 0 s^3+2s^2+s+2=0 s3+2s2+s+2=0,试判断系统的稳定性。
解:

4. 代数判据的应用
(1) 系统参数变化对系统稳定性的影响
(2) 确定系统的相对稳定性——稳定裕度
例10:
要使[例10]系统闭环特征根全部位于[s]平面的s=-1垂涎以左,K的取值范围是什么?

解:


一阶系统的时域分析
1. 一阶系统的数学模型
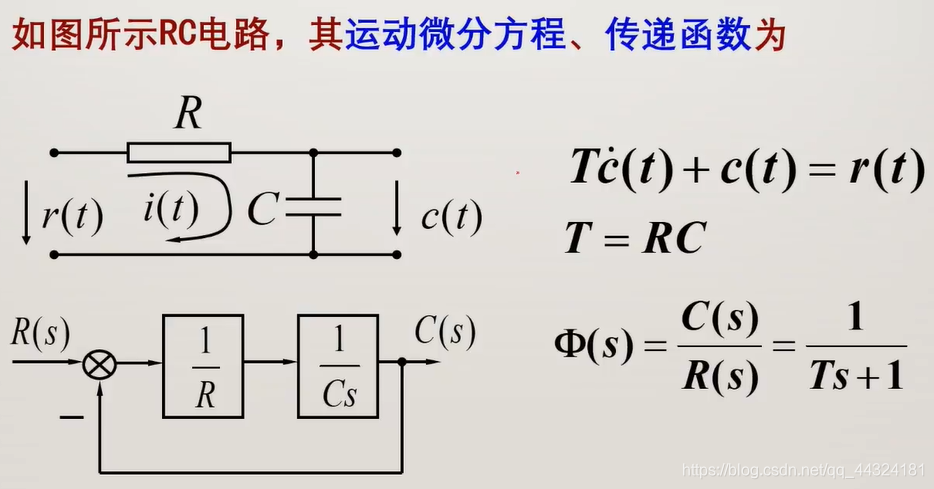
线性定常系统时域分析方法(回顾)

典型输入信号(回顾)

2. 一阶系统的单位脉冲响应


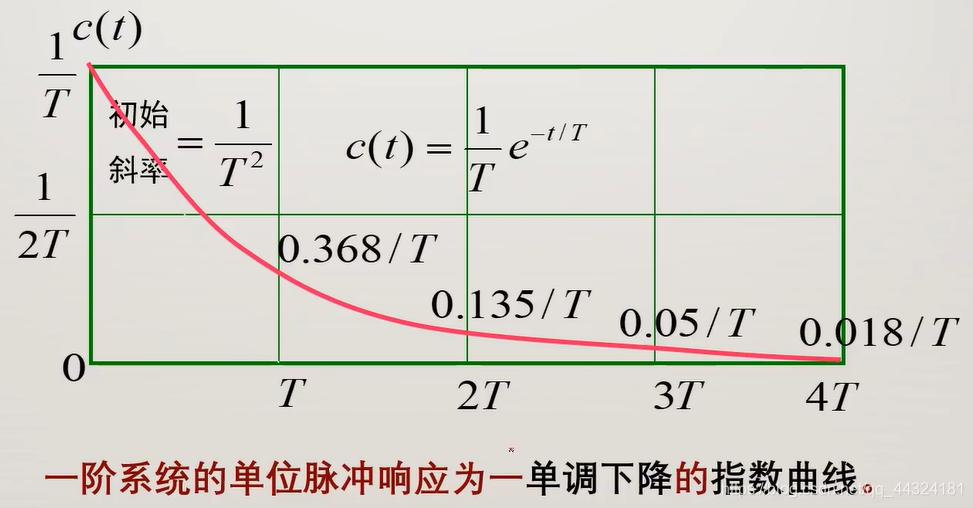
3. 一阶系统的单位阶跃响应


输出是单调收敛至1的,可以求t=0和 t = ∞ t=\infty t=∞时的值,求导发现导数是正数,故单调。
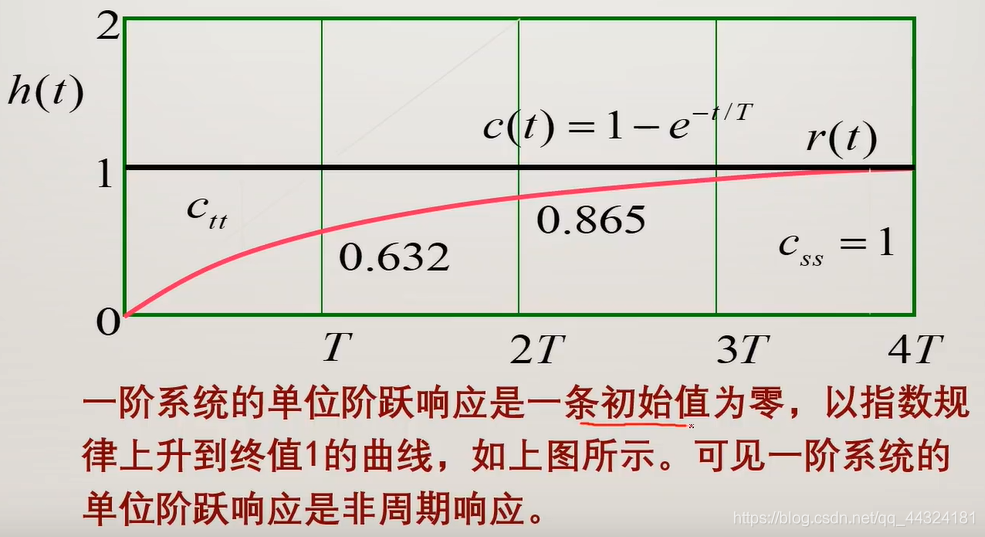
一阶系统的动态性能指标

4. 一阶系统的单位斜坡响应


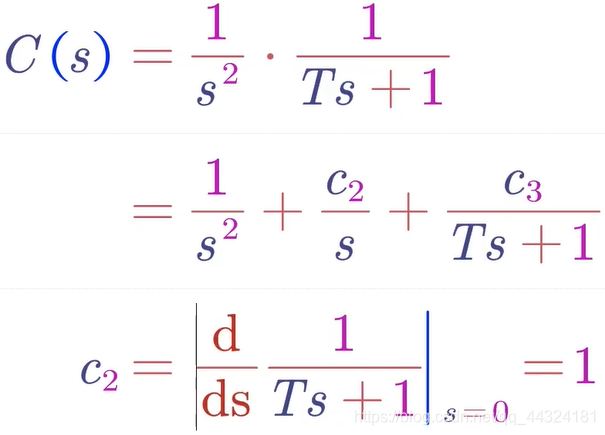
- 输入斜坡函数之后,系统的输出与输入间的误差会趋于一个定值 − T -T −T。
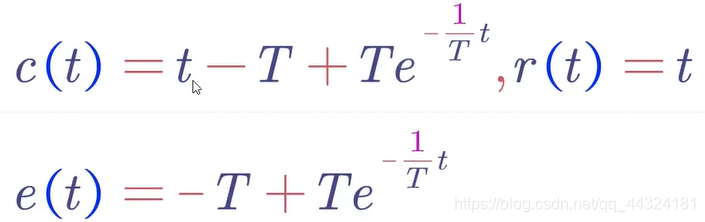
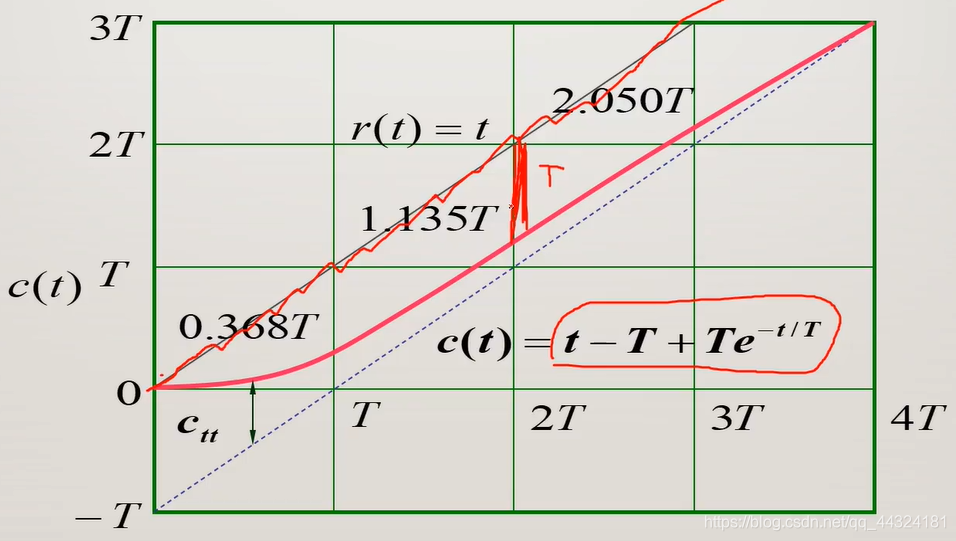
- 一阶系统的单位斜坡响应的稳态分分量,是一个与输入斜坡函数斜率相同,但时间滞后 T T T的斜坡函数,位置上存在稳态跟踪误差,其值为时间常数 T T T。
- 一阶系统的瞬态分量为衰减非周期函数。
- 在斜坡响应曲线中,输出量与输入量间的位置误差随时间而增大,并趋于常值 T T T。
5. 一阶系统的单位加速度响应

- 输入加速度函数之后,系统的输出与输入间的误差会发散至无穷大。
- 所以,系统的跟踪误差为
e ( t ) = r ( t ) − c ( t ) = T t − T 2 ( 1 − e − t T ) e(t)=r(t)-c(t)=Tt-T^2(1-e^{-\frac{t}{T}}) e(t)=r(t)−c(t)=Tt−T2(1−e−Tt) - 上式表明,跟踪误差随时间的推移而增大,直至无限大。说明一阶系统不能实现对加速度输入函数的跟踪。
6. 小结:一阶系统对典型输入信号的输出响应


- 阶跃信号的输出与输入的误差趋于0。
- 斜坡信号的输出与输入误差趋于常数 T T T。
- 加速度信号的输出与输入的误差趋于无穷大。
下一篇:二阶系统的时域分析