前言

近世代数中群、环、域的定义都是基于集合的，通过对集合上运算的约束，将集合构造成具有不同特性的新对象。

集合：具有共同属性的事物的总体。

定义(集上的二元运算)：
设S为非空集合，那么S×S到S的映射称为S的结合法或运算。
$\left\{ \begin{aligned} S×S & → S \\ (a, b) & → ab \\ \end{aligned} \right.$
称为集合S上的二元运算。S叫做代数系。

代数结构(R, *)，二元运算根据封闭性、单位元、逆元、结合律、交换律，可以归纳成不同的群。从最不严格到严格(依次添加限制条件)，其关系图如下：
在这里插入图片描述
原群
原群(magma)是一种基本的代数结构，只要满足两元素作二元运算得到新元素仍属于该集合，即封闭性。维基百科原文如下：

A magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation $\times M \rightarrow M$ . The binary operation must be closed by definition but no other properties are imposed.

半群
半群(Semigroup)，满足结合律(associative property)的代数结构。V=<S，* >，其中二元运算是可结合的，即(ab)c=a(b*c)，则称V是半群。维基百科原文如下：

A semigroup is an algebraic structure consisting of a set together with an associative binary operation.

幺半群
幺半群(monoid)在半群的基础上，还需要满足有一个单位元。维基百科原文如下：

A monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are semigroups with identity.

一、群（Groups）

1. 基本定义

定义群(group)是两个元素作二元运算得到的一个新元素，需要满足群公理(group axioms)，即：
设群G是一个具有结合法的非空集合，其中 ◦ 是该集合的二元运算。

封闭性(Closure)：For all g, h ∈ G, g ◦ h ∈ G.
结合律(Associativity)：For all g1, g2, g3 ∈ G, (g1 ◦ g2) ◦ g3 = g1 ◦ (g2 ◦ g3).
单位元 (Existence of an identity)：There exists an identity e ∈ G such that for all g ∈ G, e ◦ g = g = g ◦ e.
逆元(Existence of inverses)：For all g ∈ G there exists an element h ∈ G such that g ◦ h = e = h ◦ g. Such an h is called an inverse of g.

A group is a set of elements together with an operation that combines any two of its elements to form a third element satisfying four conditions called the group axioms, namely closure, associativity, identity and invertibility.

当 G 的结合法 ◦ 写作加法时，这个e叫做G中的零元，通常记作0。
当 G 的结合法 ◦ 写作加法时，逆元通常叫做负元，记作-a。

如整数集合，二次元运算为加法就是一个群(封闭性是显然的，加法满足结合律，单位元为0，逆元取相反数-a)。

如果群的二元运算 ◦ 满足交换律，那么G叫做阿贝尔群(abelian)：

交换律(Commutativity)：For all g, h ∈ G, g ◦ h = h ◦ g.

An abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order (the axiom of commutativity).

定义群G的元素个数叫做群G的阶，记为|G|。当|G|为有限数时，G叫做有限群，否则G叫做无限群。
定义设a为群G中的元素，则称使得aⁿ=e的最小正整数n为元素a的阶，记为|a|，如果这样的n不存在，则称a的阶为无限（或称是零）。
性质 1.1.1 设S是个具有结合法的非空集合，则S中的单位元e是惟一的。
性质 1.1.2 设S是个有单位元的半群，则对S中的可逆元a，它的逆元a’是惟一的。
性质 1.1.3 设a₁,…,a_n是群G中n≥2个元素，则对1≤i₁＜…<i_k<n，有 $a_{1}...a_{i_{1}})...(a_{i_{k}}...a_{n})=a_{1}a_{2}...a_{n-1}a_{n}$ 此性质说明，在有结合律的情况下，可有序结合一些元素作乘积，但最终的乘积结果是确定的。
性质 1.1.4 设a₁,…,a_n是群G中n≥2个元素，则 $a_{1}a_{2}...a_{n-1}a_{n})^{-1}=a_{n}^{-1}a_{n-1}^{-1}...a_{2}^{-1}a_{1}^{-1}$ 性质 1.1.5 设a₁,…,a_n是群G中n≥2个元素，则对1, 2, …, n的任意排列i₁，i₂，…，i_k，有 $a_{i_{1}}a_{i_{2}}...a_{i_{n}}=a_{1}a_{2}...a_{n-1}a_{n}$ 性质 1.1.6 设a是群G 中的任意元，则对任意的整数m,n，有 $a^ma^n=a^{m+n}, (a^m)^n=a^{mn}$

2. 子群

如果群G的子集H对于群G的运算也构成了群，则称H为群G的子群，记作H ≤ G。H={e}和H=G都是群G的子群，叫做群G的平凡子群(trivial subgroup)，否则叫做G 的真子群(strict subgroup)。

群G的子集H称为子群，若
1）1∈H；
2）若x,y∈H，则xy∈H，即H在运算下封闭；
3）x∈H，则x^-1∈H。

定理 1.2.1 设H是群G的椅子非空子集合，则H是G 的子群的充要条件是：对任意a, b∈H，有ab^-1∈H。
定理 1.2.2 群G的任意一簇子群的交集还是G的子群。多个子群的并集不一定是子群。
定义如果群G中存在一个子集H，使得子集H中的任意元素b，都可以表示为H中某个特殊的元素a的幂次，则称子集H为群G的循环子群，而称元素a为H的生成元，记为H=(a)。特别地，若H=G，则称群G为循环群。
在这里插入图片描述

3. 正规子群和商群

集合的积：设X和Y是群G的两个非空子集，于是子集X与Y 的积记为 $XY=\{xy|x∈X, y∈Y\}$ 特别地，如果Y={y}是一个单元素集，而子集X={x₁, x₂, …}，那么子集X和Y的积为
$XY=\{x_{1}y, x_{2}y, …\}$ 此时我们记XY为Xy，并称Xy为元素y右乘X的积。

定义设H为群G的子群，a∈G，则称群G的子集 $aH=\{ax|x∈H\}$ 为群G关于子群H的一个左陪集，而称 $Ha=\{xa|x∈H\}$ 为群G关于子群H的一个右陪集。同时称a为代表元。如果aH=Ha，则aH叫做G中H的陪集。

定理 1.3.1 设H为群G的子群，则任意a，b∈G，Ha=Hb。与下面两个条件等价
1）a∈Hb
2）ab^-1∈H

定理 1.3.2 设H为群G的子群，则任意a，b∈G，aH=bH。与下面两个条件等价
1）a∈bH
2）b^-1a∈H

定理 1.3.3 设H为群G的子群，则任意a∈G，有aH=a=Ha。

推论设H为群G的子群，则G可以表示为不相交的左（右）陪集的并集。
类似于完全剩余系组成新集合，左陪集全体也可组成新集合。

定理 1.3.4 设H为群G的子群，a，b∈G，则
1）a∈Ha
每个右陪集的代表元都含在该右陪集内，一个群元素只能属于一个陪集

2）右陪集Ha与Hb或者相等或者相交为空集，即 Ha=Hb 或 Ha∩Hb=Φ
任两个右（左）陪集要么相等，要么不相交

3）G=∪_a∈GHa
群G的所有不重复的右陪集构成了G的一个划分，陪集为群G元素的一种划分，每个元素属于且只属于一个类(陪集)

定义设H为群G的子群，由上述定理决定的G的划分 $G=∪_{a∈G}~Ha$ 称为G的一个右陪集分解。

特别地，由上可见群G的右陪集分解具有如下特点：
1）分解式中必含有子群H（即以单位元为代表的右陪集），而其余的右陪集都不是G的子群；
2）右陪集分解式中出现的右陪集彼此都不相交；
3）分解式中每个右陪集的代表元都可以适当替换。

定义设H为群G的子群，若记
S_R={Ha|a∈G}, SR为H的所有不重复的右陪集组成的集合，
S_L={cH|c∈G}，SL为H的全部不重复的左陪集组成的集合。
则左陪集将与右陪集具有完全相似的性质。同时有如下结论：

定理 1.3.5 设H为群G的子群，则S_R与S_L之间存在双射。即S_R与S_L中的元素个数相同。

定义设H为群G的子群，则H在G中不同左（右）陪集组成的新集合 ${aH | a ∈ G\}（对应地 \{Ha | a ∈ G\}）$ 叫做H在G中的商集，记作G/H。 $G/H=\{aH | a ∈ G\}=\{a_{i}H | i ∈ I\}$ G/H中不同右（左）陪集的个数为H在G中的指数（指标），记为[G:H]。

引理 1.3.1 设H为群G的子群，则H与H的任一个右陪集Ha之间都存在双射。
由引理1.3.1可知，子群的互不相等的右陪集不相交且彼此都含有相同数目的元素。

定理 1.3.6 设H为群G的子群，则 $∣ G ∣ = [G : H] ∣ H ∣$ 更进一步地，如果K，H是群G的子群，且K是H的子群，则 $[G : K] = [G : H] [H : K]$ 如果其中两个指标是有限的，则第三个指标也是有限的。

推论(Lagrange) 设H为群G的子群，若 |G|=N，|H|=n 且 [G:H]=j，则 N=nj 。即子群H的阶是|G|的因数。

推论设G为有限群，则任意a∈G，其阶m必是|G|的因子，即|a|||G|。

最后，讨论商集G/H构成一个群的条件（H为正规子群）。
定理 1.3.7 设N是群G的子群，则以下条件是等价的：
（i）对任意a∈G，有aN=Na。
（ii）对任意a∈G，有aNa^-1=N。
（iii）对任意a∈G，有aNa^-1 ⊆ N，其中aNa^-1={ana^-1 | n∈N }。

定义设N是群G的子群，称N是G的正规子群，如果它满足上述条件。

定理 1.3.8 设N是群G的正规子群，G/N是由N在G中的所有（左）陪集组成的集合，则对于结合法 $(a N) (b N) = (a b) N$ G/N构成一个群。

4. 循环群

首先讨论加群Z及其子群。
定理 1.4.1 加群Z的每个子群H都是循环群，并且有H=<0>或H==mZ，其中m是H中最小的正整数。如果H≠<0>，则H是无限的。

定理 1.4.2 每个无限循环群同构于加群Z。每个阶为m的有限循环群同构于加群Z/mZ。

定义设G是一个群，a∈G，则子群< a >的阶称为元素的阶，记为ord(a)。

定理 1.4.3 设G是一个群，a∈G，则
（i）a^k=e 当且仅当k=0.
（ii）元素a^k（k∈Z）两两不同。
当a的是有限阶m>0，有
（iii）m是使得a^m=e的最小正整数
（iv）a^k=e 当且仅当m|k
（v）a^r=a^k当且仅当r＝k（mod m）
（vi）元素a^k（k∈Z/mZ）两两不同。
（vii）< a >={a⁰, …, a^m-1}
（viii）对任意整数1≤d≤m，有ord(a^d)=m/(d, m).

定理 1.4.4 循环群的子群也是循环群。

定理 1.4.5 设G是循环群。
（i）如果G是无限的，则G的生成元为a和a^-1.
（ii）如果G是有限阶m的，则a^k是G的生成元为当且仅当(k, m)=1.

二、环（Ring）

1. 环的定义

环在交换群基础上，进一步限制条件。环、交换环、域间的关系如下：
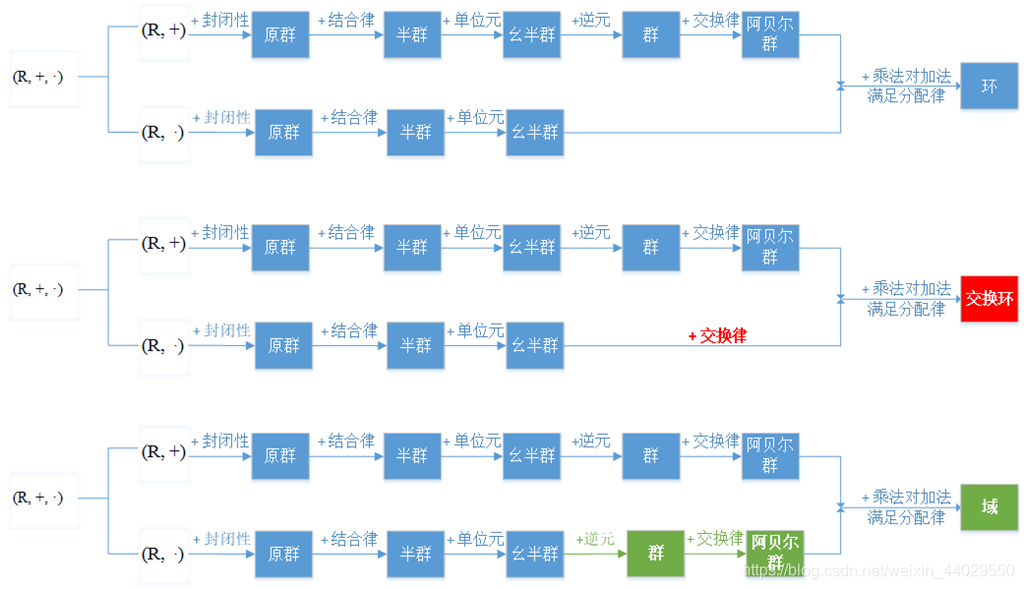
在这里插入图片描述
维基百科有一张表从不同角度呈现这三者的关系，如下：

定义环(ring)在阿贝尔群(也叫交换群)的基础上，添加一种二元运算·(虽叫乘法，但不同于初等代数的乘法)。设R是具有两种结合法（通常是加法和乘法）的非空集合，需要满足环公理(ring axioms)。环公理如下：
(1) (R, +)是交换群
封闭性：a + b is another element in the set
结合律：(a + b) + c = a + (b + c)
单位元：加法的单位元为0，a + 0 = a and 0 + a = a
逆元：加法的逆元为-a，a + (−a) = (−a) + a = 0 (对于所有元素)
交换律：a + b = b + a
(2) (R, ·)是幺半群
结合律：(a ⋅ b) ⋅ c = a ⋅ (b ⋅ c)
单位元：乘法的单位元为1，a ⋅ 1 = a and 1 ⋅ a = a
(3) 乘法对加法满足分配律 Multiplication distributes over addition
a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c) for all a, b, c in R (left distributivity)
(b + c) ⋅ a = (b ⋅ a) + (c ⋅ a) for all a, b, c in R (right distributivity)
如果还满足
(4) 二元运算乘法还满足交换律
对任意的a，b∈R，有ab=ba，则R为交换环（commutative ring）。
(5) 对任意a∈R，有a1_R=1_Ra=a，则R叫有单位元环。

A ring is an abelian group with a second binary operation (The abelian group operation is called “addition” and the second binary operation is called “multiplication” in analogy with the integers) that is distributive over addition and is associative.
One familiar example of a ring is the set of integers. The integers are a commutative ring, since a times b is equal to b times a. The set of polynomials also forms a commutative ring. An example of a non-commutative ring is the ring of square matrices of the same size.

定义若环R中存在非零元素a和b，使得
$a \cdot b = 0$ 则称a是R的一个左零因子，b是R的一个右零因子，进一步地，若环R中的元素a既是左零因子，又是右零因子，则称a为零因子。
注：此处等式右边的0指的是加法的零元。

定义若环R中没有左零因子（自然也就没有右零因子），则称环R为无零因子环。

定义
1）若环{R,+,·}中具有乘法运算的单位元，则称环{R,+,·}为有单位元环。
2）若环{R,+,·}中的乘法运算满足交换律，则称环R为可换环/交换环（交换环需不需要含单位元目前有争议）。
3）一个不含零因子的交换环称为整环(Integral Domain)。
4）若环{R,+,·}中的非零元在乘法运算下构成群，则称环{R,+,·}为除环。
5）可交换的除环称为域。

性质 2.1.1 设R是整环，则R中有乘法消去律成立：当ca=cb，c≠0时，a=b。

定理 2.1.1 每个域都是整环。

注意：
1）环中的乘法单位元显然不只代表整数1，例如{Z7,+, ·}中的单位元为[1]。
2）并不是每个环都有单位元，例如偶数环。
3）若环R中有单位元,则这个单位元必是唯一的。

定义若环R的一个子集S在环R的加法和乘法运算下也构成环，则称S为R的子环。

定义若整环（除环或域）R的子集S在整环（除环或子域）R的加法和乘法运算下也构成整环（除环或域），则称S为整环（除环或域）R的子整环（子除环或子域）。

定义设I是环R的一个子环，若任意a∈I，任意r∈R，都有ra∈I（或ar∈I），则称I是R的一个左理想（或右理想）；若任意a∈I，任意r∈R，都有ar∈I且ra∈I，则称I是R的一个理想（理想子环的简称）。

注：
由理想的定义可知，理想的乘法具有“吸收性”。
任一个环R至少都有如下两个理想：{0}—零理想，R—单位理想，统称为环R的平凡理想，而将其它理想（若存在）称之为环R的真理想。

2. 域的定义

域(Field)是定义了两个二元运算：加法和乘法的非空集合。
1）该集合对加法构成了阿贝尔群，其加法的零元记为0；
2）集合中的所有非零元对乘法也构成了阿贝尔群，其乘法的单位元记为e，且0≠e。
3）两个二元运算乘法和加法通过分配律a(b+c)=ab+ac联系在一起。
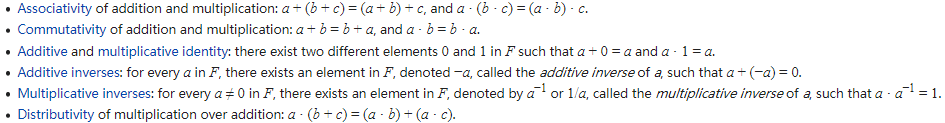
在这里插入图片描述

A field is a nonzero commutative ring that contains a multiplicative inverse for every nonzero element, or equivalently a ring whose nonzero elements form an abelian group under multiplication.
As such it is an algebraic structure with notions of addition,subtraction, multiplication, and division satisfying the appropriate abelian group equations and distributive law.

定义只包含有限个元素的域称为有限域，或迦罗瓦（Galois）域。

从有限域到交换环一些代数结构的从属关系如下：

rngs ⊃ rings ⊃ commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ GCD domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ algebraically closed fields

在这里插入图片描述

3. 多项式环

设R是任意环，则环R上的多项式可以表示为 $f(x)=a_{0}+a_{1}x+…+a_{n}x^n$ 其中n为非负整数，系数a_i为环R上的元素，x是不属于环R的一个符号，称为环R上的不定元（或称未定元）。
约定当系数a_i=0时，项a_ixⁱ可以不写，在此约定下，上面的多项式也可以等价地表述为 $f(x)=a_{0}+a_{1}x+…+a_{n}x^n+0x^{n+1}+...+0x^{n+h}$ 其中h为任意正整数。
这样，对环R上的两个多项式
$f(x)=a_{0}+a_{1}x+…+a_{n}x^n\\ g(x)=b_{0}+b_{1}x+…+b_{m}x^m$ 进行比较时，就可以假设他们都具有相同的幂指数。

环R上的两个多项式相等的充要条件可以表示为： $\leftrightarrow a_{i}=b_{i}，0≤i≤n$

两个多项式f(x)与g(x)的加法与乘法运算分别定义为
$f(x)+g(x)=(a_{0}+b_{0})+(a_{1}+b_{1})x+…+(a_{n}+b_{n})x^n\\ f(x)g(x)=c_{0}+c_{1}x+… +c_{n+m}x^{n+m}$ 其中， $c_{k}=\sum_{i+j=k,0≤i≤n,0≤j≤m}a_{i}b_{j}$

容易验证环R上的多项式集在定义了如上的多项式的和与乘积运算之后构成环。称之为环R上的多项式环，记为R[x]。

R[x]中的零元是系数全为零的多项式，这个多项式称为零多项式，记为0。

定义设 $f(x)=a_{0}+a_{1}x+…+a_{n}x^n$ 为环R上的一个非零多项式，故可设a_n≠0，并称a_n为多项式f(x)的首系数，a₀为f(x)的常数项，而n称为f(x)的次数，记
$n = d e g (f (x)) = d e g (f)$ 并约定 $d e g (0) = - \infty$ 次数≤0的多项式称为常数多项式。若环R有单位元1且f(x)的首系数为1，就称f(x)为首一多项式。

多项式的分类和性质：
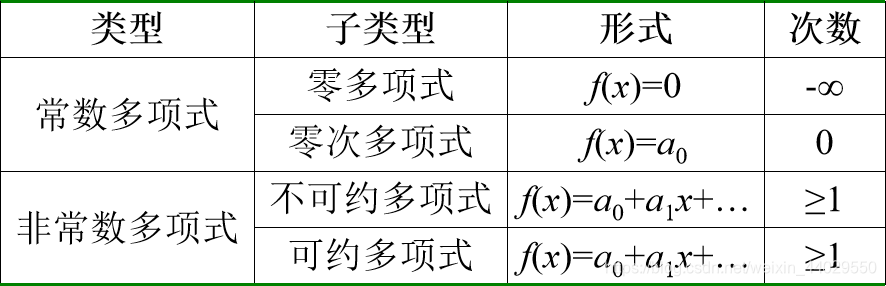
在这里插入图片描述
定理 2.3.1 设f(x)和g(x)∈R[x]，则
$deg(g(x)))\\ deg(f(x)·g(x))≤deg(f(x))+deg(g(x))$ 若R是整环，则
$d e g (f (x) \cdot g (x)) = d e g (f (x)) + d e g (g (x))$
定理 2.3.2 设R是一个环，则R[x]是可换环当且仅当R是可换环；R[x]是有单位元的环当且仅当R有单位元；R[x]是整环当且仅当R是整环。
并且与整数环上的素数相对应，在域F上的多项式环F[x]上可以定义既约多项式（或称为不可约多项式）。

定义（不可约多项式） ：设f(x)是次数大于零的多项式，若除了常数和常数与多项式f(x)本身的乘积以外，f(x)再不能被域F上的其它多项式除尽，则称f(x)为域F上的既约多项式或不可约多项式。否则，f(x)为合式。

（补充）：设F是域，则非常数多项式f(x)∈F[x]在F[x]中是不可约的当且仅当在F[x]中没有如下的因子分解： $f (x) = g (x) h (x)$ 其中deg(g), deg(h) < deg(f)。
注：
以上定理说明deg(g), deg(h) >0，即g(x)和h(x)不能为常数多项式，否则条件deg(g), deg(h) < deg(f)得不到满足。

注：由此定义我们可以看出：
1） f(x)是不可约多项式的充要条件为f(x)不能再分解为两个次数比f(x)的次数更低的多项式的乘积。
2） f(x)是否可约与所讨论的域有很大关系。例如
$f(x)=x^2+1$
在实数域上是不可约的，但在复数域上可分解为
$f (x) = (x + i) (x - i)$ 但不论在哪一个域上，凡是一次首一多项式都是不可约多项式。

定理 2.3.3 设f(x)和g(x)∈F[x]，g(x)≠0，则存在多项式q(x)和r(x)∈F[x]，使得 $f (x) = q (x) g (x) + r (x)$ 其中 $d e g (r (x)) < d e g (g (x))$ 注：在整环和域中，这种分解形式是唯一的。

定理 2.3.4 域F的多项式环F[x]中的每一个首一多项式必定可以分解为首一不可约多项式的乘积，并且当不考虑因式的顺序时，这种分解是唯一的。

4. 整环中的因子分解

在数论中我们讨论了整数环的唯一分解定理，在前一节中我们又看到这样这个定理对于多项式也是成立的，而他们的共性在于它们都是有单位元的整环，为此本节讨论有单位元的整环中元素的分解问题。

定义设D是有单位元的整环，则任意a, b∈D，
1）若c=ab，则称a是c的因子，并称a可整除c，记作a|c。
2）若a|b且b|a，则称a与b相伴，记作a~b。
3）若a与b之积ab为单位元，则称a与b互为逆元，此时也称a与b皆为可逆元（或称a与b为单位）。
4）若c=ab，且a与b都不是可逆元，则称a是c的真因子。

由以上定义可得以下基本事实，其中集合U(D)表示整环D中的所有可逆元构成的集合（因其是乘法群，故也称作单位群）：
1）由于任意a∈D，均有0=a·0，a=a·1，因而任意元素都是0的因子，而单位元l是任意元素的因子。
2）由于若u∈U(D)，则任意a∈D，均有a=u(u^-1a)，因而可逆元是任意元素的因子。
3）由于任意a, b, c∈D，若a|b且b|c，则a|c，因而整除关系满足传递性。
4）两元素相伴，则它们相差一个可逆元因子：设a~b，则a|b且b|a，即存在元素u和v使得 $b = u a ， a = v b$ 因而b=uvb，由于D中有单位元且无零因子，因而由b(1-uv)=0，即得uv=1，所以u和v都是可逆元。
5）相伴关系是等价关系。
6）可逆元无真因子，且所有可逆元都与单位元l相伴.

定义设D是有单位元的整环，且D*为D中的所有非零元构成的集合，则任意a, b∈D，p∈D*\U(D)，
若由等式p=ab，可知a∈U(D)，或b∈U(D)，则称p是不可约元或既约元；
若由p|ab，可知p|a或p|b，则称p是素元。

注：
1）“\”表示集合的减法运算；
2）由以上定义可知，既约元或者素元一定不是可逆元；
3）既约元没有真因子。
在整数环中，既约元与素元均是指全体素数；但在高斯整数环中，素数就不一定是既约元了。

对于一般的有单位元的交换环，既约元与素元往往是两个不同的概念。但是如果在有单位元的整环中，既约元与素元的关系有以下定理：
定理 2.4.1 设D是有单位元的整环，则D中的素元必是既约元。

为了给出定理2.4.1的逆定理成立的条件（即既约元是素元的条件），我们需要引出如下定义：
定义设D是有单位元的整环，任意a, b∈D，若存在d∈D使得以下两个条件成立，则称d是a和b的最大公因子。
1）d|a，d|b；
2）任意d’∈D，若d’|a且d’|b，则d’|d。

注：
最大公因子跟我们在数论部分所说的最大公因数类似，但是有区别。

由以上定义可以得到最大公因子的以下简单性质：
引理 2.4.1 a与b的任意两个最大公因子是相伴的。

注：
上述引理表明最大公因子不唯一，因而以下当a与b的最大公因子存在时，以(a,b)表示a与b的任意一个最大公因子。

引理 2.4.2 (a,(b,c))~((a,b),c)。
引理 2.4.3 c(a,b)~(ca, cb)=(ac, bc)。
引理 2.4.4 若(a,b)~1，(a,c)~1，则(a,bc)~1。

定理 2.4.2 设D是有单位元的整环，若任意a, b∈D，(a, b)存在，则D中的每个既约元也是素元。

定义（唯一分解整环）
设D是有单位元的整环，若任意a∈D*\U(D)
1）a可分解为有限个既约元之积，即a=p₁p₂…p_s，其中pi，i=1, 2, …, s，为既约元。

2）若a=p₁p₂…p_s=q₁q₂…q_t，其中p_i，1≤i≤s，q_j，1≤j≤t，均为既约元，则s=t，且适当调换次序后可以使得p_i ~ q_i（1≤i≤s），则称D是p₁p₂…p_s(Unique Factorization Domain, UFD)。

由以上定理知唯一分解整环有以下重要性质：
定理 2.4.3 设D是唯一分解整环，则D中任何两个不全为0的元素均有最大公因子，因而D中每一个既约元也是素元。

定理 2.4.4 设D是有单位元的整环，则以下三个命题等价：
1）D是唯一分解整环。
2）D满足下列两条件：
a）D中的任意真因子序列a₁, a₂, …, a_i, … (其中a_i+1是a_i的真因子)只能含有有限项。
b）D中任何两元素均有最大公因子。
3）D满足下列两条件：
a）D中的任意真因子序列a₁, a₂, …, a_i, … (其中a_i+1是a_i的真因子)只能含有有限项。
b）D中每一既约元都是素元。

引理 2.4.5 在唯一分解整环内，n次代数方程最多有n个根。

定理 2.4.5 域的乘群的任何有限子群是循环群。

主理想整环 （Principal Ideal Domain, PID）
如果理想中的一切元素都是由一个元素的倍数及其线性组合生成，则称这个理想为主理想，具体定义如下：

定义在可换环R中，由一个元素a∈R所生成的理想
$I(a)=\{ra+na|r∈R, n∈Z\}$ 称为环R的一个主理想，称元素a为该主理想的生成元。

注：
运算ra表示环中的乘法运算，na表示加法的幂次运算。

如果在一个有单位元的整环中每一个理想都是主理想，则此环称为主理想整环。

定理 2.4.6 每个主理想整环都是唯一分解整环。
推论设D是主理想整环，a，b∈D，d是a，b的最大公因子，则存在p, q∈D，使
$p a + q b = d$
推论设D是主理想整环，p是既约元，则D/(p)是域。

欧几里得整环 （Euclidean domain）
定义设D是有单位元的整环，若存在一个从D的所有非零元构成的集合D到非负整数集的映射d，使得取定a∈D之后，任意b∈D，都存在q，r∈D，使得
$b = q \cdot a + r$ 这里r=0 或者d(r)<d(a)，则称D为欧几里得整环 (简称欧氏环)。

注：
大家可以把映射d想象成多项式的次数deg。
实际上我们看到欧式环就是能进行某种意义下的带余除法的环。

定理 2.4.7 欧氏环是主理想整环，因而是唯一分解整环。

5. 由整环构造域

只要给定欧氏环D以及素元p，就可以构造一个域。

定理 2.5.1 若D是欧式环，p是素元，则D_p构成域。

1）给定欧式环D及其一个素元p，构造域的过程
在这里插入图片描述
2）由多项式环D=F_p[x]构造有限域的过程，其中x的系数取自域F_p=Z (mod p)，p为素元。

参考资料：
信息安全数学基础（清华大学出版社）
维基百科
Spark & Shine

群、环、域知识点整理（持续补充ing）

目录

前言