蒙特卡洛方法入门 笔记

简介

原理:按照问题情景下的采样方式，通过大量的随机样本，对系统进行模拟，从而求得所需计算的参量。

可以认为，蒙特卡洛方法粗略分为2类。第一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程。这一类下，核物理研究中，分析中子在反应堆中的传输过程是一个较为典型的例子。第二类则是所求解问题可以转化为某种随机分布的特征数，比如通过投点法近似估算圆周率、近似计算定积分、随机事件出现的概率，或者随机变量的期望值。

本篇文章侧重讲解第二类情况。

蒙特卡洛近似求圆周率（投点法）

import random

def monte_carlo():
    n = 1000000
    r = 1.0
    a, b = (0.0, 0.0)
    x_neg, x_pos = a - r, a + r
    y_neg, y_pos = b - r, b + r

    count = 0
    for i in range(0, n):
        x = random.uniform(x_neg, x_pos)
        y = random.uniform(y_neg, y_pos)
        if x*x + y*y <= 1.0:
            count += 1

    print (count / float(n)) * 4

蒙特卡洛求定积分

最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。

先从概率分布为均匀分布的简单例子入手：

假定自变量x在[a,b]之间均匀分布，对于


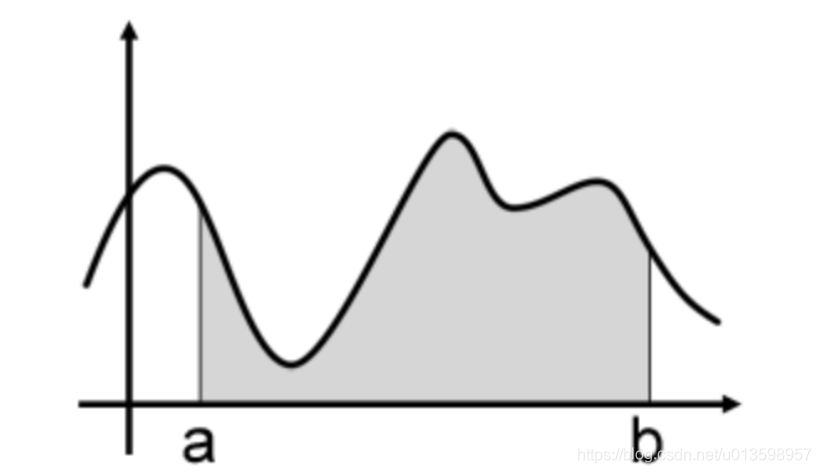
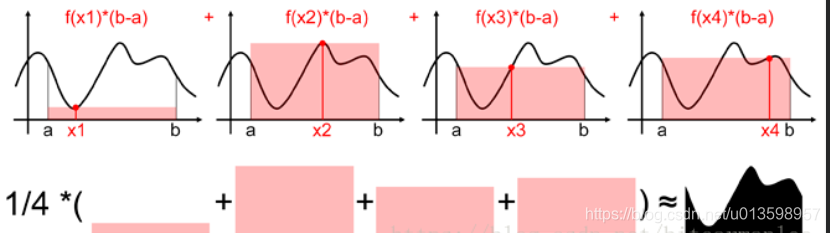
用采样（采样的进行，后面会提到）的一个值代表[a,b]区间上所有的f(x)的值，解法过于粗糙。那么可以采样[a,b]区间的n个值：x0,x1,…xn−1,用它们的均值来代表[a,b]区间上所有的f(x)的值，即：

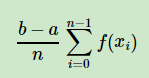
但多数情况下，概率分布不是均匀分布的。

如果知道x在[a,b]区间的概率分布函数p(x)，求和可以这样进行：

这个形式就是蒙特卡罗方法的一般形式。（连续函数形式，但是在离散时一样成立）。

代入均匀分布的条件，即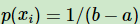，不难发现均匀分布也可以作为p(x)的特例。

关于采样的简单记录

得到了x的概率分布函数p(x），便可以基于它去采样同样服从这个分布的含n个x的样本集。如何进行采样呢？

对于常见的均匀分布uniform(0,1)，采样样本很容易。其实，其他常见的概率分布，无论是离散的分布还是连续的分布，它们的样本都可以通过uniform(0,1)的样本转换而得。

对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到，或者说接近该分布的样本。 如果p(x)十分复杂，那么可以设定一个程序可采样的常见分布 q(x)， 比如高斯分布，然后按照一定的方法拒绝某些样本。

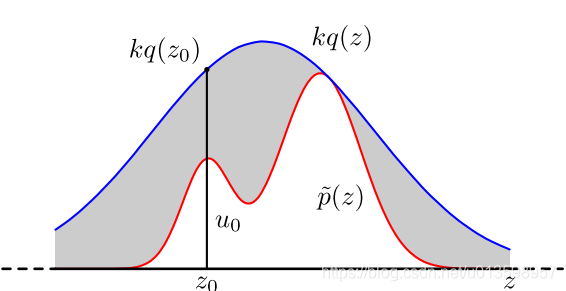
上图的例子中，首先设定一个高斯分布q(x)和常数k，使得 p(x) 总在 kq(x) 的下方。

接下来，对方便采样的q(x)，按前面提到方法进行采样。然后，从均匀分布（0,kq(z0))中采样得到一个值u。如果未落在实际分布的区域中，则拒绝这次抽样。重复以上过程得到n个接受的样本：z0,z1,…zn−1,最终有

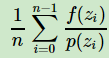
可见，设定一个易采样的分布 ，然后按照一定的方法拒绝某些样本，以达到接近 实际概率分布p(x)分布的目的。

但是，接受-拒绝采样也只能部分满足我们的需求，在很多时候还是很难得到概率分布的样本集，如一些稍特别的二维分布和高维非常见分布。