【线性代数的本质】— 个人笔记
最近了解到B站up主搬运和配音的一个对线性代数的大概认知的视频,里面重点关注把原本我认为“枯燥”的知识用几何图像来讲解,生动地阐述了“线性变换”这一词。
除了丰富生动的几何图像,作者讲解后面部分的新知识时,总是提到前面相对基础的知识,提示我们知识之间的联系以及基、数乘、矩阵乘法这些基础的关键。其中一个理解起来较有难度的联系例子便是对偶性,不得不说这才是系统化的学习。
当然,真正的学习、理解和掌握需通过解决问题来实现。本讲解关注的是直观、理解角度,有助于我们更好地认识线性代数。(直观思维也是很好的学习方法)
分享链接:-UP主汉语配音-【线性代数的本质】合集-转载于3Blue1Brown官方双语】
00 序言
对线性代数的理解可以分为数值水平和几何水平,提高前者有利于顺利使用,提高后者更有利于你清楚理解为什么和怎么使用。培养几何直觉十分关键。
线性代数中计算和可视化理解之间的联系往往相当直观。
01 向量
什么是向量:有向箭头(物理)、有序数字列表(建模)(计算机)、前两者联系概括,放入坐标(数学家)。
向量加法的过程几乎是线性代数中唯一允许向量离开原点,可以理解为向空间中跨出一段距离。
数乘:缩放
线性代数围绕向量加法和向量数乘两种基本运算进行,来操纵空间。
02 张成的空间与基
如二维平面有基向量i 和 j,基向量实际就是标量对象。

可以选择不同的基向量,构建不同的坐标系。

当然,也有共线,甚至都为零向量的情况。
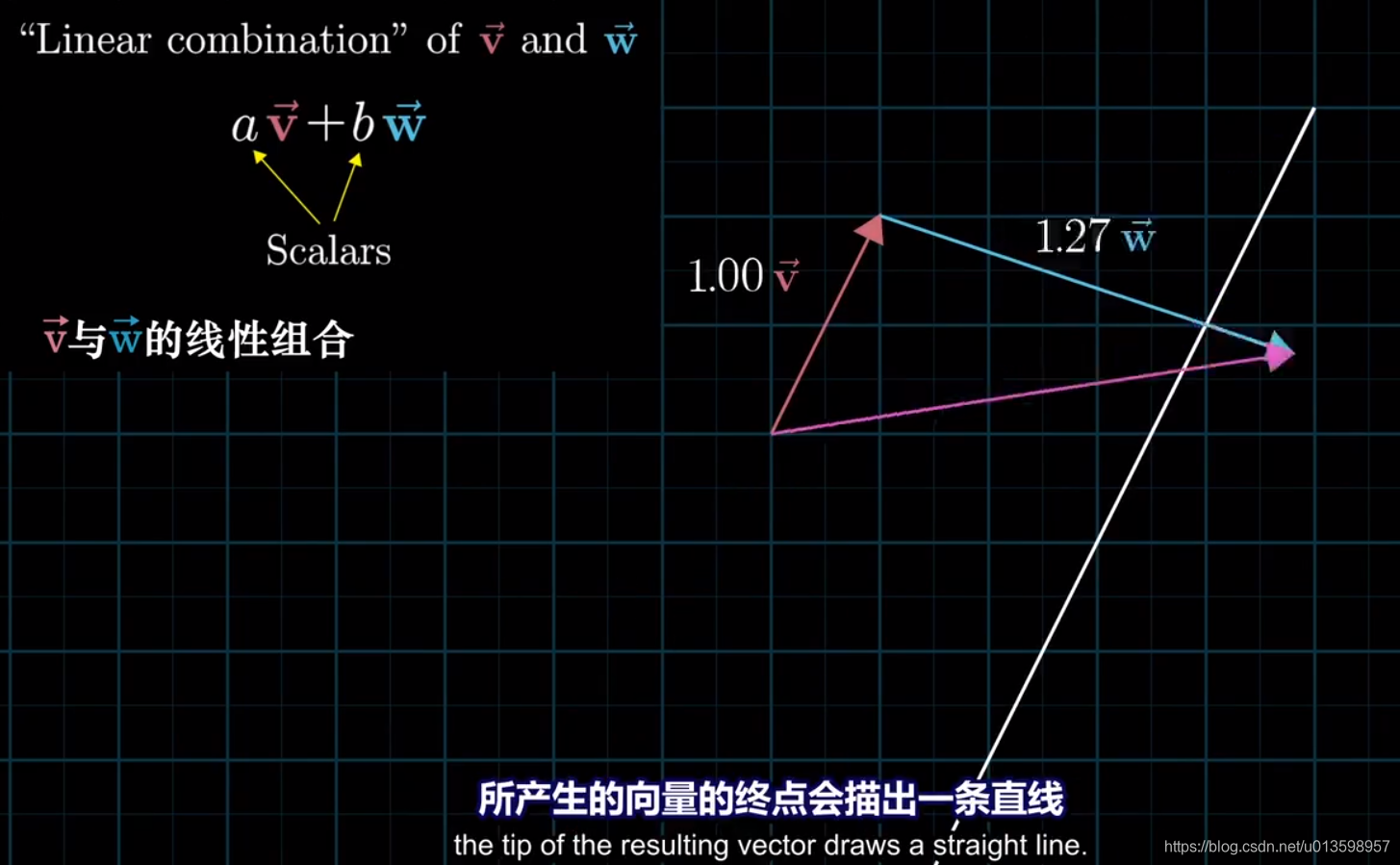
所有可以表示为给定向量 组合 的 向量的集合 被称作给定向量张成的空间。(仅通过上述提到的两种运算)
可以将每个向量抽象为点来理解空间。
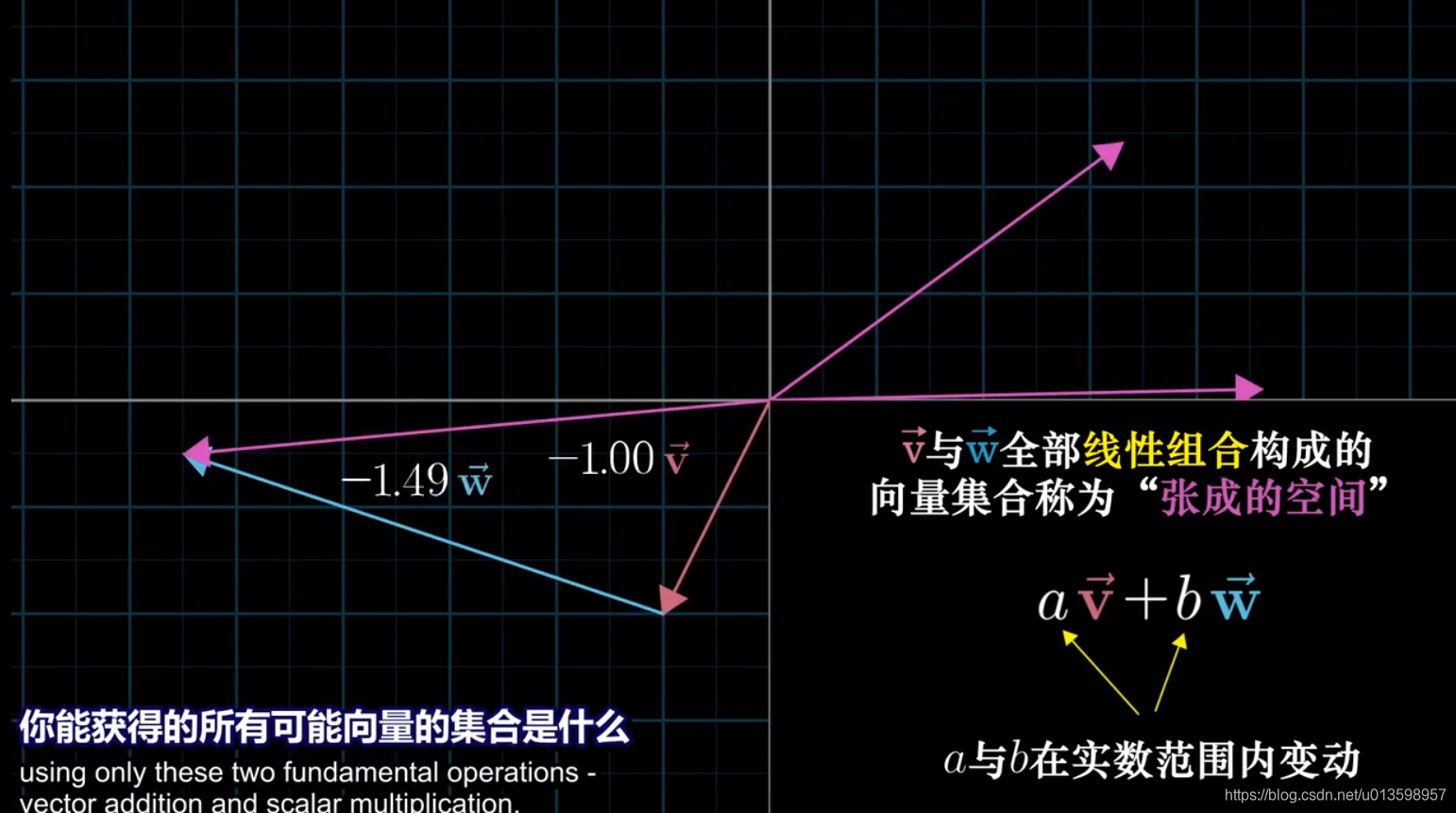
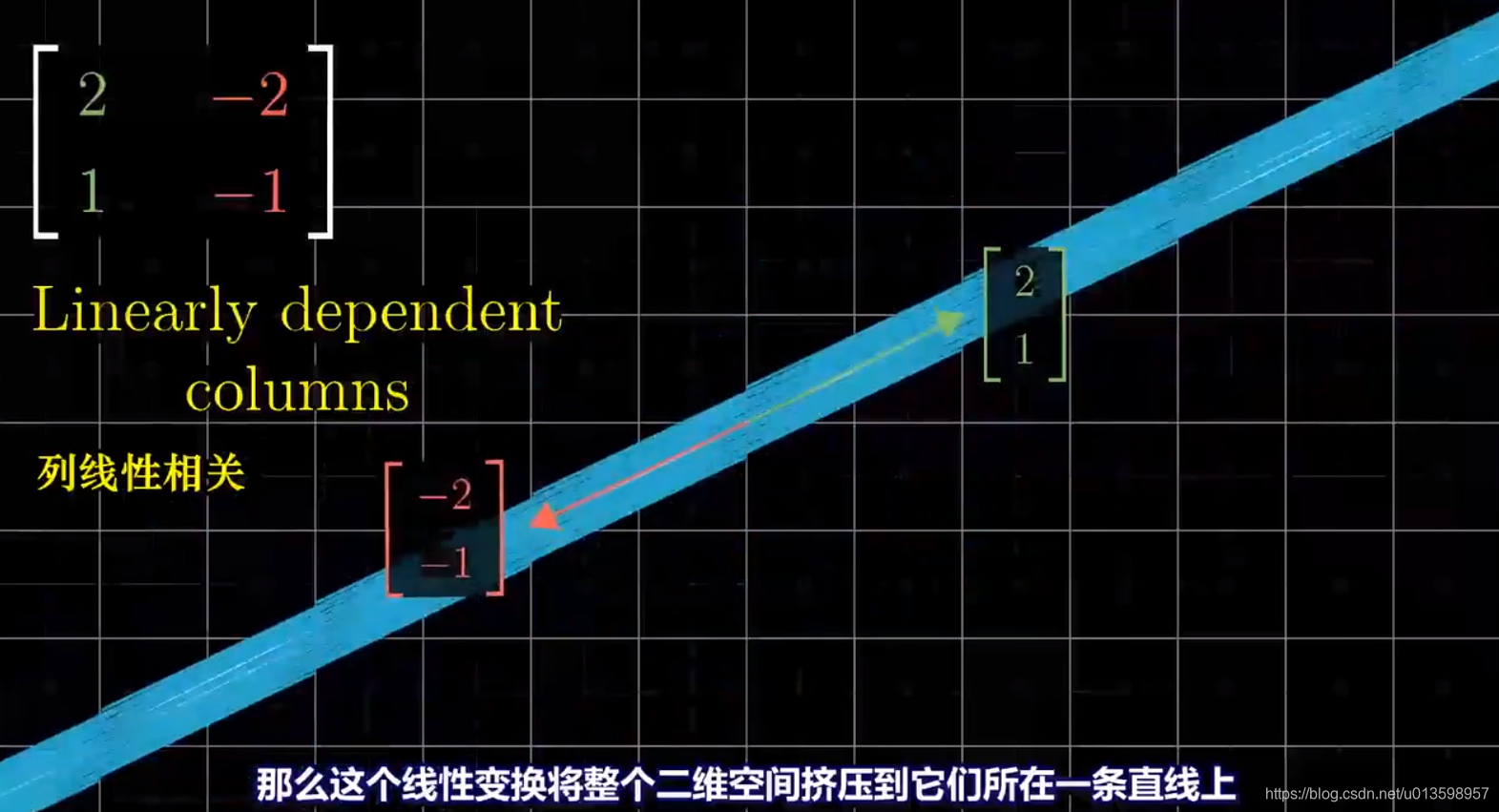
线性相关(落在已张成的空间,对空间无拓展奉献,“多余”):其中一个向量可以表示为其他向量的线性组合。
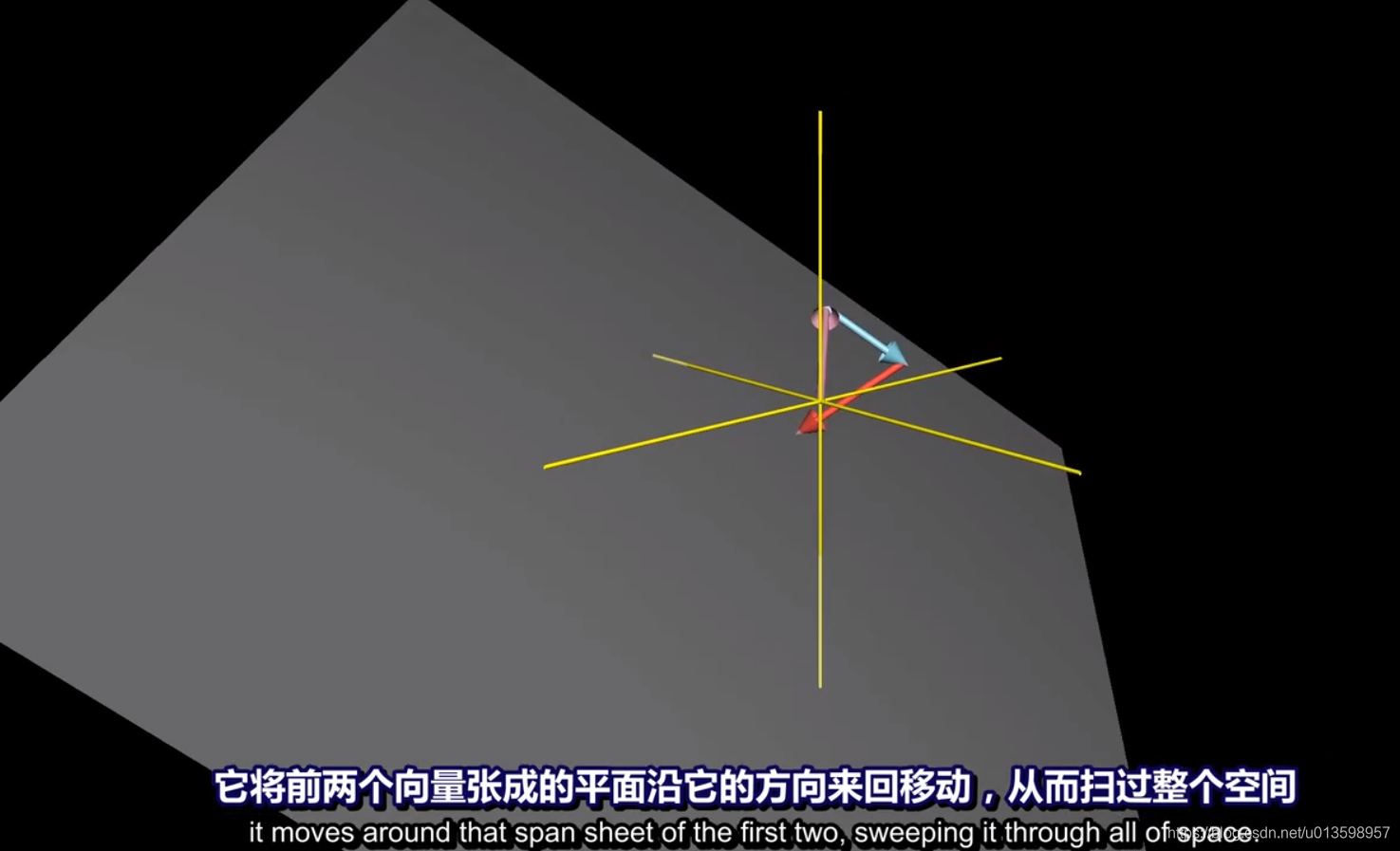
线性无关:所有向量为张成的空间增添新的维度。
向量空间的一组基是张成该空间的一个线性无关的向量集。
03 矩阵与线性变换
变换可以看作是可视化运动的函数。

线性变换:1.直线在变换后保持为直线,不能有所弯曲;2.原点必须保持固定。

借助基向量的变换,即可理解整个空间的线性变换:
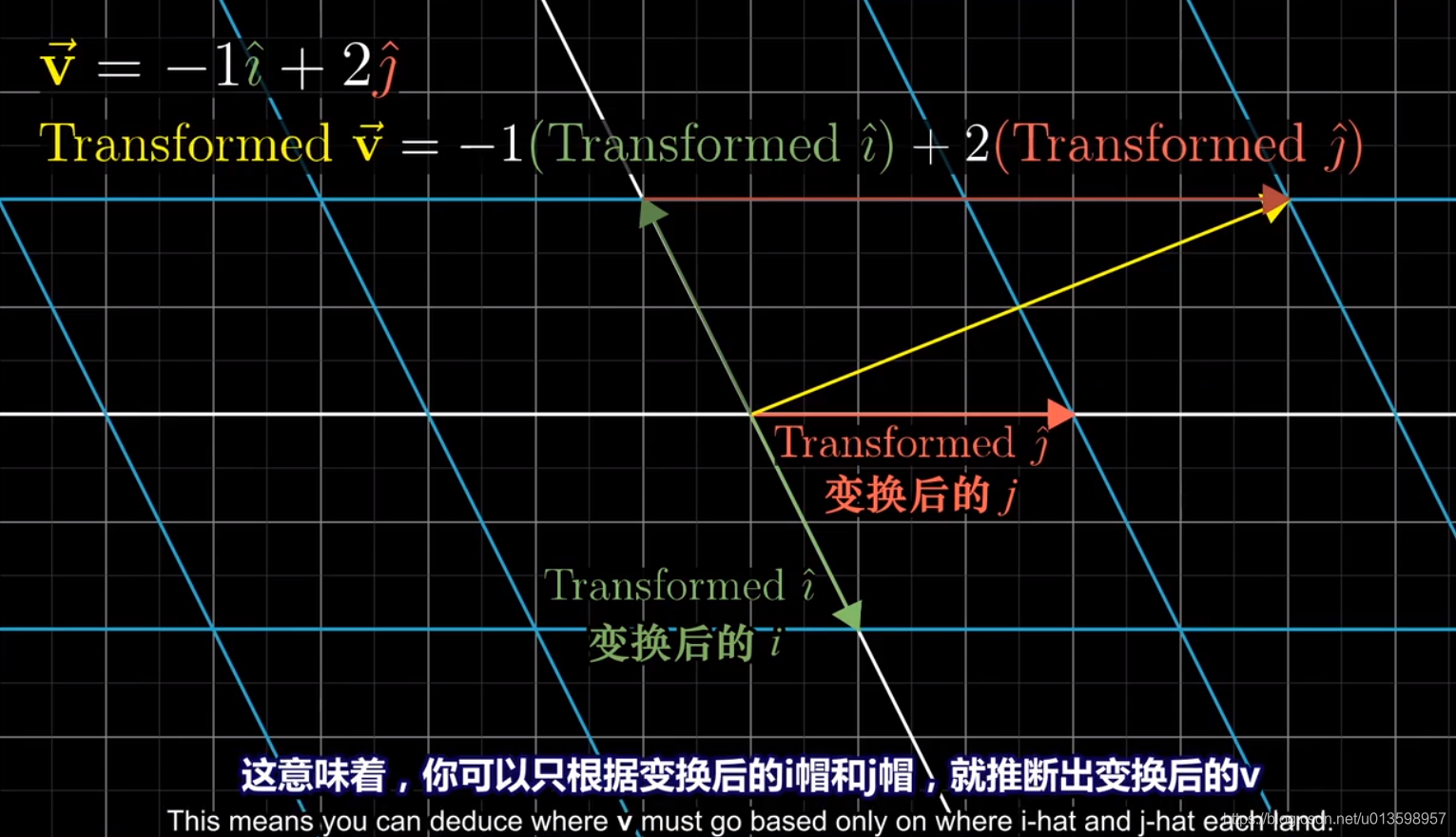
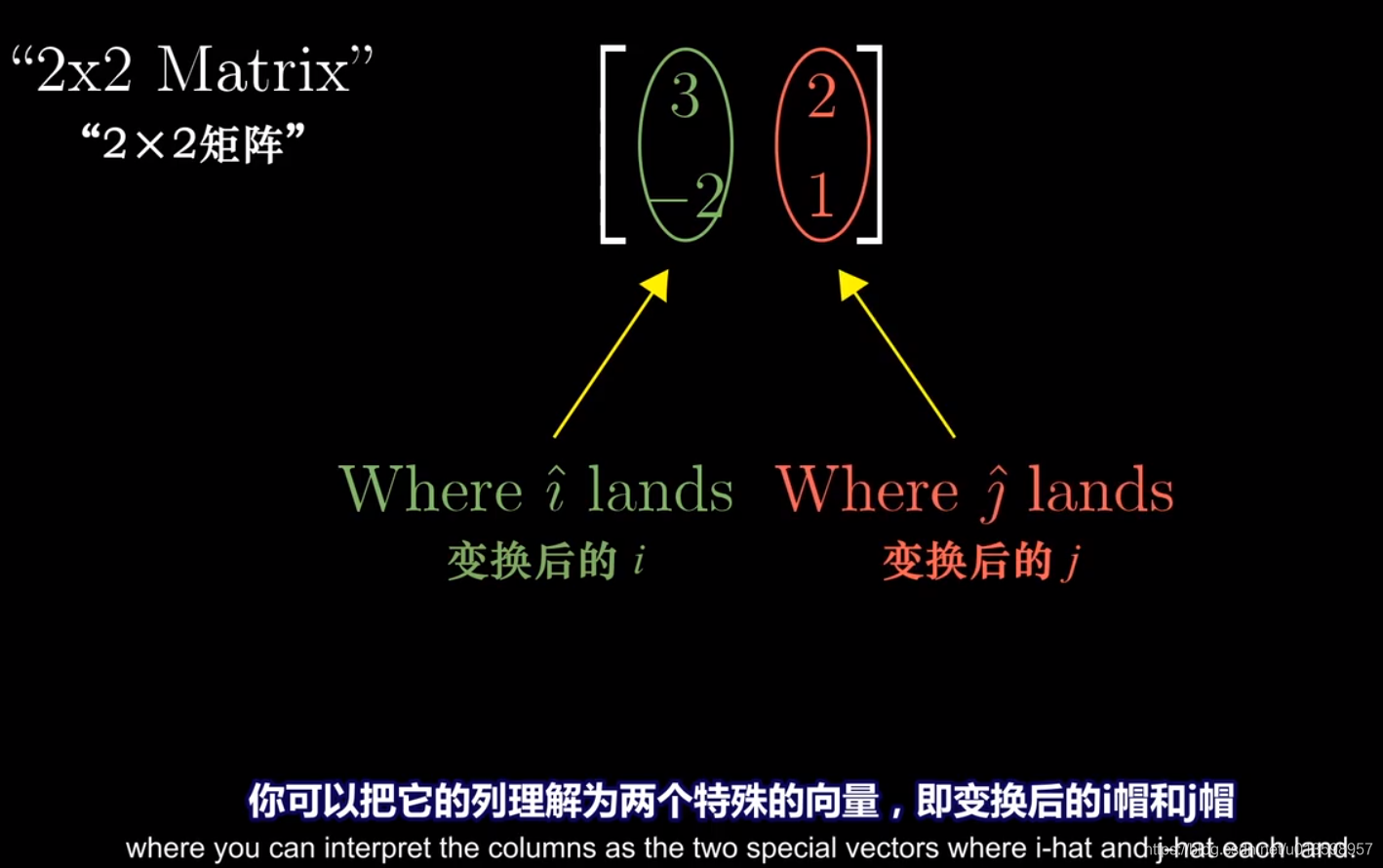
观念:可以把矩阵视为线性变换。
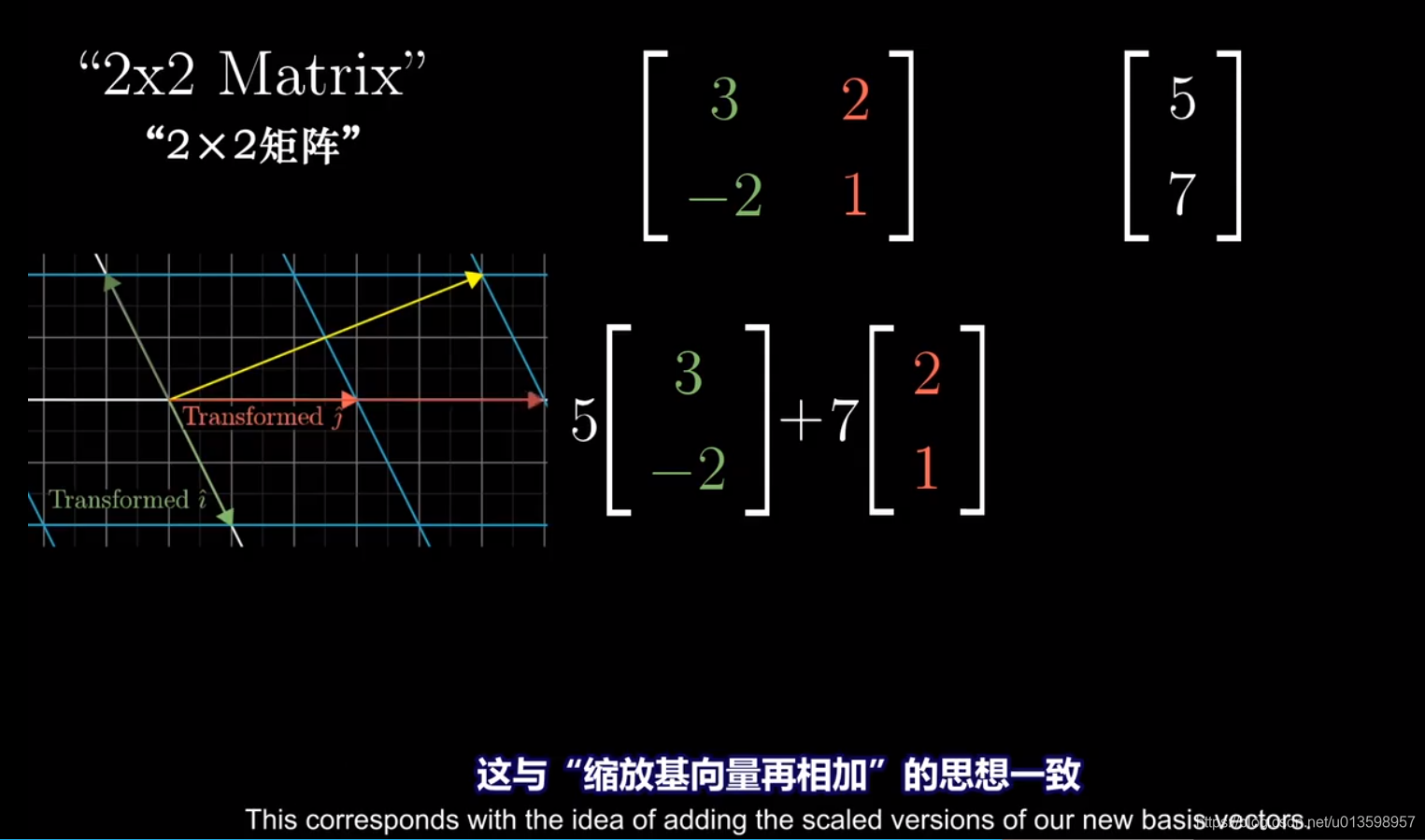
(把5和7视为缩放操作,矩阵变换视作更换基向量)
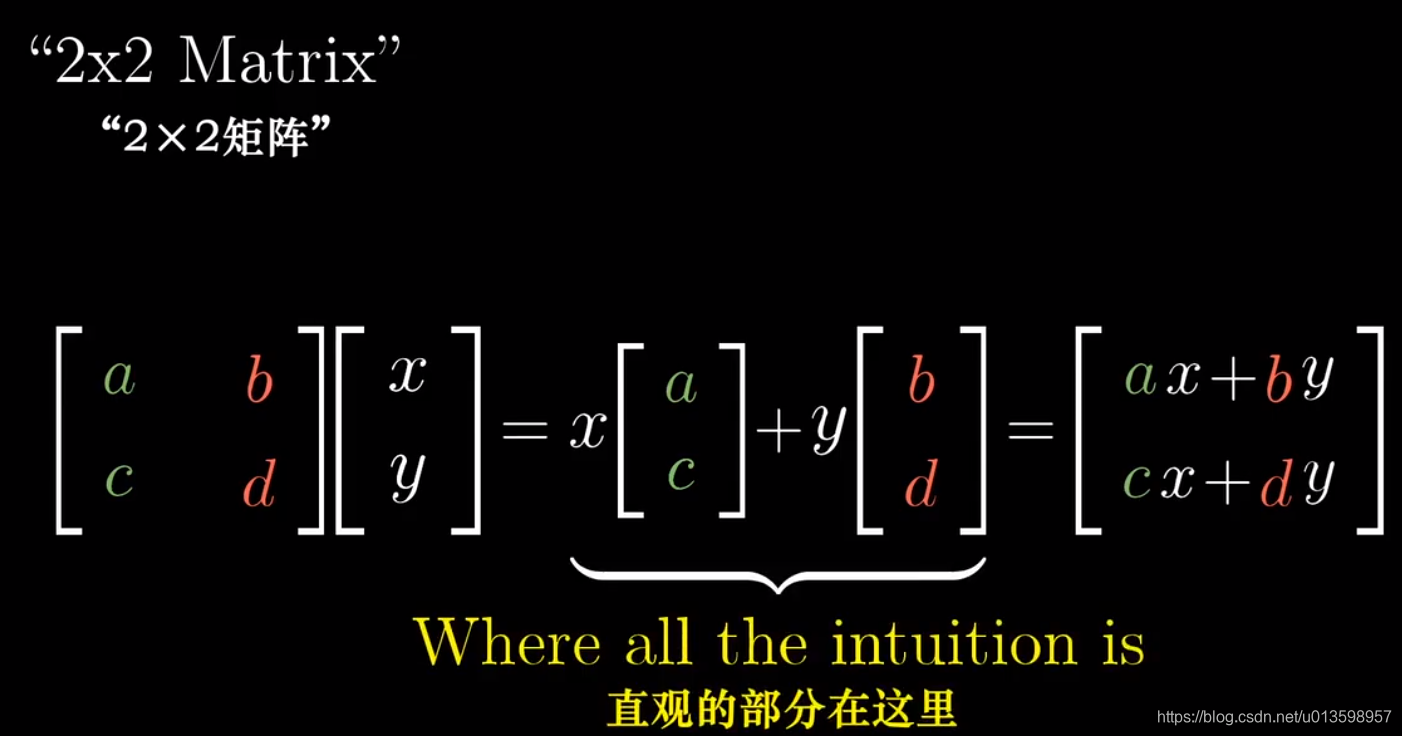
多尝试用 基向量-空间运动 去理解变换。
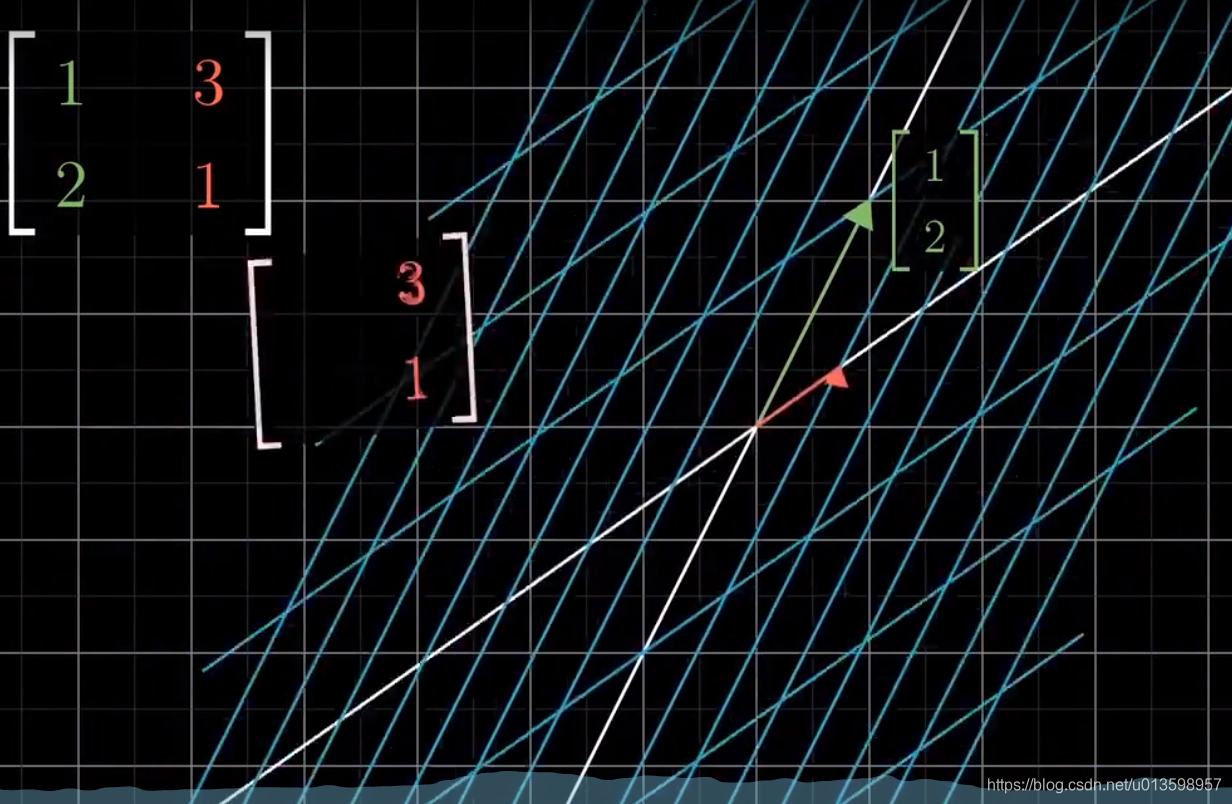
04 矩阵乘法与线性变换的联系
如“旋转剪切”这样一个新变换,可视为先旋转、再剪切这两个独立线性变换的复合变换。

注意,独立的两个变换均针对初始基向量而言!运算顺序为先右后左。
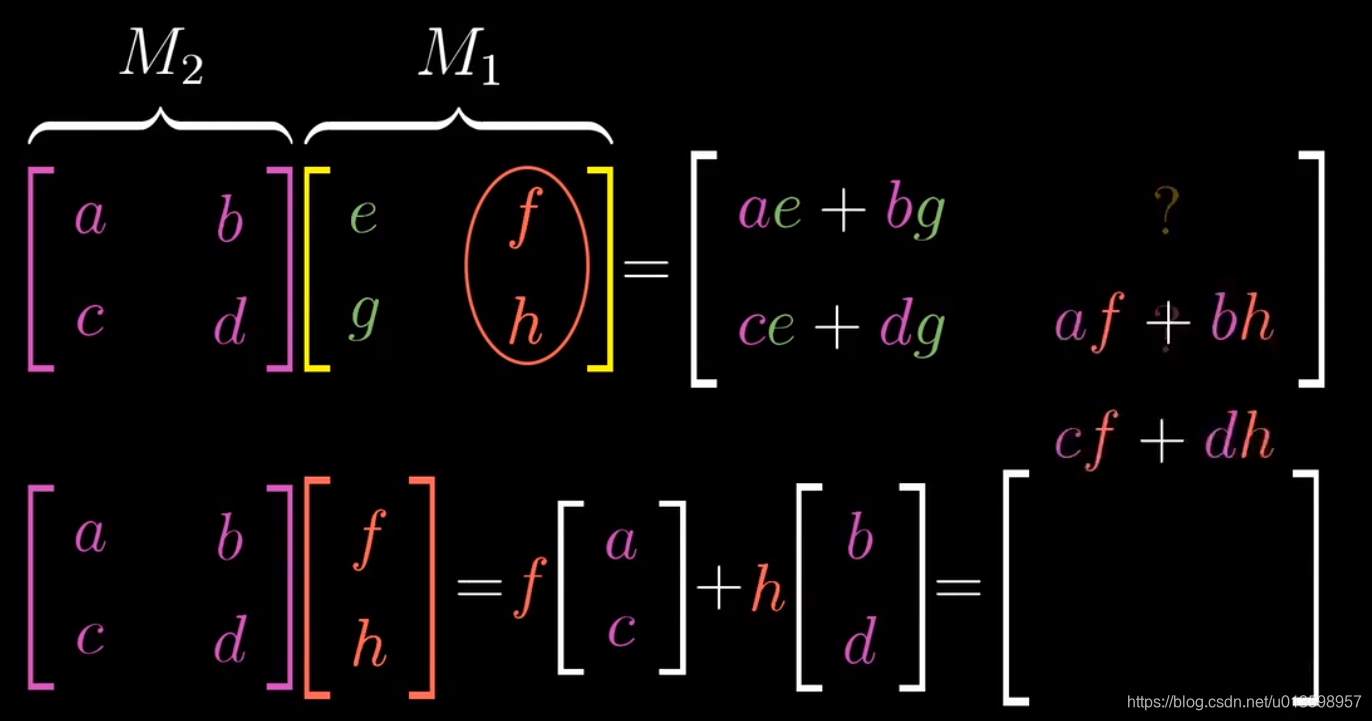
从几何直观看,显然两个矩阵的作用顺序对变换效果有影响,所以乘积顺序也如此。同理,结合律的成立在于没有影响真正的作用顺序。
05 行列式
理解线性变换,从变换对空间有多少拉伸和挤压的角度也很重要。
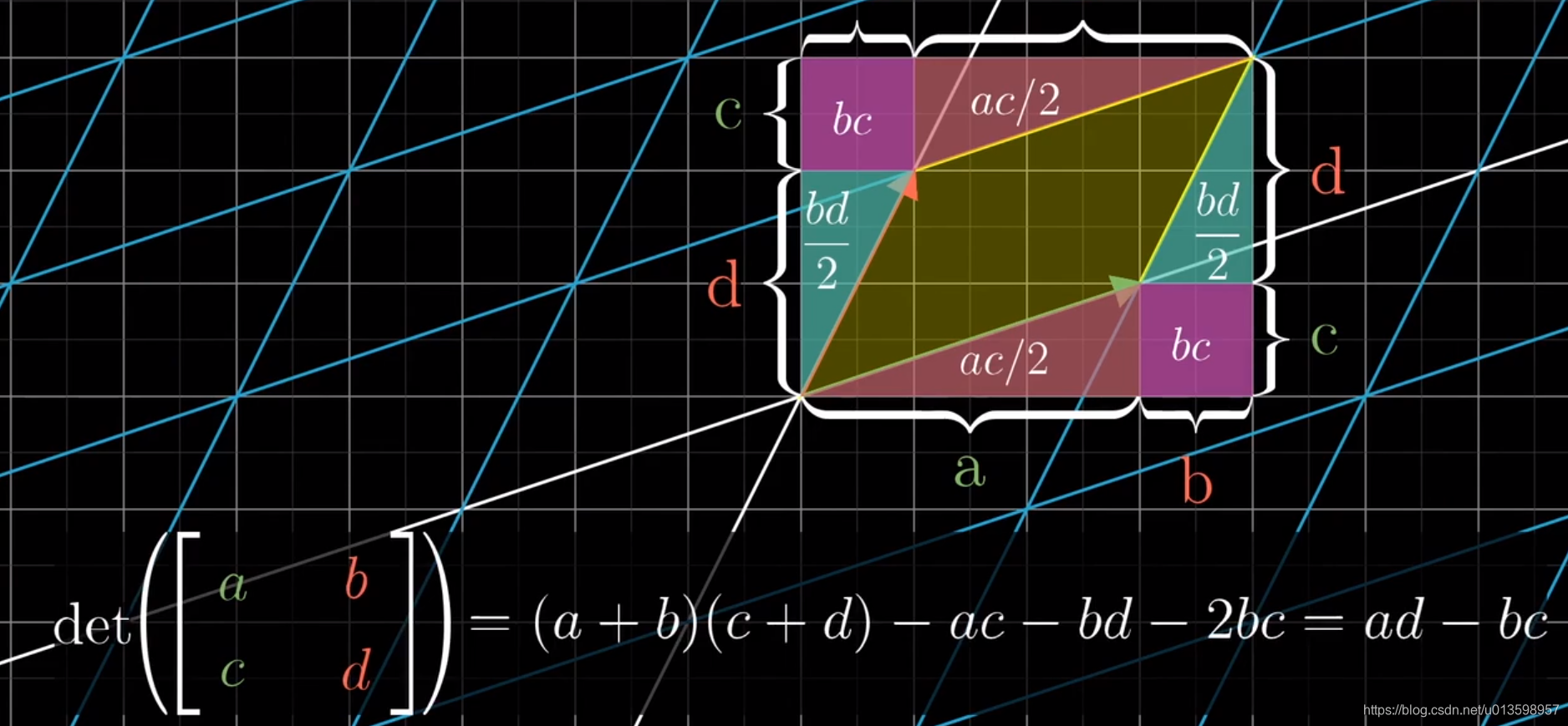
线性变换改变面积/体积/空间的比例,称为行列式。

三维矩阵的行列式为0时,表示这个线性变换将体积压缩为0,一个平面、一条直线或一个点(更小维度——也表明线性相关)。
行列式为负值的理解:如把一张纸翻转——空间定向发生改变。绝对值依然表示缩放比。
对计算,如果要从变换角度深刻理解:

06 逆矩阵、列空间、秩与零空间
首先,与线性方程组联系:

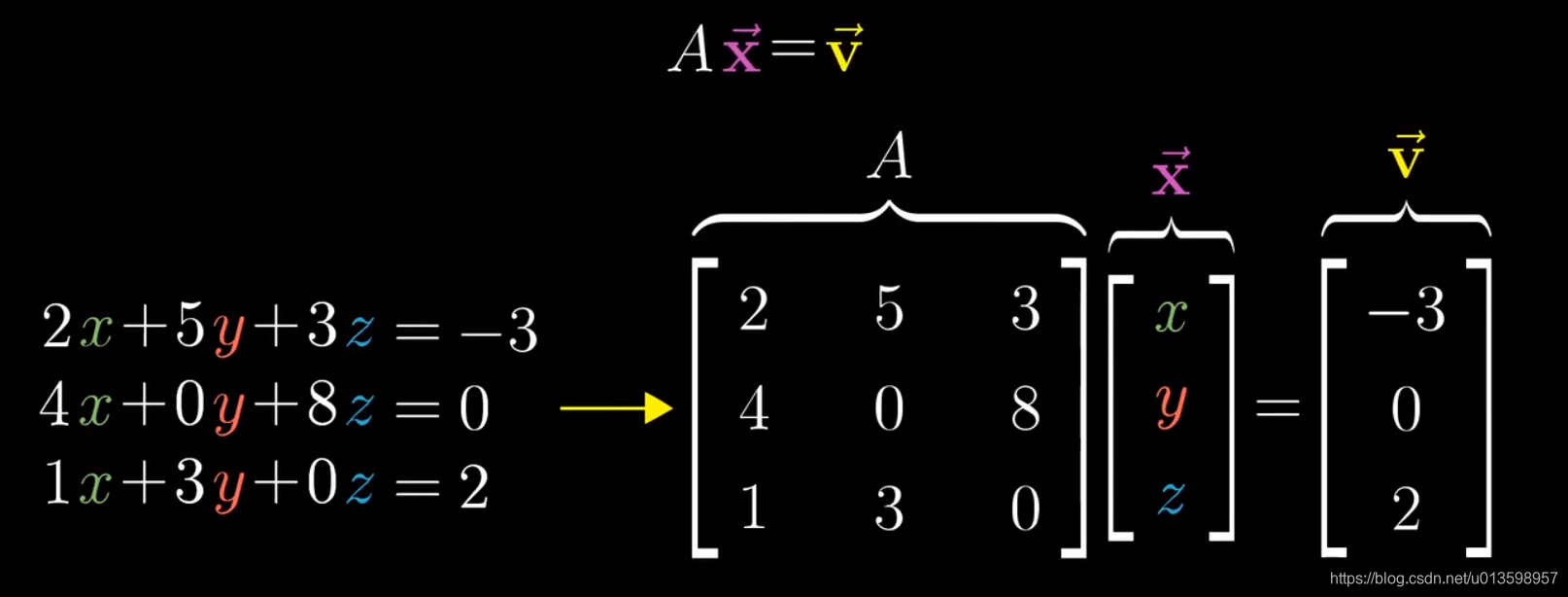
接下来,将求解与线性变换联系。首先分类讨论:行列式是否为0。
1.非零:有且只有一个向量与x变换后重合。也可以逆向变换找到x。

1.为零:不能逆向将一个单独的向量变为一整条线的向量,即应一个函数对应一个输出。

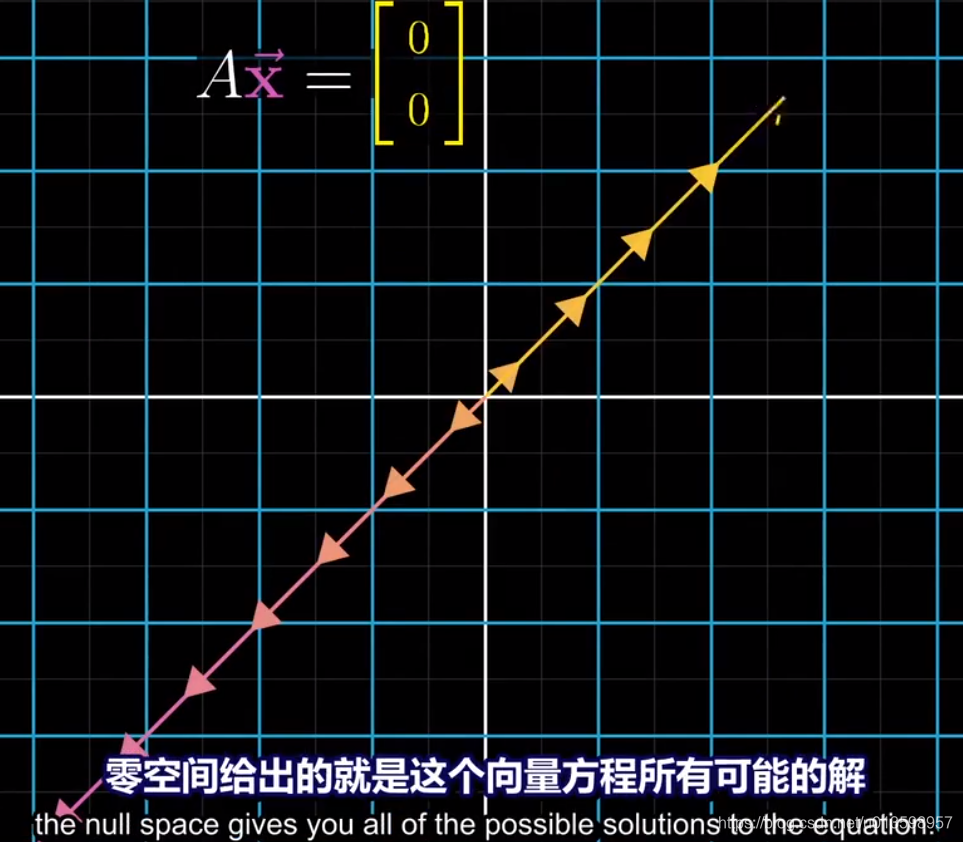
不过,这种情况下,解仍然可能存在。由此,引出秩和零空间的概念。

定义:变换后空间的维数。秩比原先减小意味着压缩。满秩:秩与列向量数相等。
零向量一定会在列空间中,因为原点保持不变。而对于非满秩矩阵,有一系列向量会变换为零向量,其集合称为“零空间”。
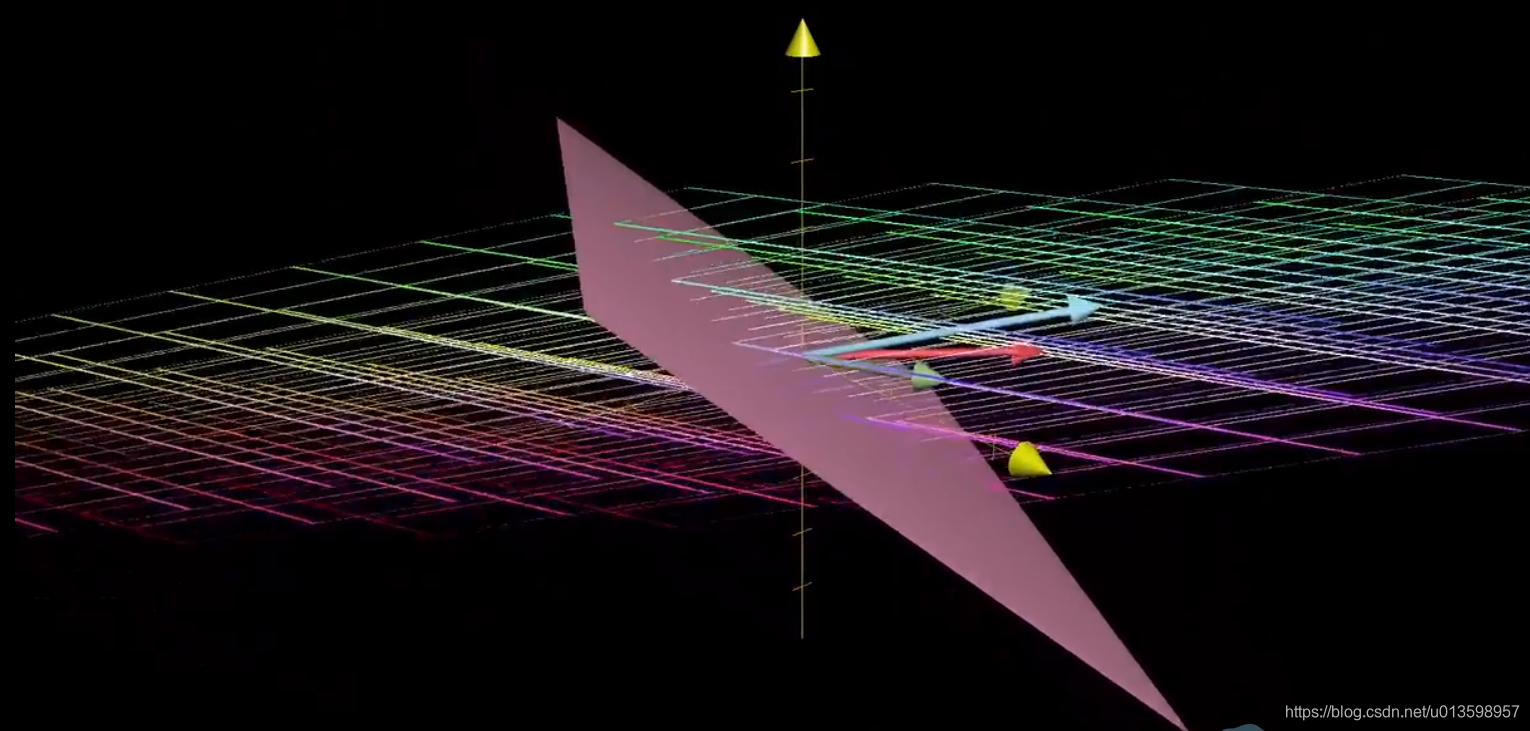
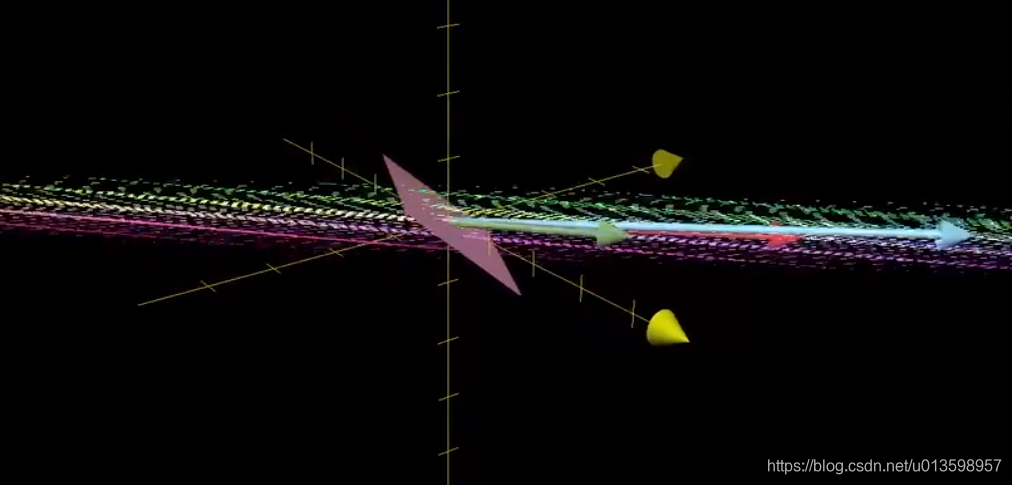
(例子:三维空间压缩为直线,相当于一个平面被压缩为0向量)
补充:非方阵 不同维度之间的线性变换
以3 * 2矩阵为例,可以理解为是将二维空间映射到三维空间,2 * 3则是则是三维到二维。
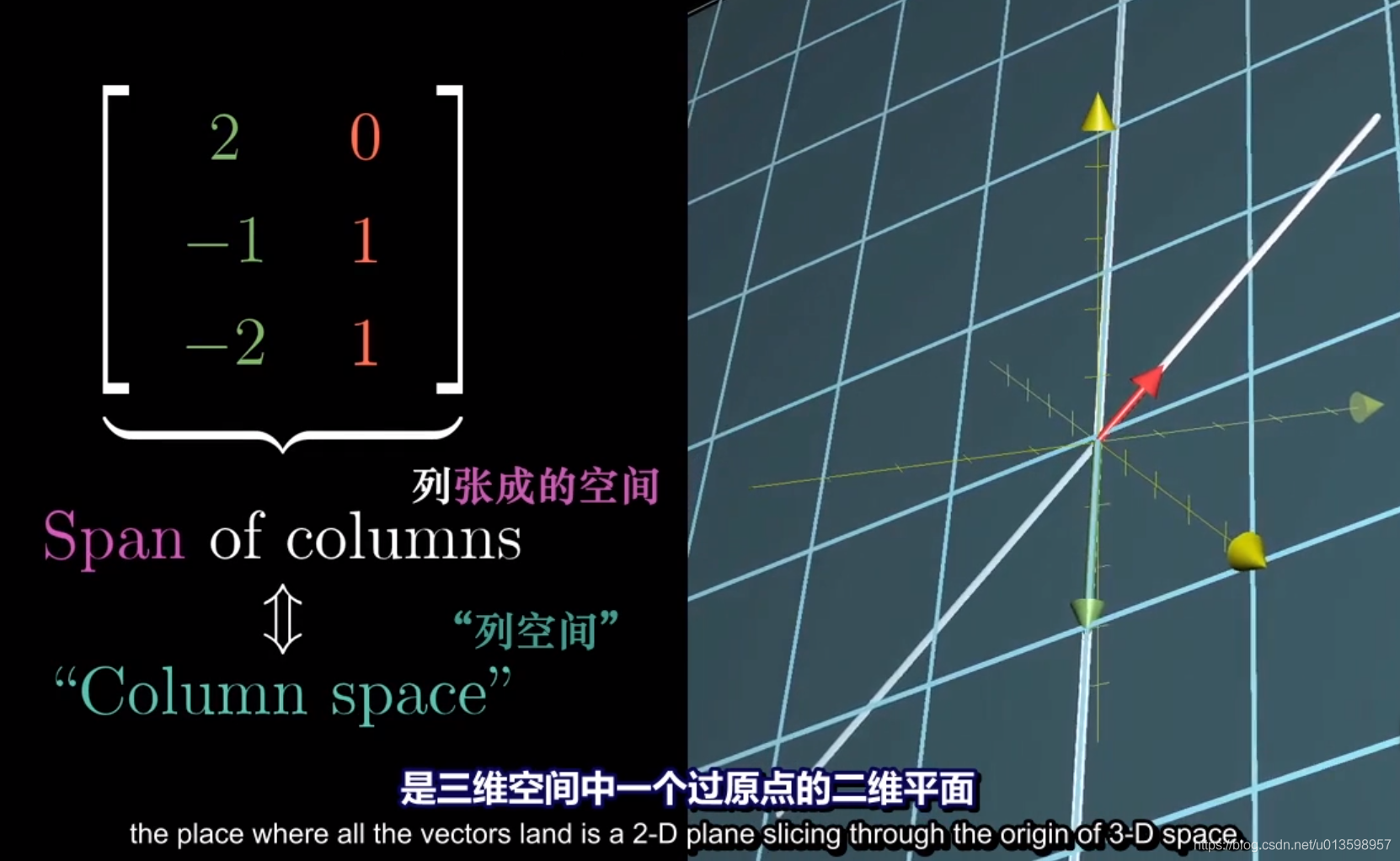
(矩阵依然满秩,输入列向量数目=真正覆盖空间维度)
07 点积与对偶性
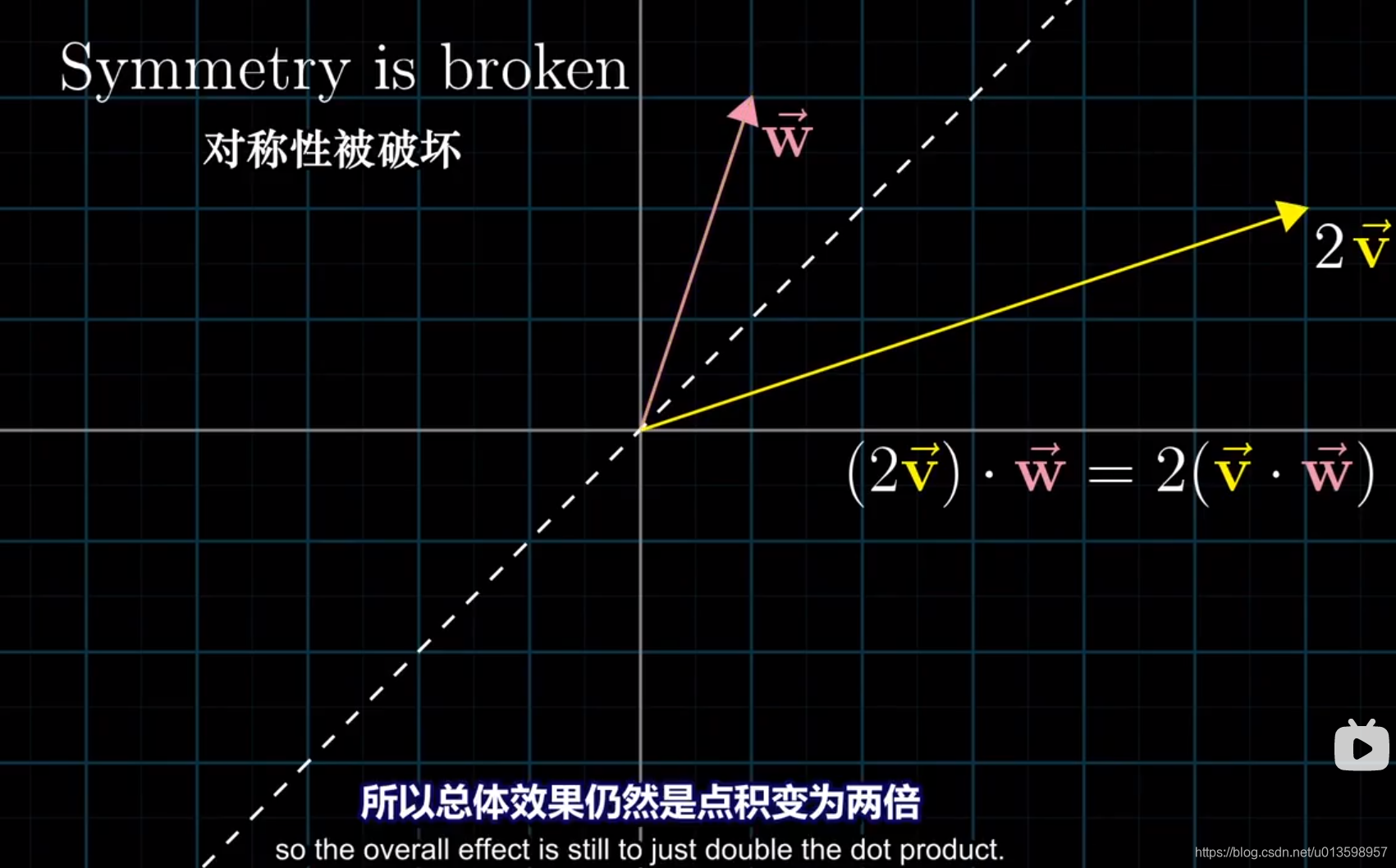
传统几何解释:点积 是一个向量在另一个向量方向上投影的长度与另一个向量长度的乘积。

点积与向量顺序无关的理解:
矩阵变换与点积相联系:
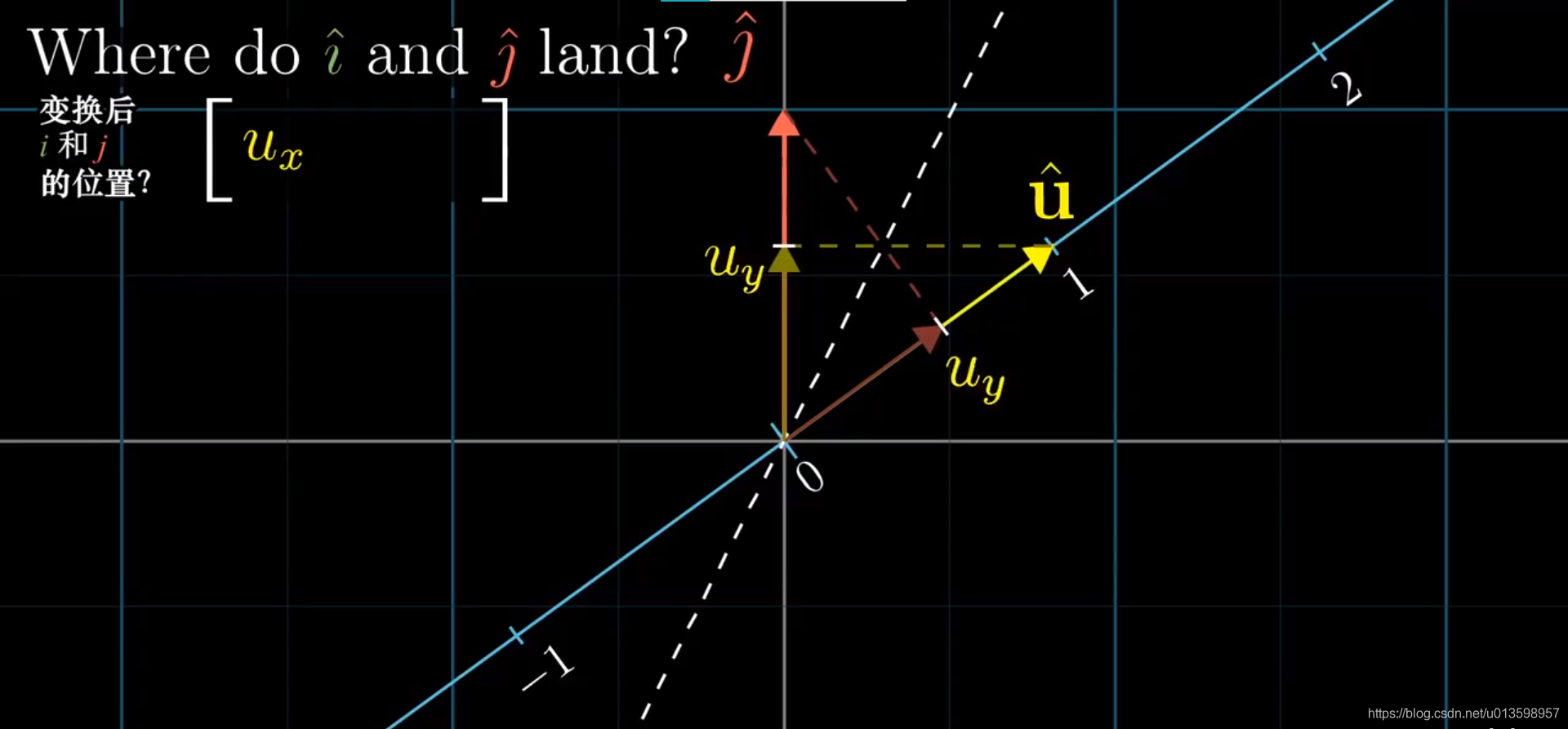
对上面这张图片的理解:原本ux,uy所在的1* 2矩阵应视为线性变换,现在利用转换,将其变为2* 1矩阵,或者说是 二维向量u ,同时巧设转换得到的u所在方向为压缩变换的方向。接下来,利用投影对称,同时结合矩阵变换和向量投影,进一步探索联系。

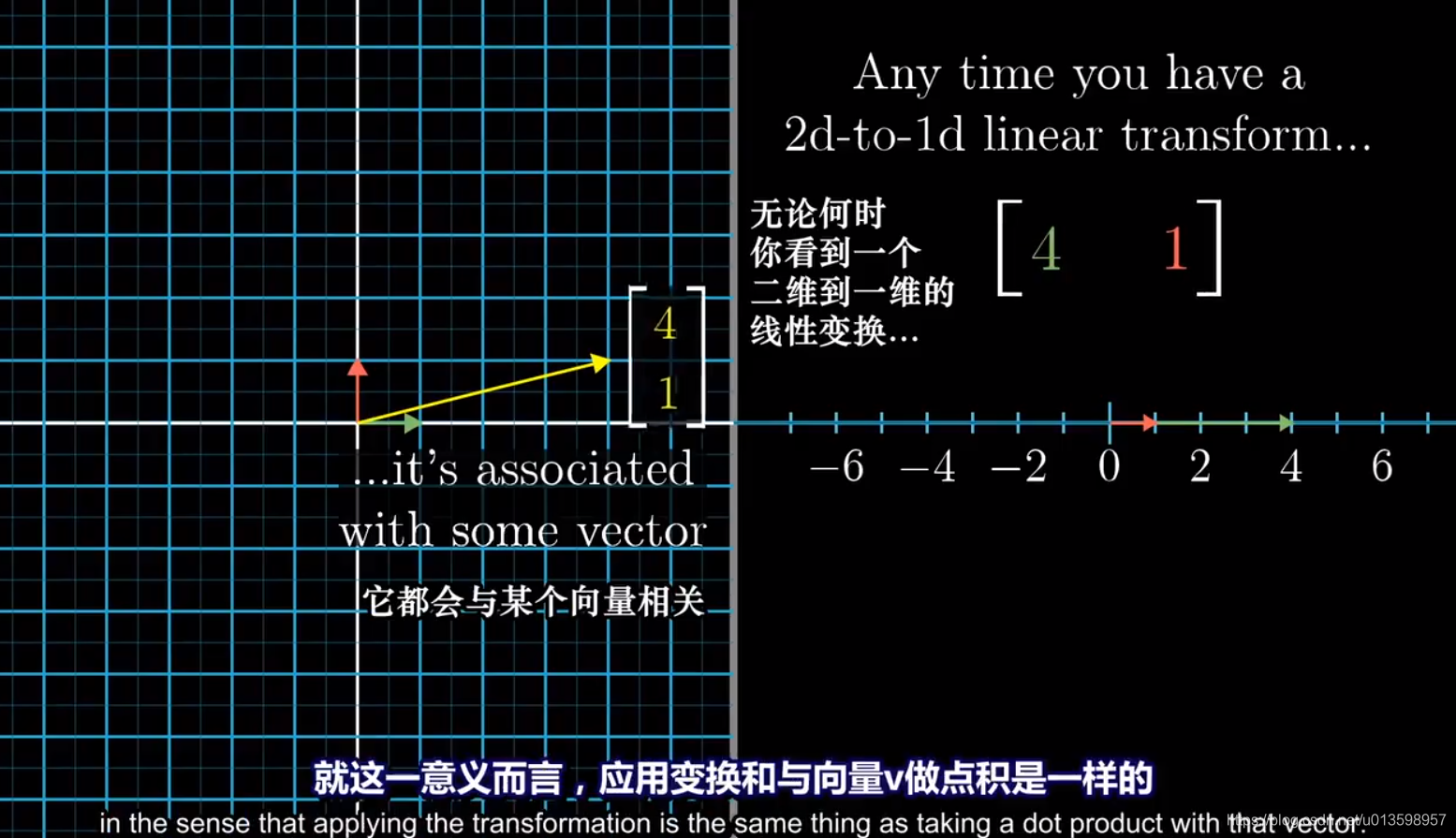
可以认为,一个多维空间的线性变换的对偶是多维空间中的某个特定向量。
对偶性:
08 叉积
传统介绍:
叉积表示两个向量的有符号面积值(行列式),也表示垂直于两个向量的另一个向量(应该说这才是真正的叉积)。
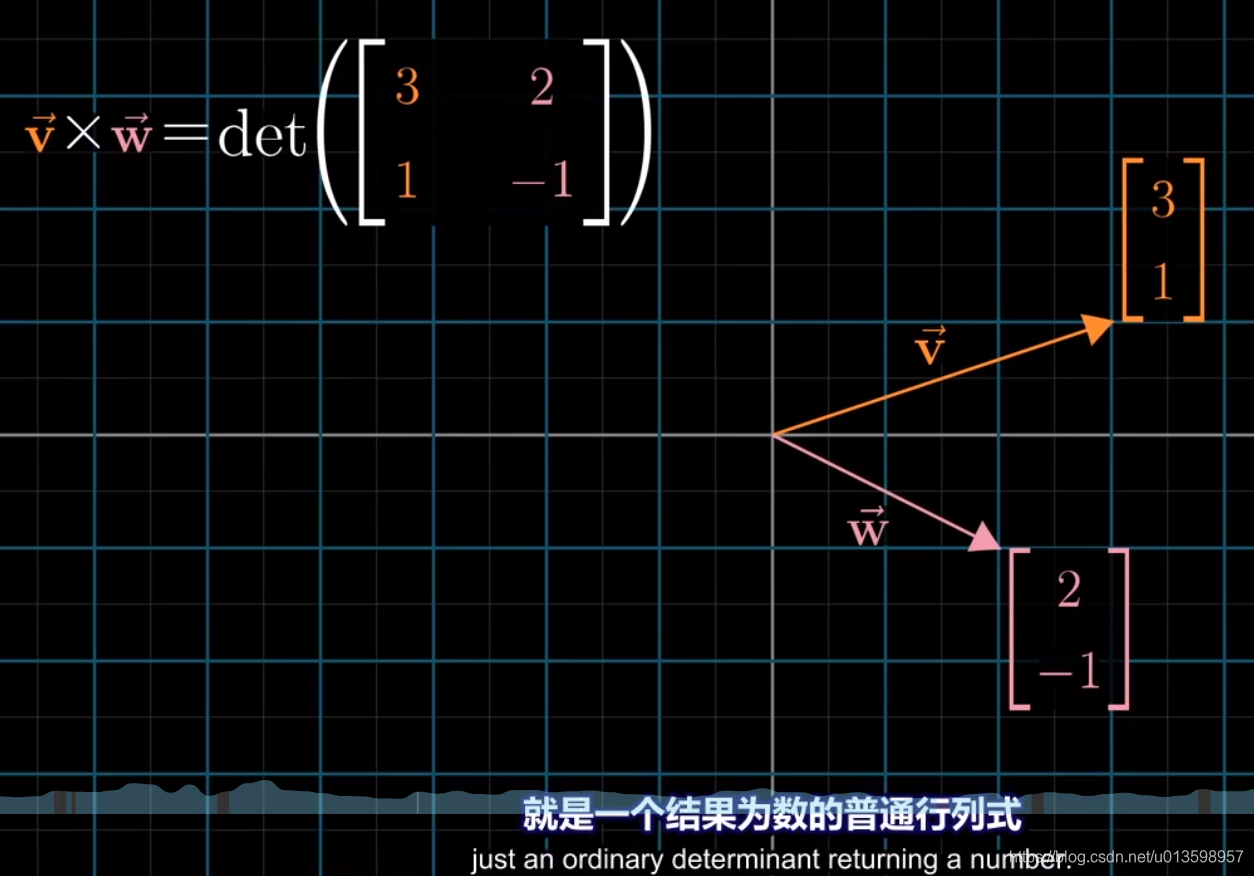
可以认为,基向量的顺序就是定向的顺序,相反则为负。

再借助一点几何直观,当两个向量夹角相接近时,其叉积得到的绝对值也越小。
叉积作为二元运算,推广至三维向量:
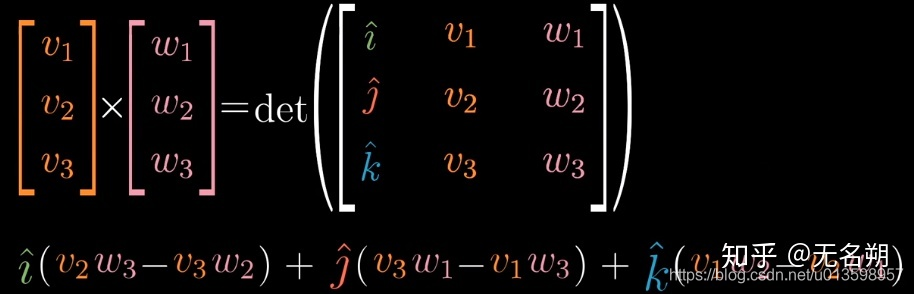

这里的第一列为什么是单位向量,怎么理解?后面在本质介绍的环节会给予解释,但解释时,先带着这样的运算公式进行推导,以求得到最终相应。
通过对偶性,从本质介绍:
回顾对偶性思想,其在于一个多维空间到数轴的线性变换与那个空间唯一一个向量对应。应用这个线性变换与向量点乘一致。
Plan:

头脑风暴来了:
先想到函数,引入输入向量。于是建立三维到一维变换函数的假设,已知两个问题下的向量,输入一个向量(新引入的)。

把函数思想放到线性代数的场景下:

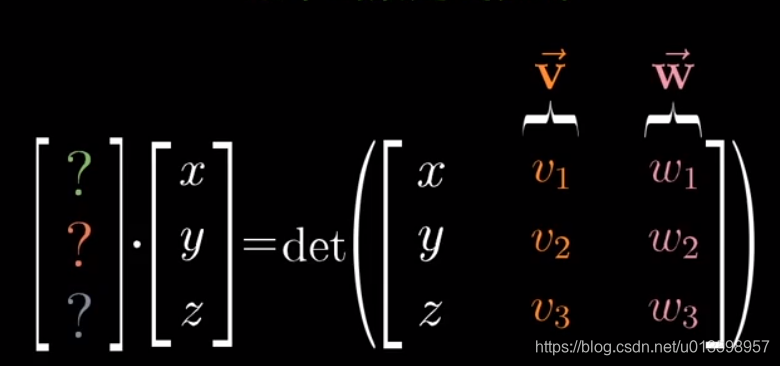
于是,现在要求出这个未知向量,设为p。
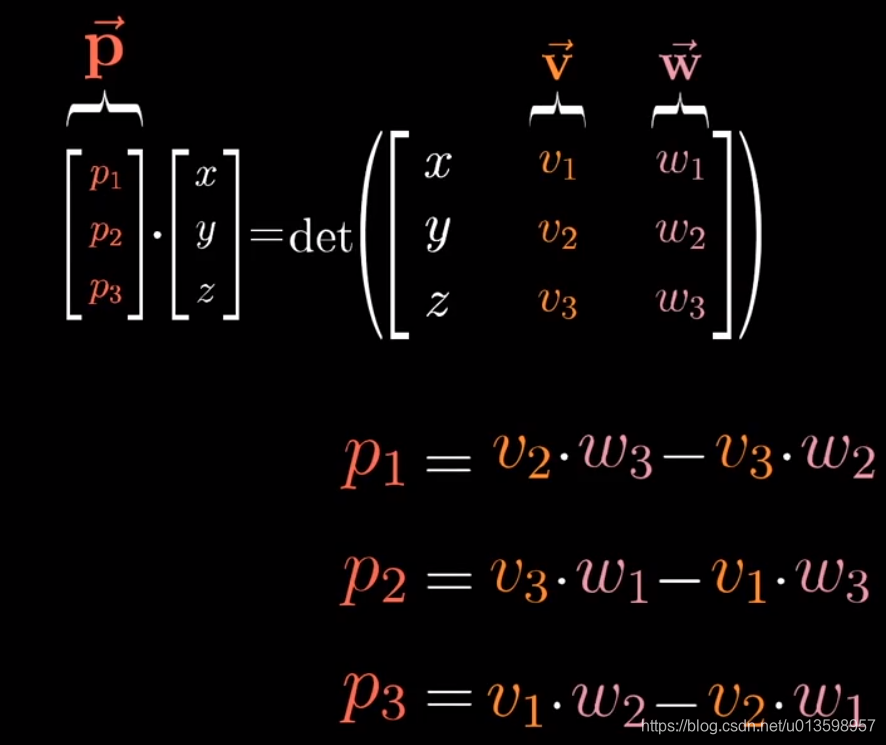

把i,j,k分别代入x,y,x,发现上图点乘数值结果与两个向量叉积一样。
因此,当p与某个向量(x,y,z)点乘后得到的结果,相当于这个向量(x,y,z)与原有的两个向量V、W构成的平行六面体的有向体积。

再通过点积的几何解释(投影),继续探索。
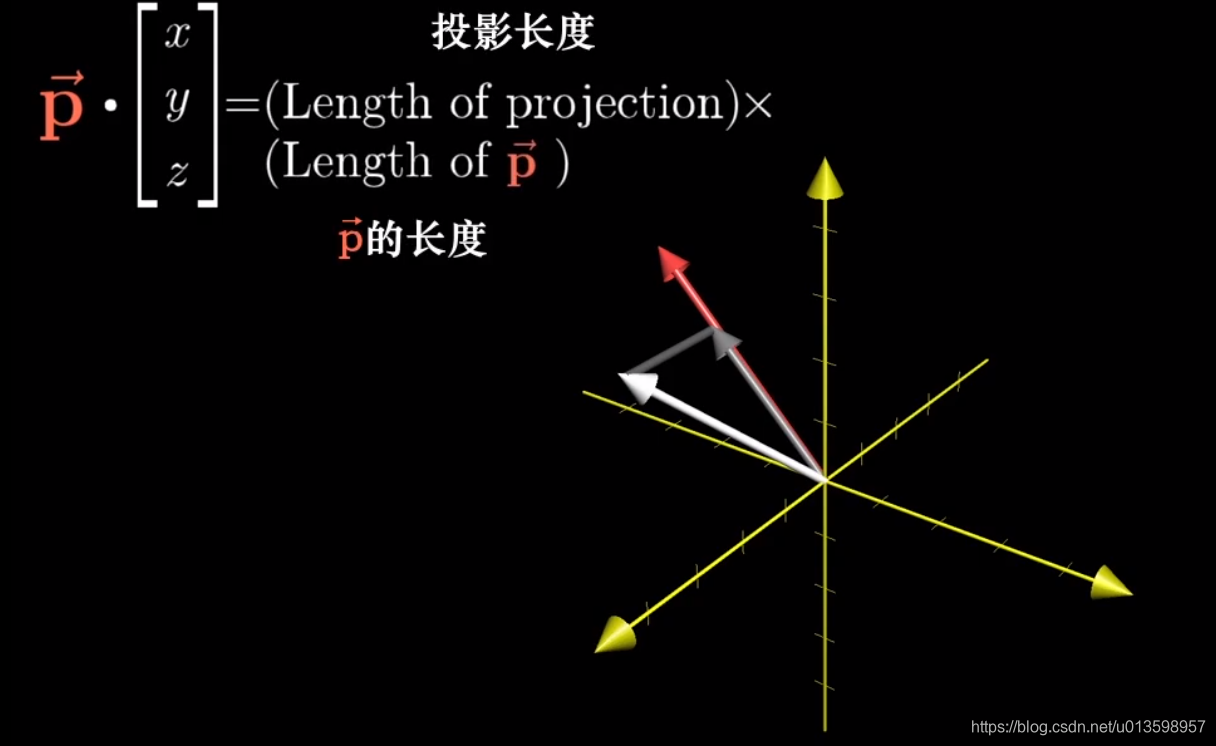

思维转弯有点反应不过来。。:

(点乘的几何意义也要深刻理解。。)
09 基变换
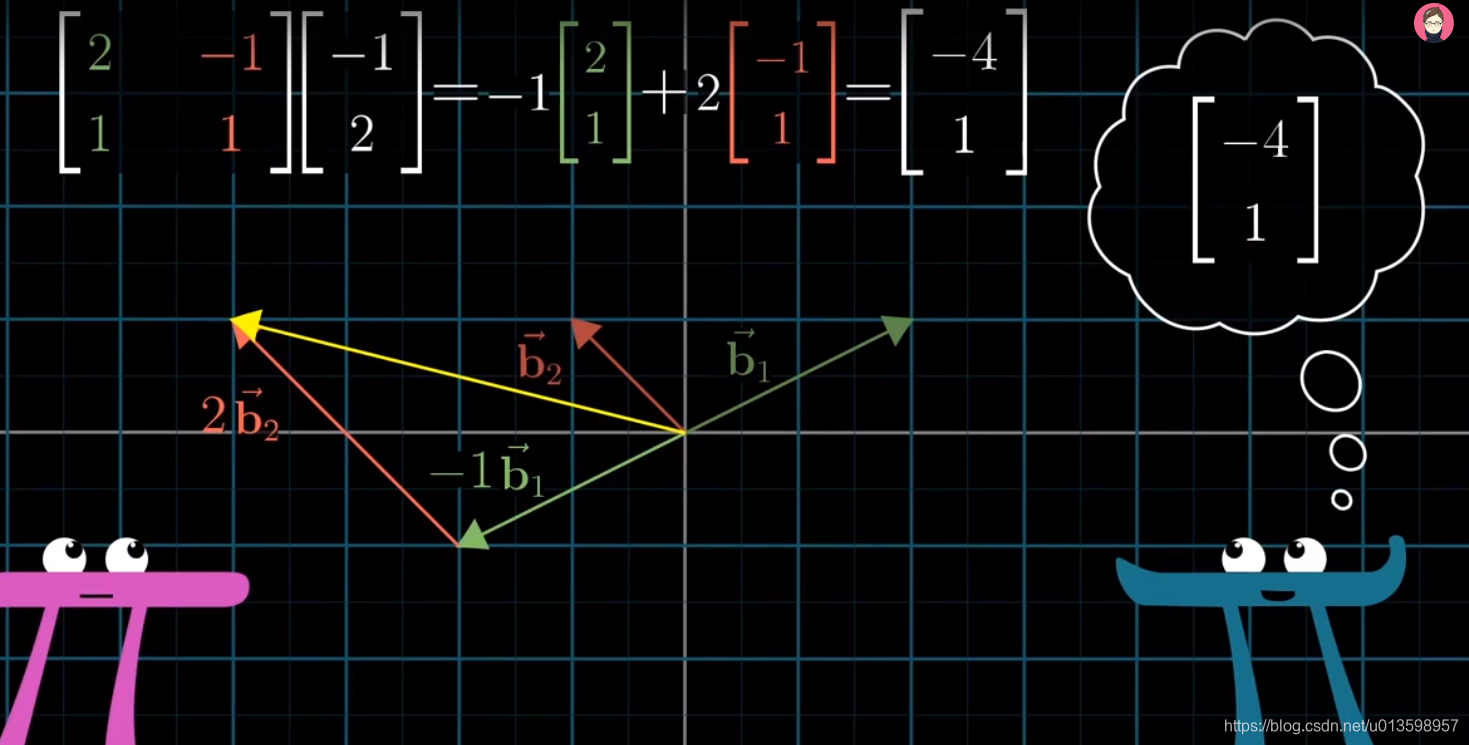
! 将矩阵向量乘法的变换 与 缩放基向量联系。
“颠倒”的感觉:
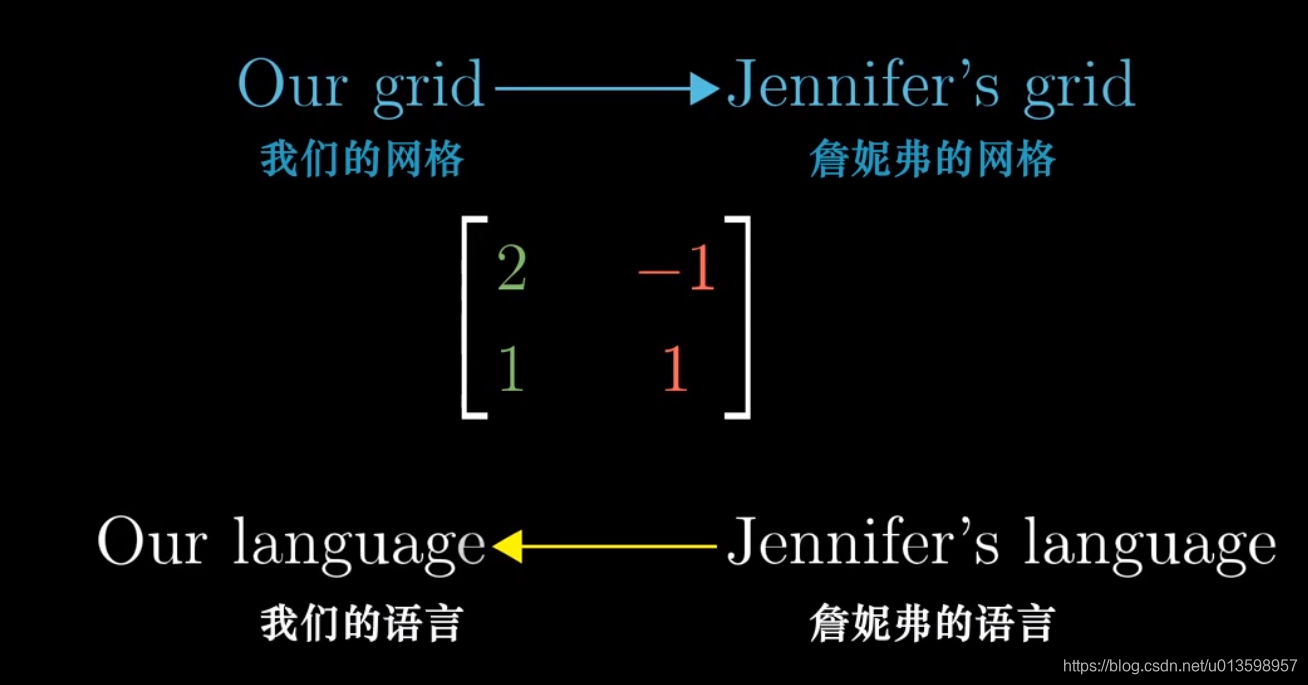
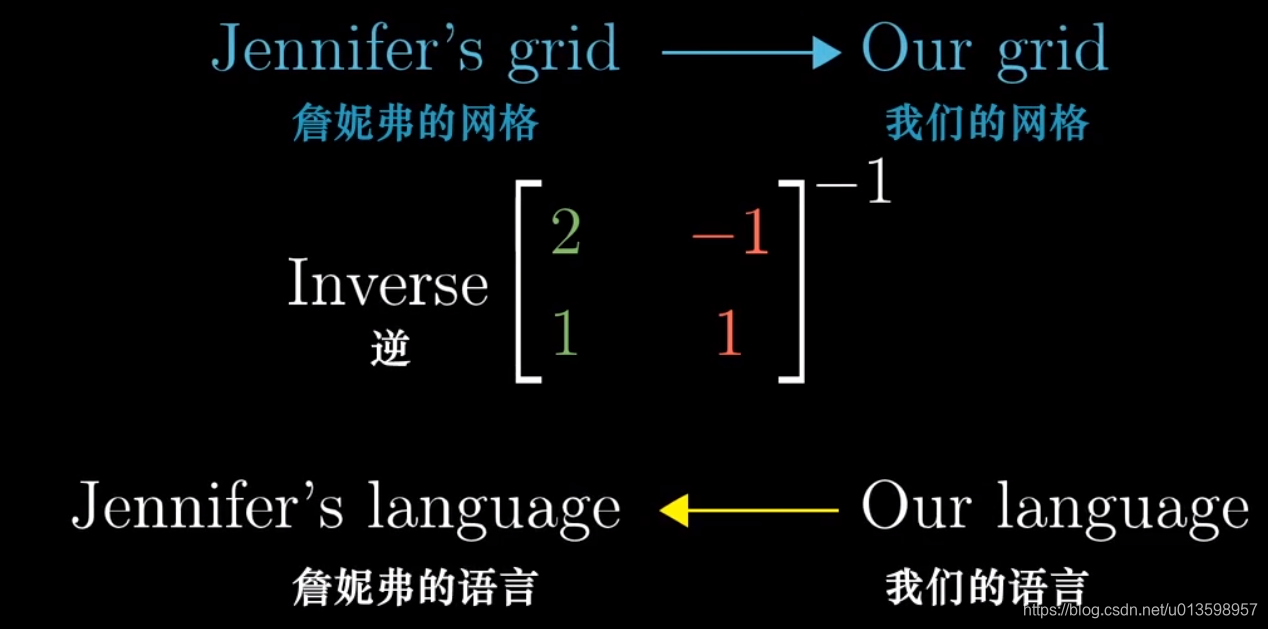

矩阵转换:

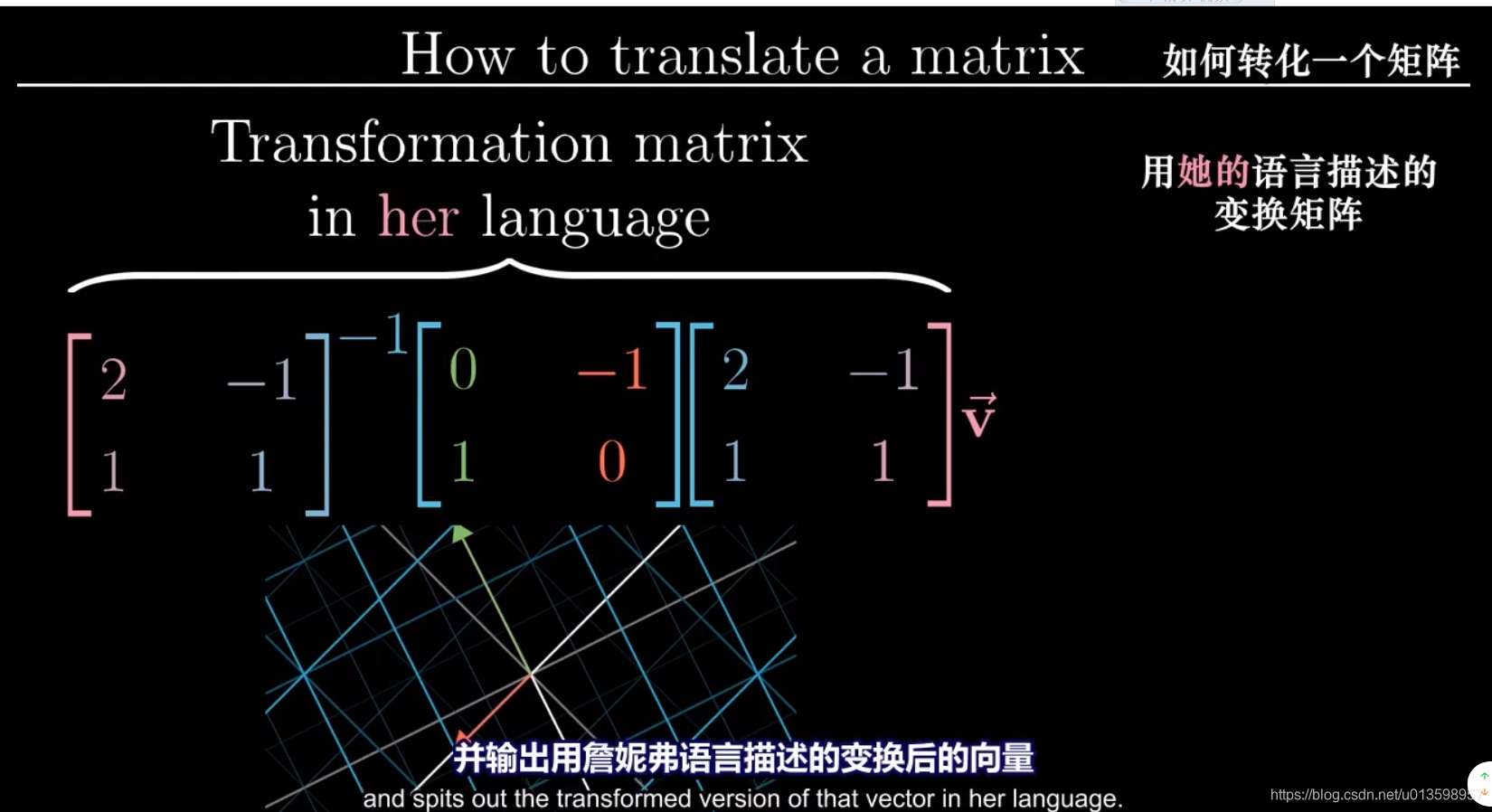
可以这样理解左式中间,矩阵变换的描述要用同一种语言。
因而最后一步左乘矩阵是基变换矩阵的逆。
左式复合后的得到的2*2矩阵和变换效果,仍是逆时针旋转90度:
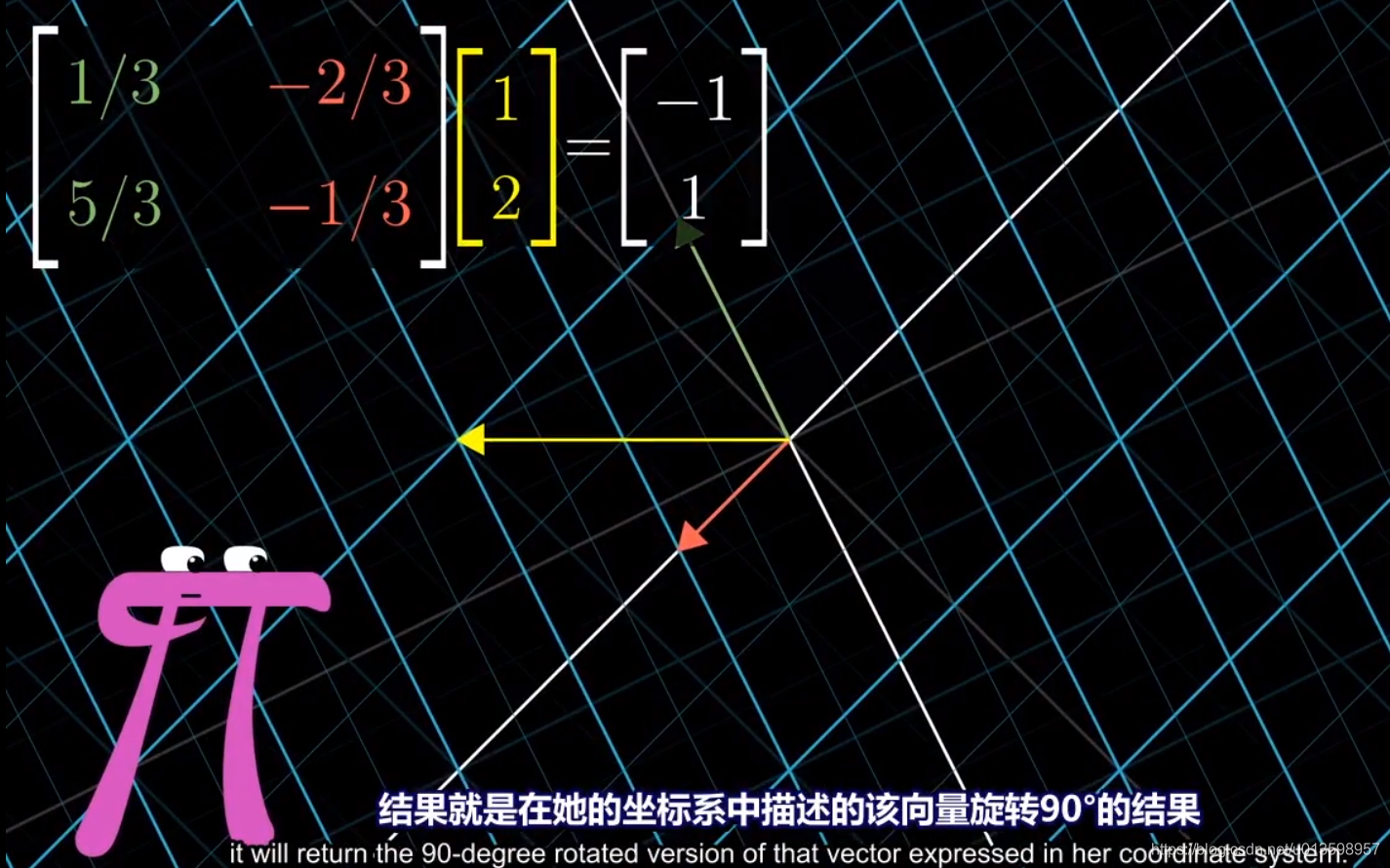

中间的矩阵代表自己所见的变换,外侧矩阵代表转移作用(视角上变化)。这个矩阵乘积仍然代表同一个变换,只不过是从其他人的角度来看。
10 特征向量与特征值
要理解本次讲的内容,需要对之前的基础熟悉了解:


一般来说,一个矩阵变换作用于一个向量,该向量的张成空间会发生偏移。
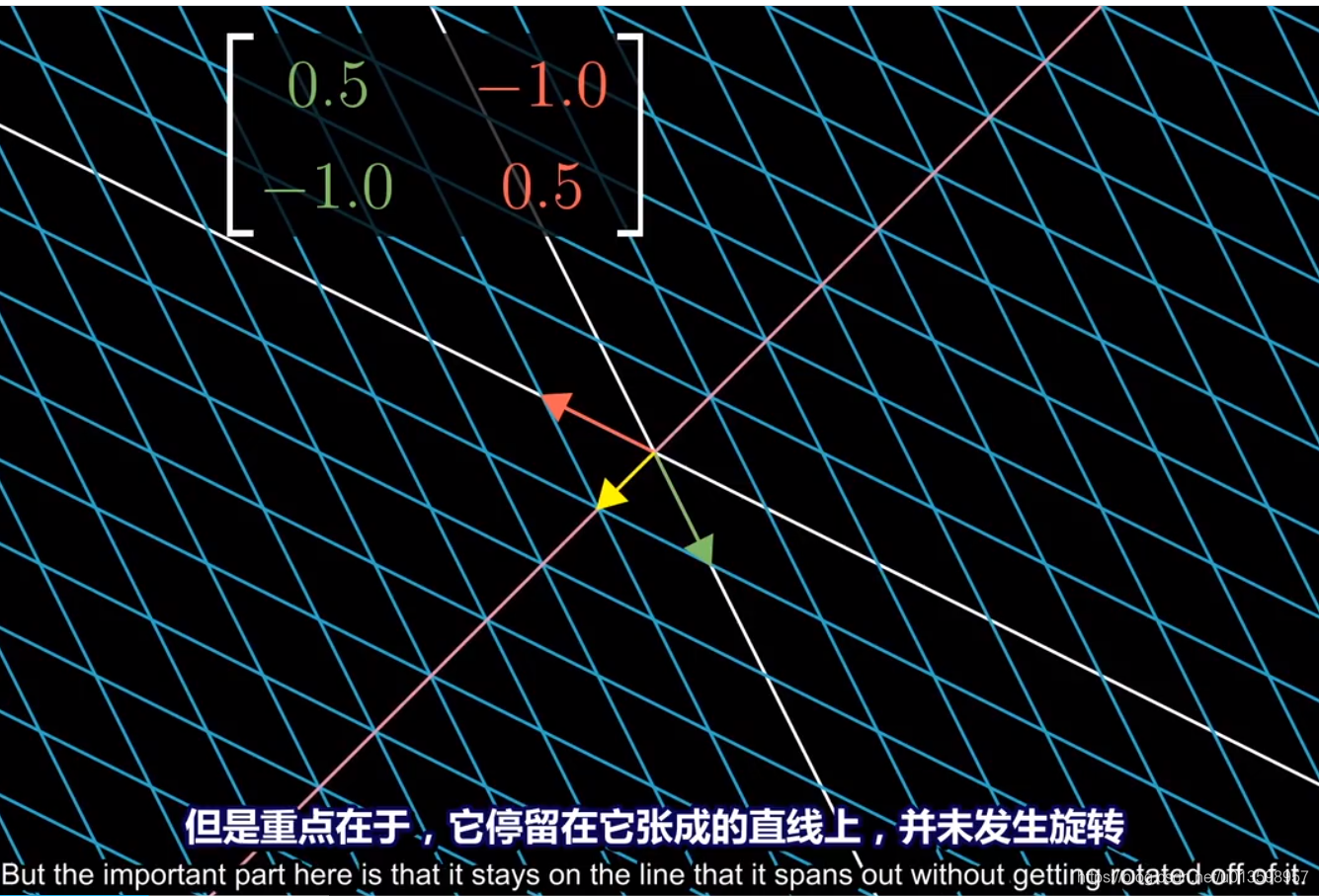
当然,也有停留情况:

上图,还有绿色基向量所在方向的向量未偏移。
推论:对于未发生偏移的向量,其所在方向对角线上的其他向量也未发生偏移。
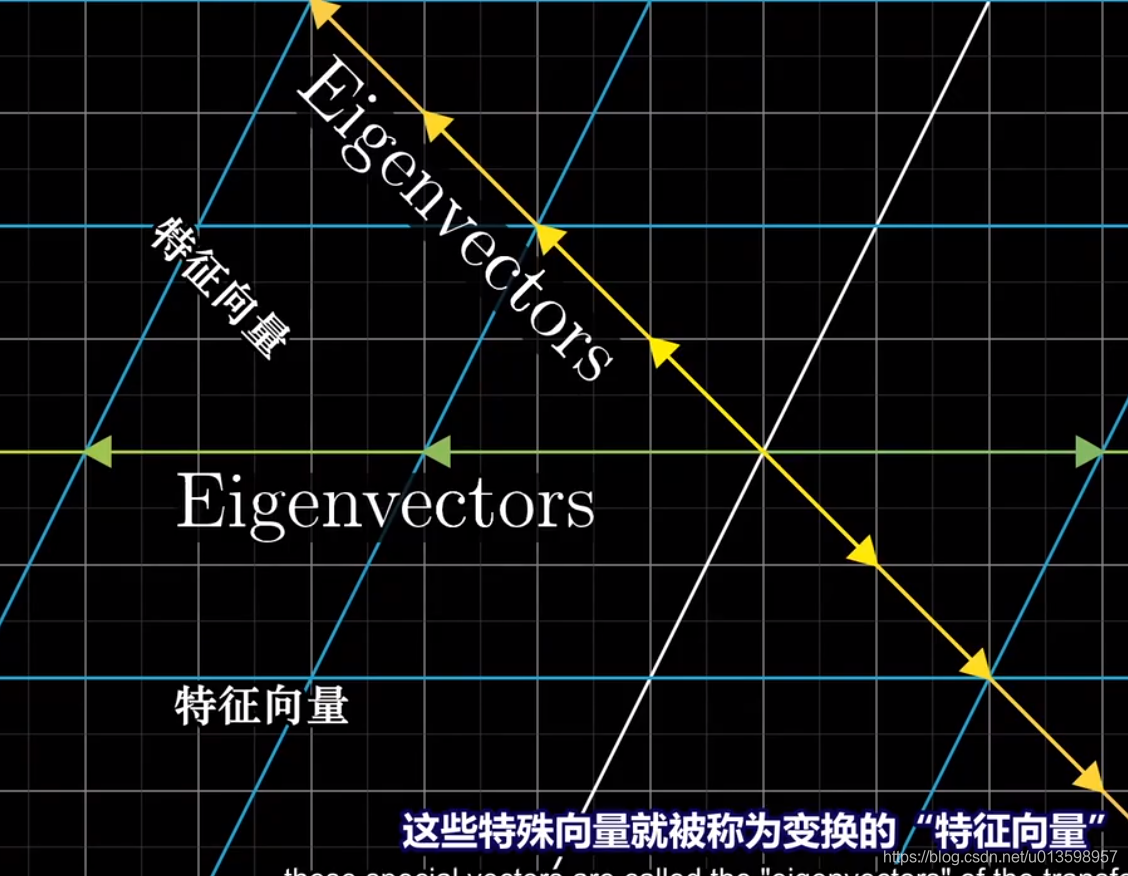
定义:变换后未离开原来张成方向上直线的向量为特征向量。每一个特征向量都有对应的特征值,来衡量特征向量在变换种中拉伸或压缩的比例。
对于特征值为负的情况:
三维空间的一个应用——三维旋转:
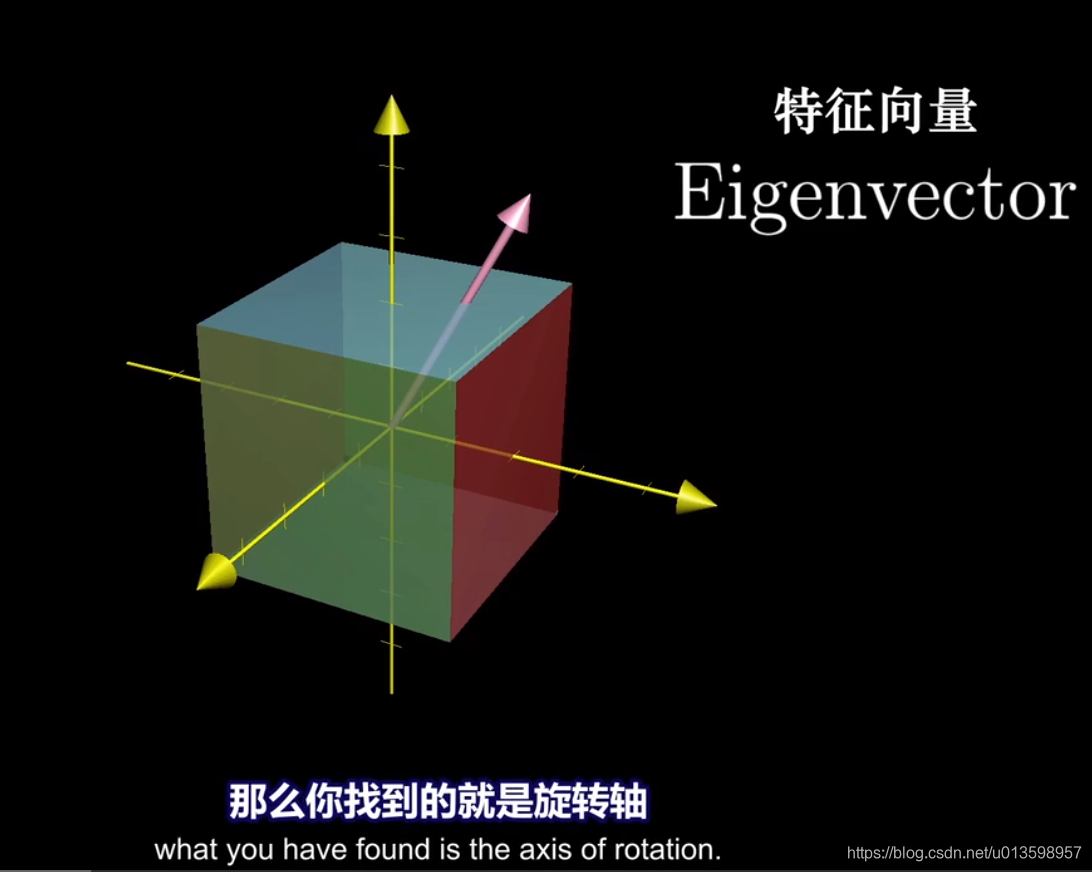
这种情况下,相应的特征值为1,且不难意识到,把这个变换看成绕轴旋转一定角度,比考虑相应的3*3矩阵要容易得多。
对于用特征向量和特征值理解线性变换:

更好的方法是求出特征向量和特征值。

λ为特征值,v为特征向量,现介绍求解。

为便于求解,先将右侧λ转换为矩阵。

如果v本身就是零向量的话,等式恒成立,但我们想要的是非零向量。
回顾之前讲的,当且仅当矩阵变换表示空间压缩到更低维度时,才会存在一个非零向量,使得矩阵和他的乘积为零向量。 空间压缩,则矩阵变换对应的行列式为0。
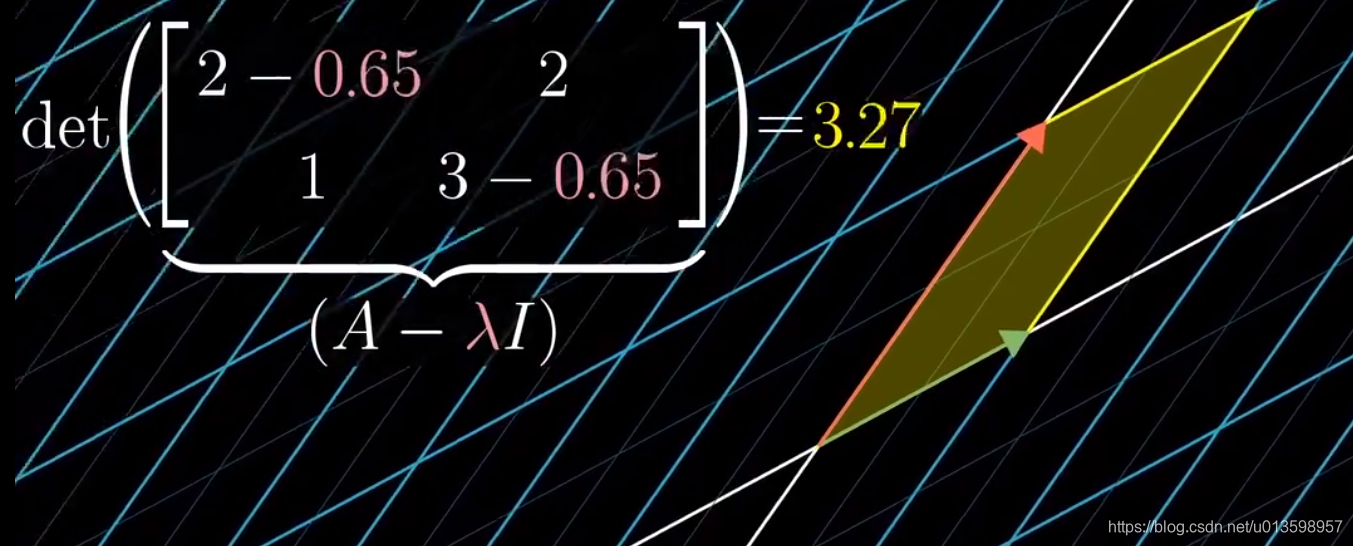
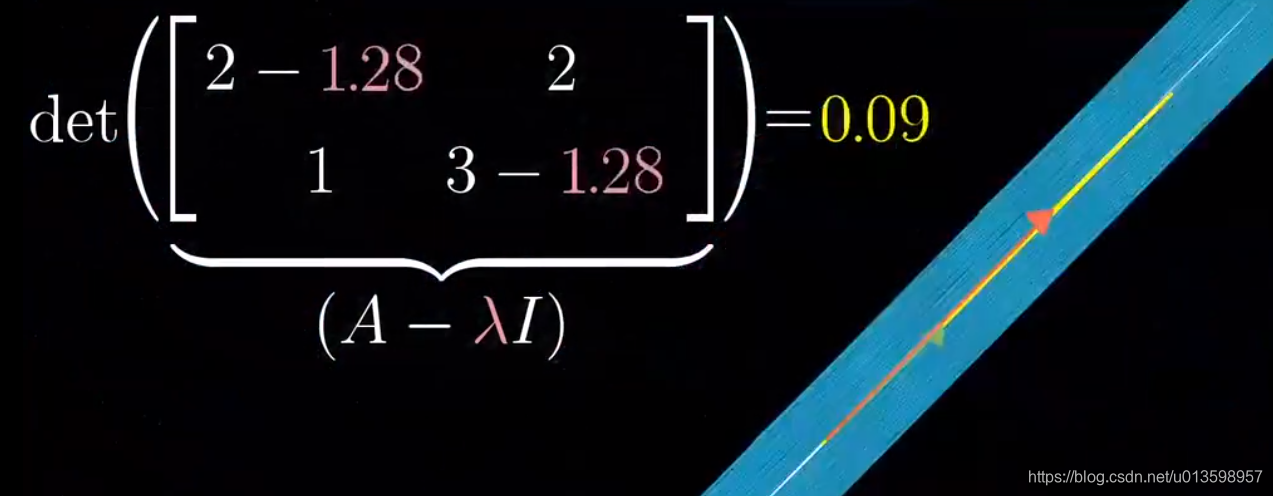
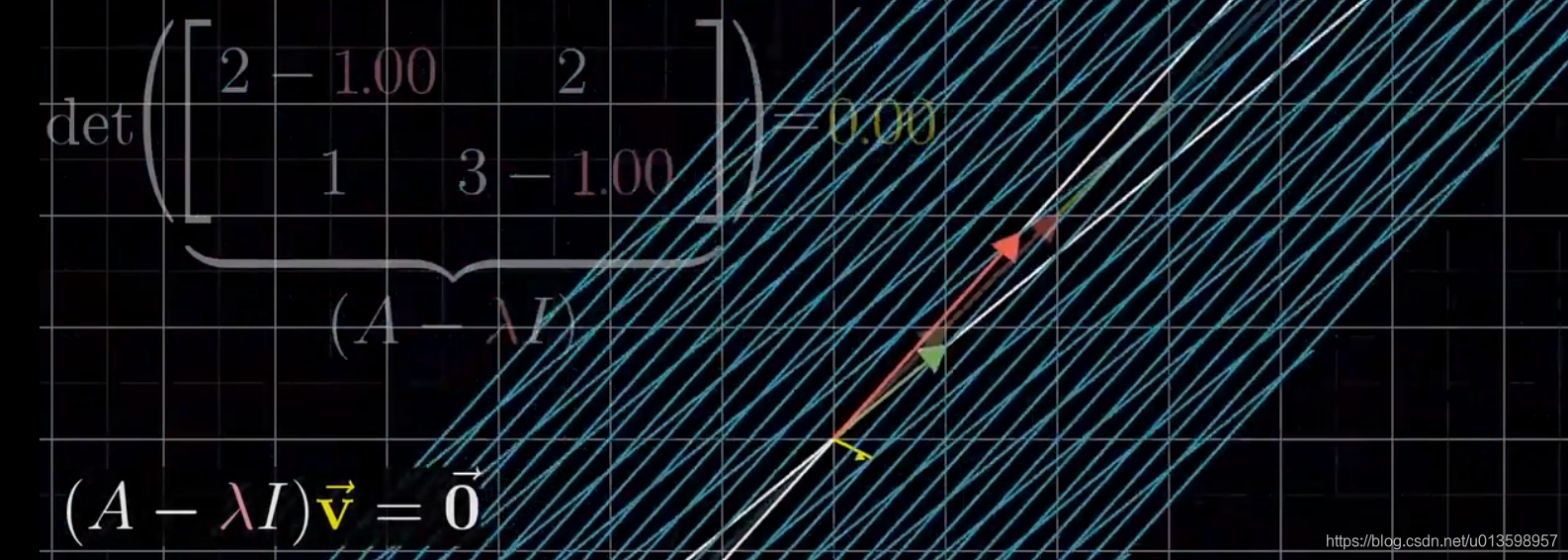
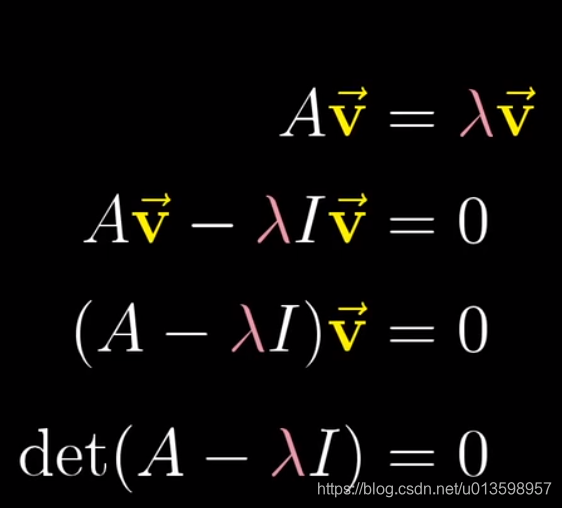
上图为运算转换思考。
下面回到开头的例子:
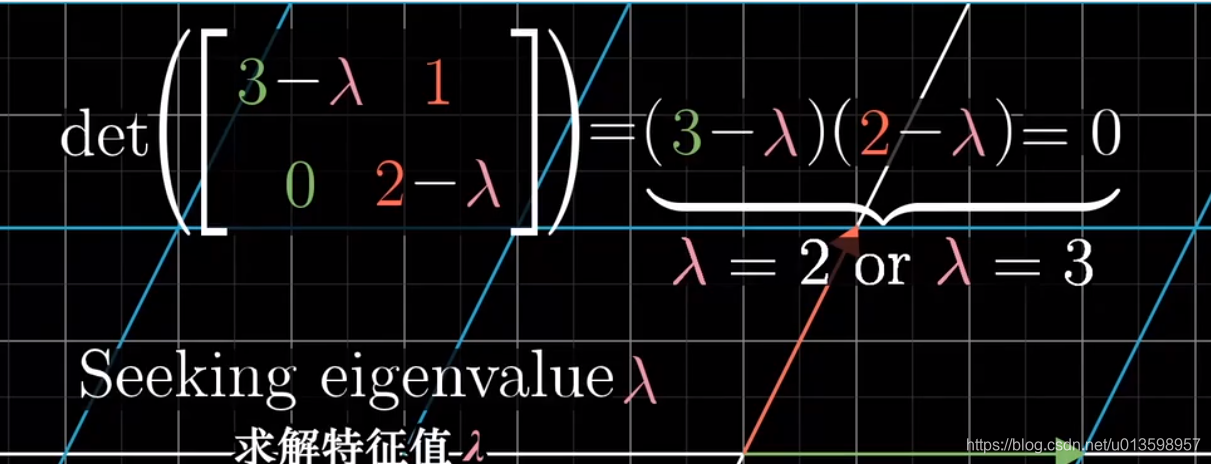
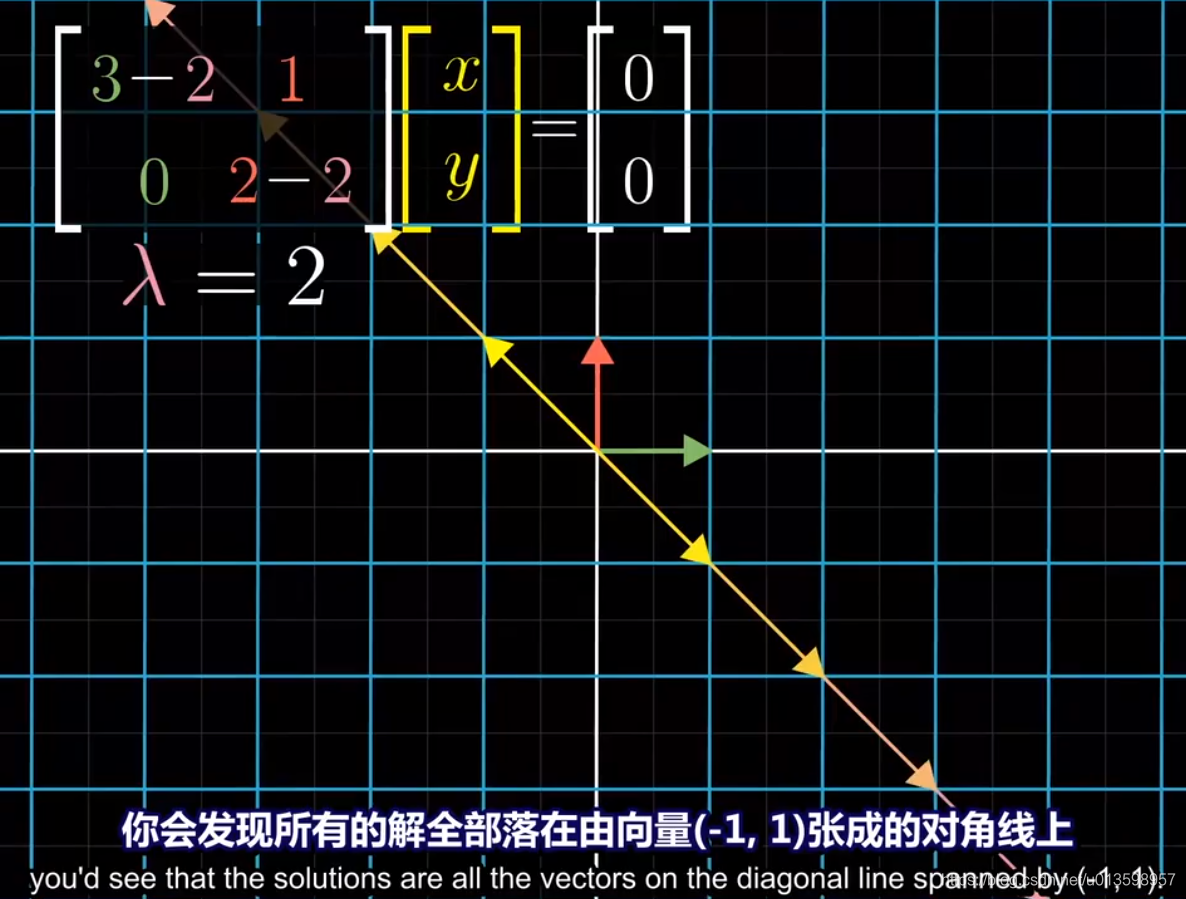
代入特征值2:
不过,二维变换不一定有特征向量。例子如下:

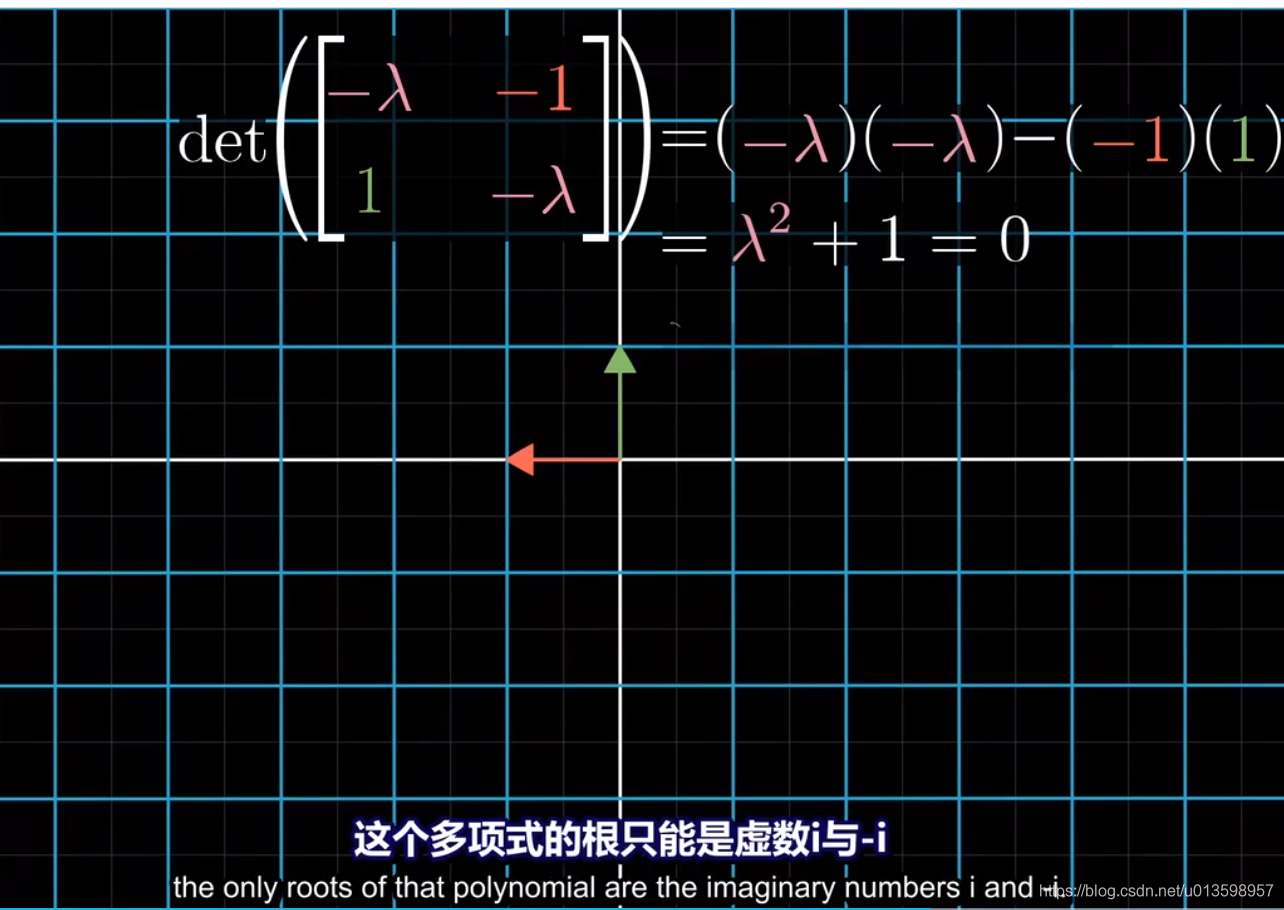
没有实数解表明它没有特征向量。
而对于二维的剪切变换:
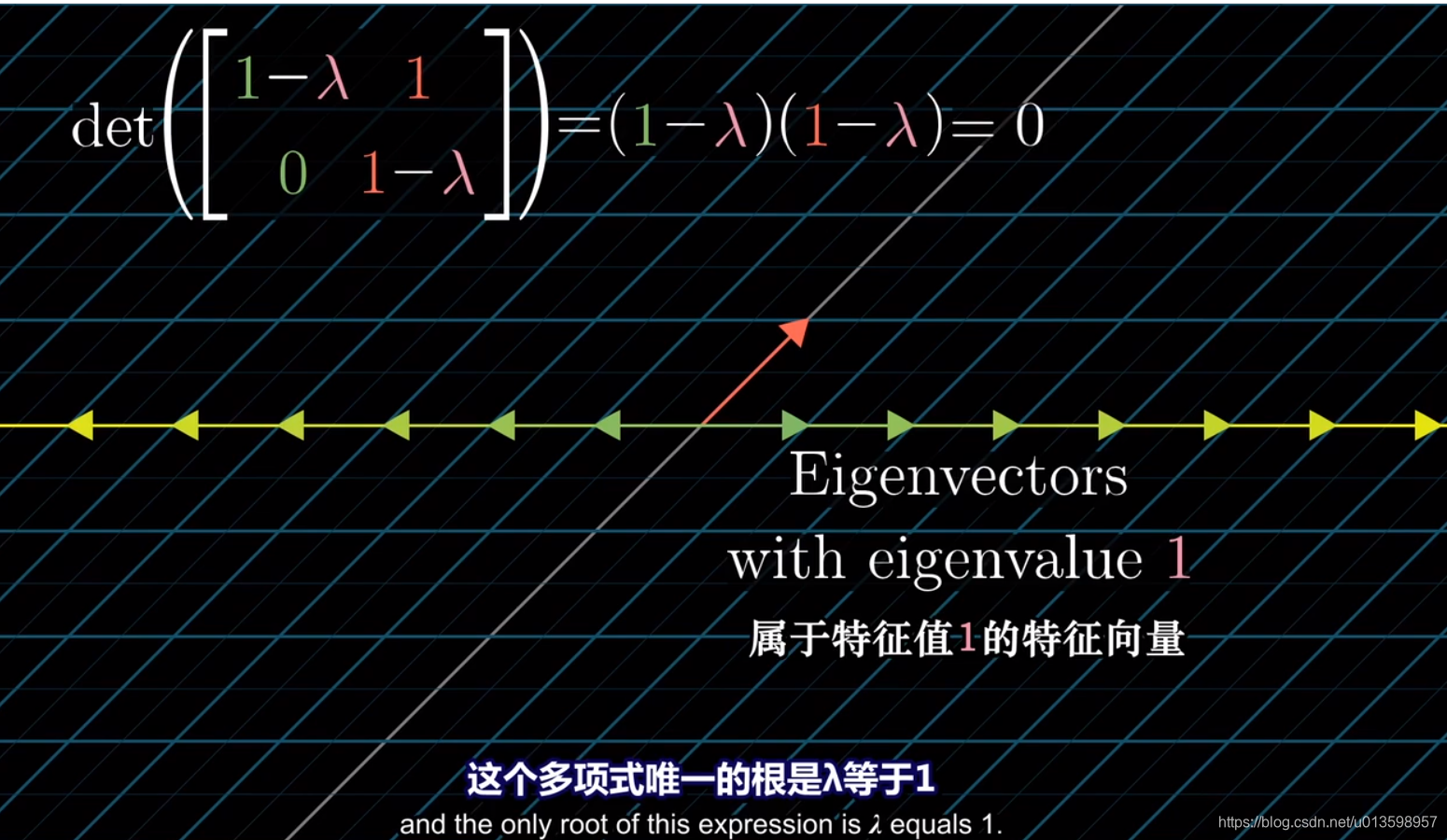
可能会出现只有一个特征值,但是特征向量不止在一条直线上的情况。下面引入特征基的概念。
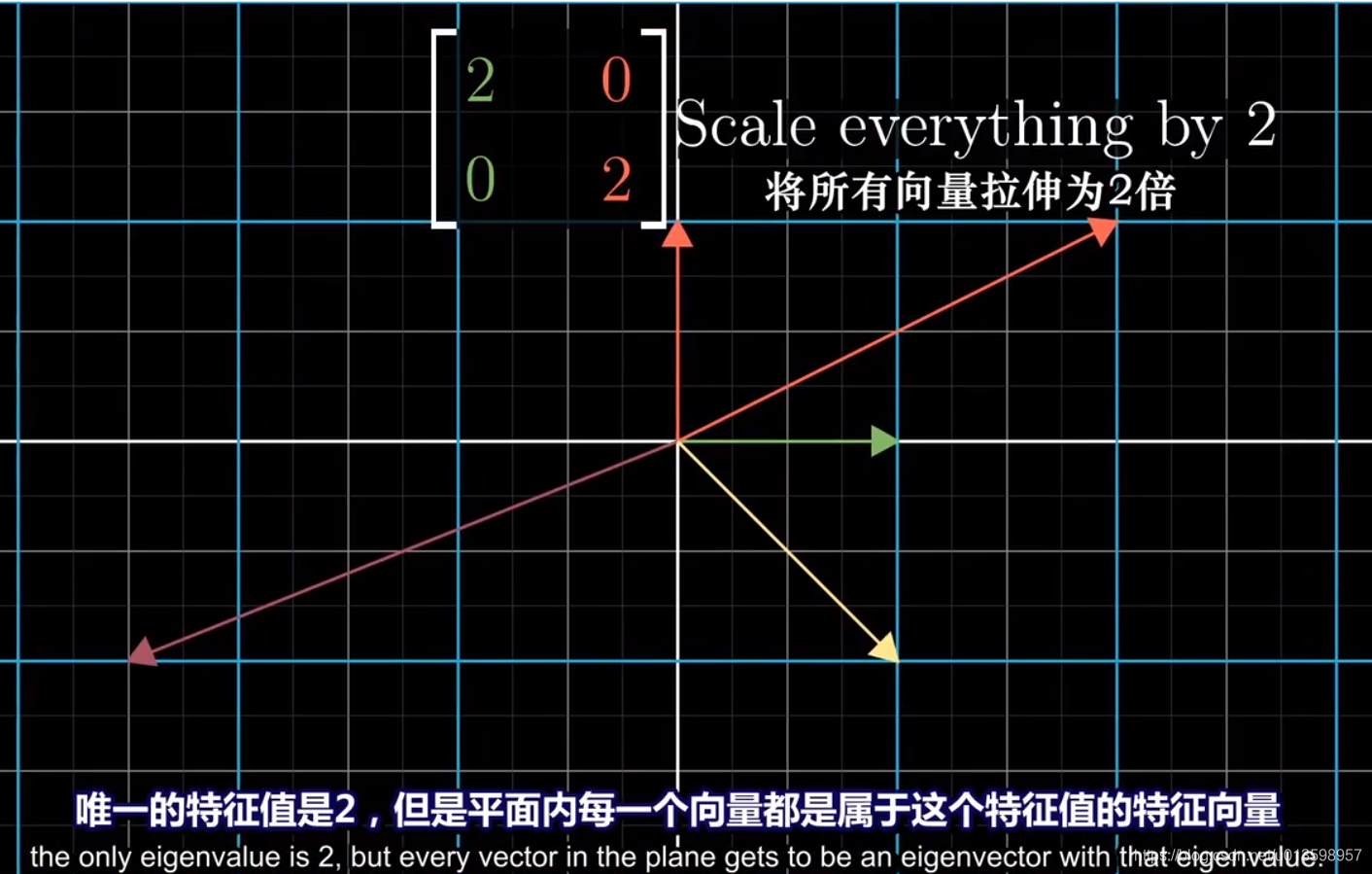
上图情景:如果基向量都是特征向量。

矩阵的对角元是这些基向量所属的特征值。
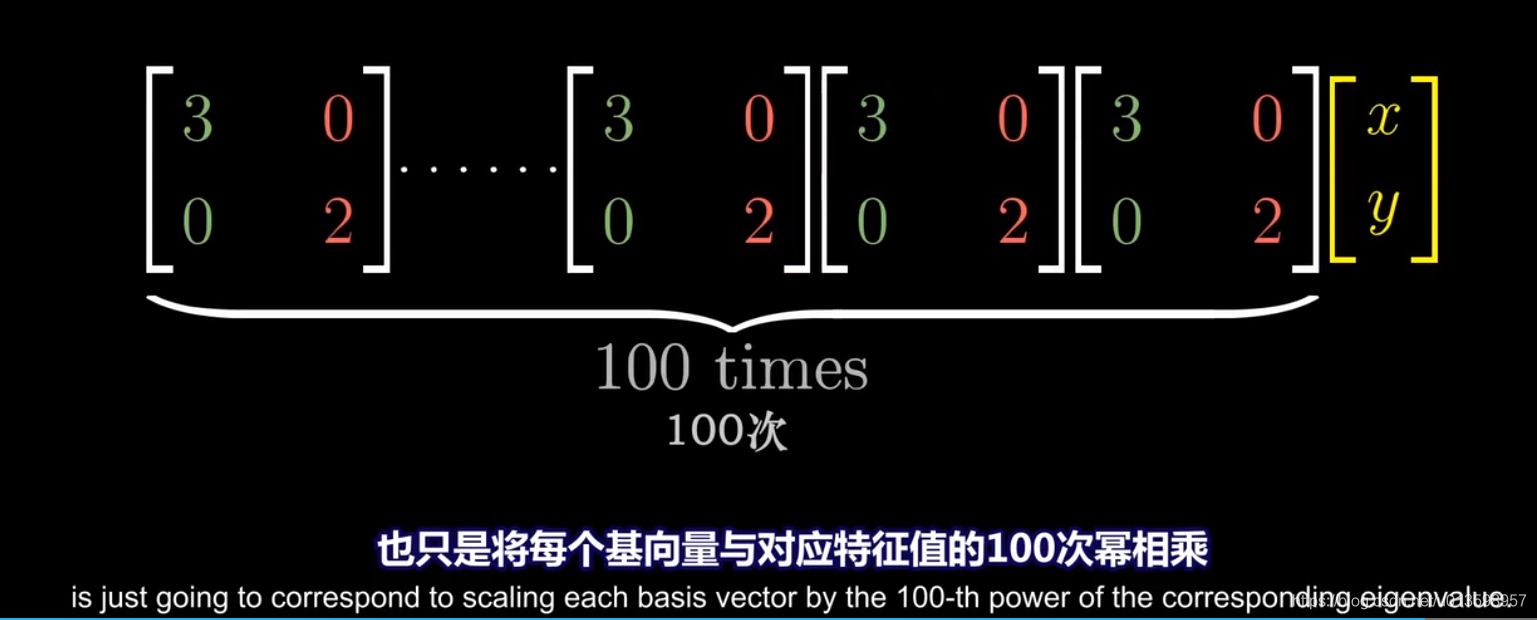
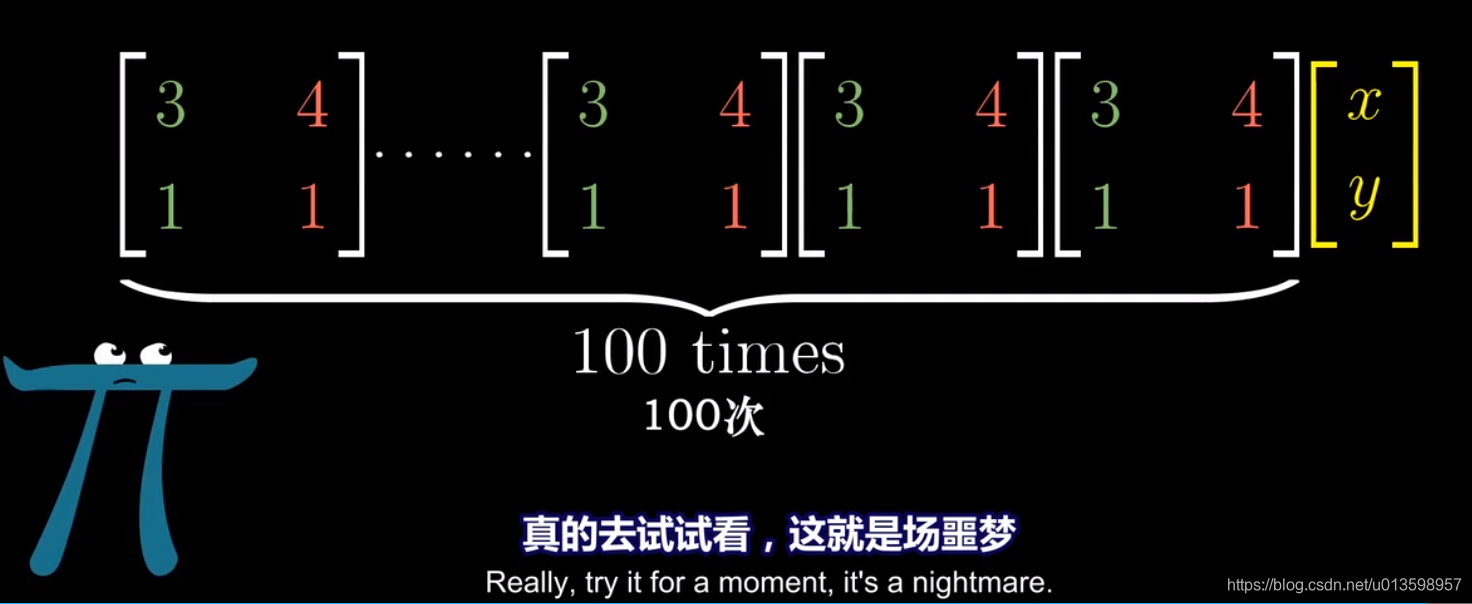
从上面两张图的对比更容易看出,对角矩阵在很多方面都更容易处理。对角矩阵仅仅让基向量与某个特征值相乘。
如果变换有许多特征向量,并满足:

使特征向量转换为新坐标系中的基向量,也能得到新坐标系下描述的变换:(可以说是对角化,为了简化运算)

特征基逆矩阵* 原描述变换 * 特征基矩阵,得到的新矩阵满足对角,是因为变换后(新描述角度下)所在坐标系的基向量,在变换过程中只进行了缩放。
前面提到,相比用矩阵(坐标系)描述线性变换,联系使用特征值和特征向量更方便,这个例子也印证了为什么。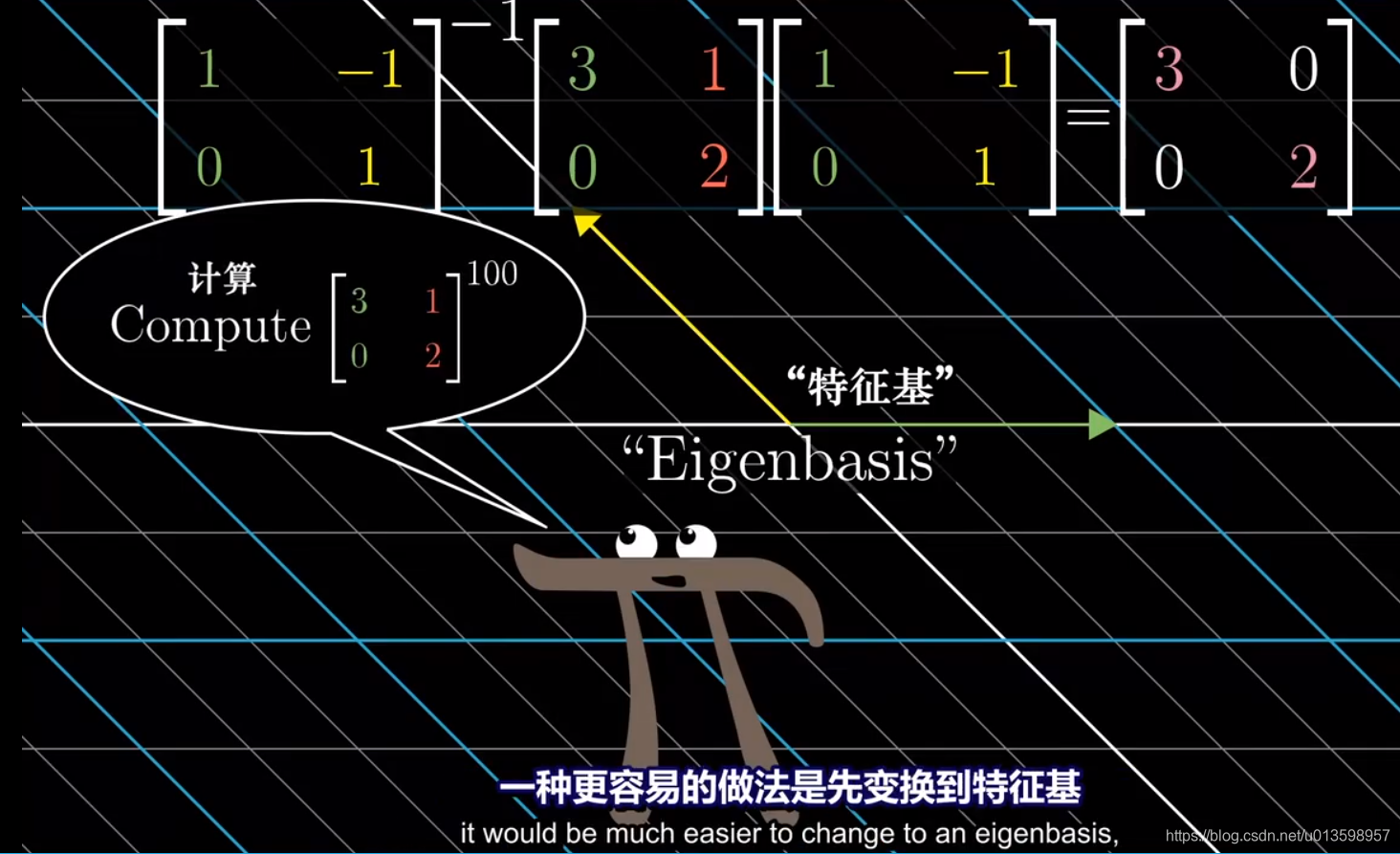
把原描述空间下的矩阵变换,转换为新描述空间下的变换。
但注意:

因此,如果能找到一组满足空间张成的特征基,那么线性变换运算将可以被简单化。
11 抽象向量空间
现在,让我们尝试坐标轴抛掉,去感受独立的空间。
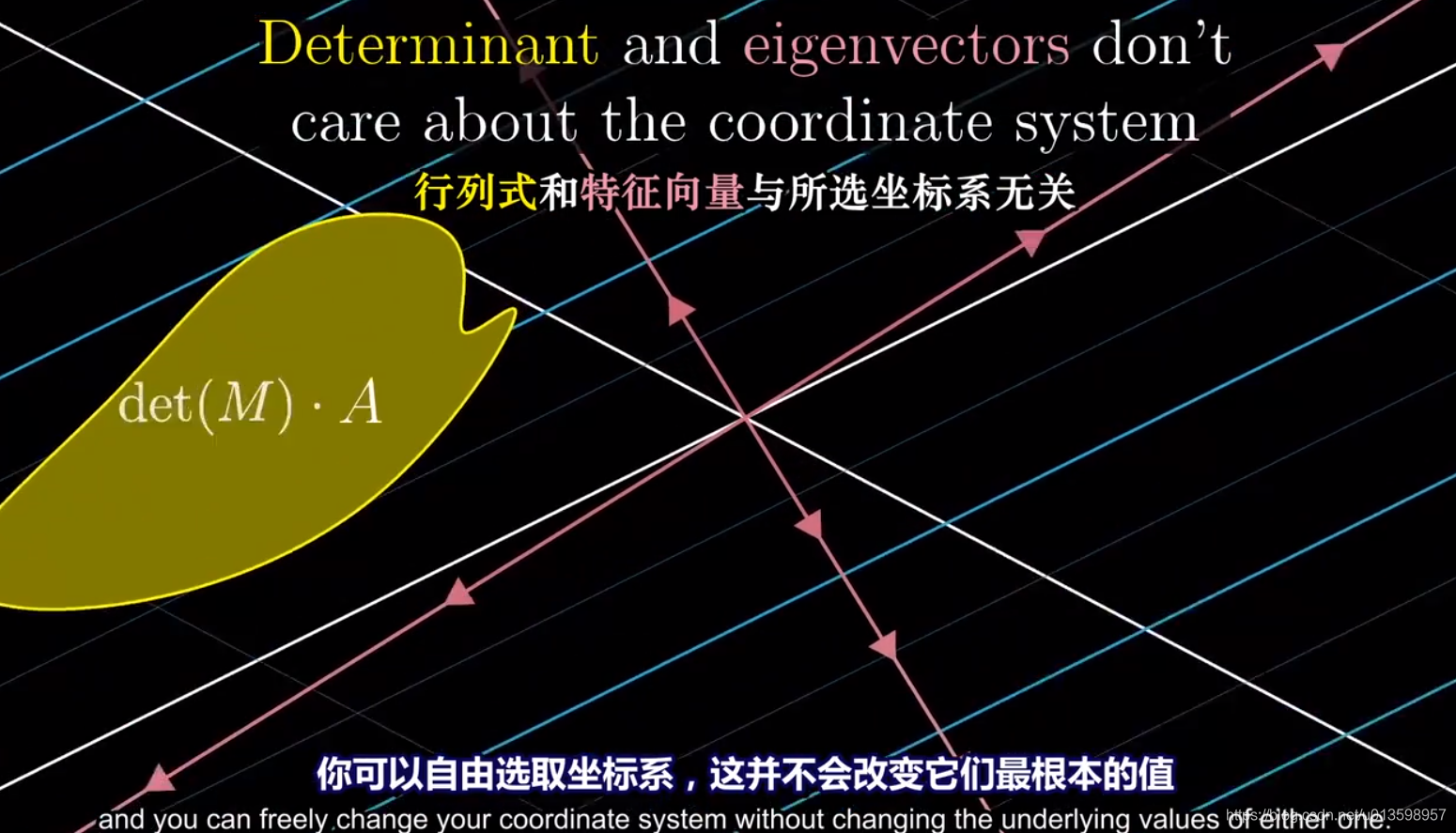
行列式代表一个变换对空间的缩放比例,特征向量则是在变换中停留在原来张成方向上的向量。这两者都是暗含于空间中的性质。
究竟怎么理解空间?
让我们谈论同样具有向量特性的存在——函数。
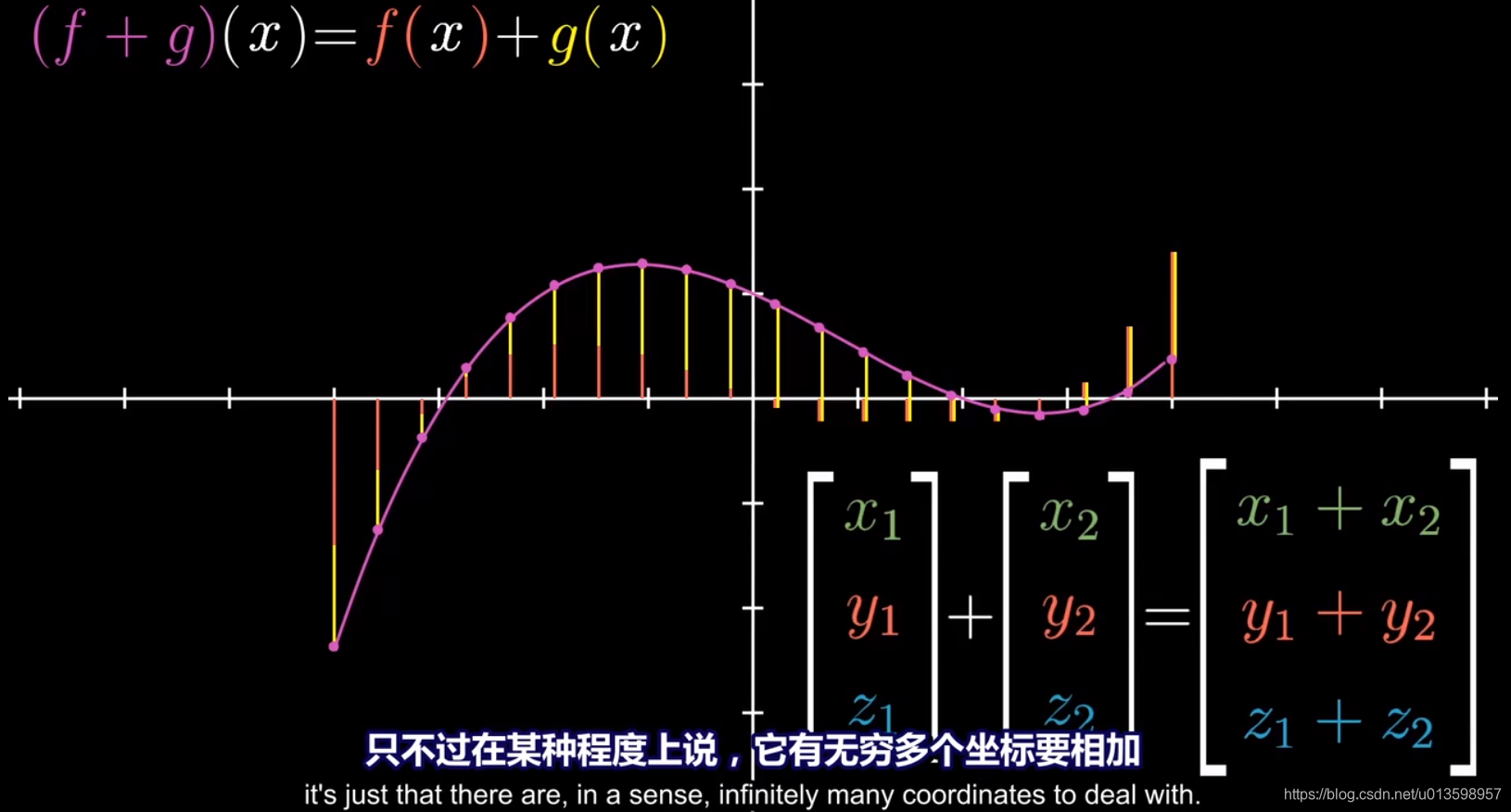
同样,还有数乘方面的类比。
线性代数的概念,可以被抽出用于函数。
相比第三课提到的线性(变换)的形象化定义,严格的定义更具抽象性:
在线性代数中,一个线性变换可以通过它对基向量的作用来完全描述。变换可被看成被线性分解为一小步。
在函数中,有求导可以分开求这样带有线性性质的例子。
让我们尝试用矩阵来描述求导:

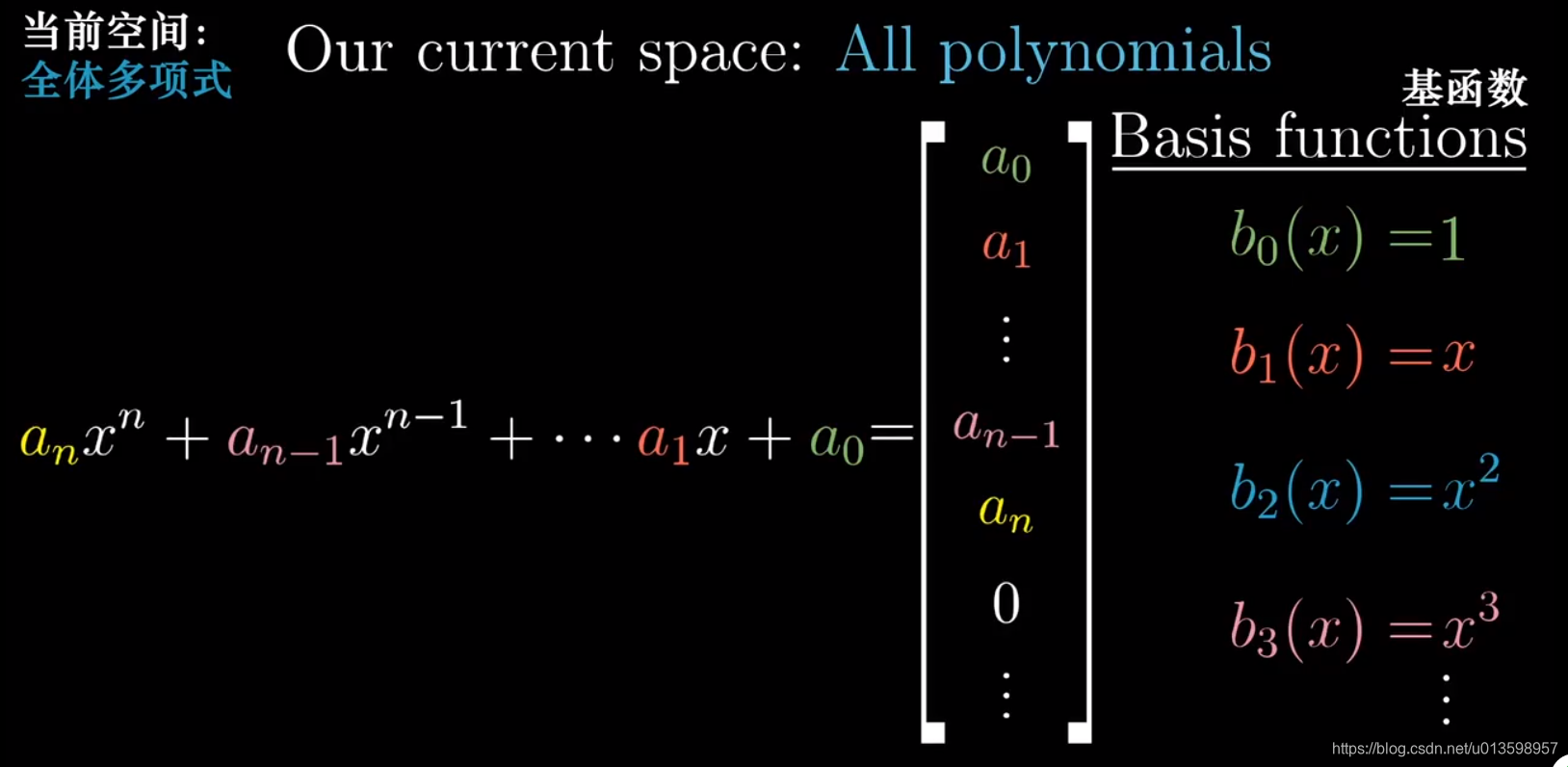
上图为无限阶矩阵。

上图,矩阵代表求导变换,常数1所在的维度变为零向量,x2所在的维度变换后伸长至原来的2倍。
推广:只要处理的对象集具有合理的数乘相加概念,线性代数中所有关于向量、线性变换和其他的概念应该适用于它。

在线性代数的现代理论中,如果想让所有已经建立好的理论和概念适用于一个向量空间,应满足八条公理。

本讲解聚焦于用几何图像、平行等距分布来介绍线性代数,但线性代数不止如此,它有更广泛的应用,其知识概念也存在于其他领域。
这也是为什么一些数学家/教科书倾向于以抽象的语言来定义讲解线性代数的知识。
所以,向量是什么?有很多种体现,或许没有具体 的答案,但是数学上可以把它抽象为“向量空间”这样一个无形的概念。