华中科技大学829自动控制原理真题分析系列博文是对华中科技大学829自动控制原理真题的详细剖析,详细讲解每一道题涉及的知识点、解题方法、不同的解答过程,即使是两道题涉及的知识点相似,我依然会将涉及到知识点写完整,原因是:考研的时间很宝贵,减少小伙伴往回翻知识点的时间;重复写知识点,小伙伴们反复看知识点,有利于小伙伴加强记忆,将知识点深深印在脑中。下面将为大家呈上几道剖析样题,大家有需要的话可以关注该系列博文,因为平时有工作,因此博文更新较慢,我争取尽快更新博文,当然,我会以高质量给大家更新博文。
- 典 型 二 阶 系 统 的 超 调 量 为 ( 典型二阶系统的超调量为( 典型二阶系统的超调量为( ) 。 )。 )。
A . e − π ξ 1 − ξ 2 A.e^{\frac{-\pi\xi}{\sqrt{1-\xi^2}}} A.e1−ξ2−πξ B . e ξ 1 − ξ 2 B.e^{\frac{\xi}{\sqrt{1-\xi^2}}} B.e1−ξ2ξ C . e ξ π 1 − ξ 2 C.e^{\frac{\xi}{\pi\sqrt{1-\xi^2}}} C.eπ1−ξ2ξ D . e π ξ 1 − ξ 2 D.e^{\frac{\pi\xi}{\sqrt{1-\xi^2}}} D.e1−ξ2πξ
解: 答 案 为 A 答案为A 答案为A。
相关知识点:
最 大 超 调 量 : σ % = c ( t p ) − c ( ∞ ) c ( ∞ ) = e − π ξ 1 − ξ 2 × 100 % ; 其 中 t p 为 峰 值 时 间 ; 上 升 时 间 : t r = π − β ω d = π − β ω n 1 − ξ 2 ; 峰 值 时 间 : t p = π ω d = π ω n 1 − ξ 2 ; 调 节 时 间 : t s = 3.5 ξ ω n = 3.5 σ , ( 误 差 带 : Δ = 0.05 ) ; t s = 4.4 ξ ω n = 4.4 σ , ( 误 差 带 : Δ = 0.02 ) ; \begin{aligned} &最大超调量:\sigma\%=\frac{c(t_p)-c(\infty)}{c(\infty)}=e^{-\frac{\pi\xi}{\sqrt{1-\xi^2}}}\times100\%;其中t_p为峰值时间;\\ &上升时间:t_r=\frac{\pi-\beta}{\omega_d}=\frac{\pi-\beta}{\omega_n\sqrt{1-\xi^2}};\\ &峰值时间:t_p=\frac{\pi}{\omega_d}=\frac{\pi}{\omega_n\sqrt{1-\xi^2}};\\ &调节时间:t_s=\frac{3.5}{\xi\omega_n}=\frac{3.5}{\sigma},(误差带:\Delta=0.05);t_s=\frac{4.4}{\xi\omega_n}=\frac{4.4}{\sigma},(误差带:\Delta=0.02); \end{aligned} 最大超调量:σ%=c(∞)c(tp)−c(∞)=e−1−ξ2πξ×100%;其中tp为峰值时间;上升时间:tr=ωdπ−β=ωn1−ξ2π−β;峰值时间:tp=ωdπ=ωn1−ξ2π;调节时间:ts=ξωn3.5=σ3.5,(误差带:Δ=0.05);ts=ξωn4.4=σ4.4,(误差带:Δ=0.02);
- 已 知 零 初 始 条 件 下 , 系 统 的 阶 跃 响 应 为 c ( t ) = 1 + 1 3 e − 4 t − 4 3 e − t , 求 系 统 的 传 递 函 数 。 已知零初始条件下,系统的阶跃响应为c(t)=1+\frac{1}{3}e^{-4t}-\frac{4}{3}e^{-t},求系统的传递函数。 已知零初始条件下,系统的阶跃响应为c(t)=1+31e−4t−34e−t,求系统的传递函数。
解:
输 出 响 应 的 拉 氏 变 换 : 输出响应的拉氏变换: 输出响应的拉氏变换:
C ( s ) = L [ c ( t ) ] = 1 s + 1 3 ⋅ 1 s + 4 − 4 3 ⋅ 1 s + 1 = 4 s ( s + 1 ) ( s + 4 ) C(s)=L[c(t)]=\frac{1}{s}+\frac{1}{3}·\frac{1}{s+4}-\frac{4}{3}·\frac{1}{s+1}=\frac{4}{s(s+1)(s+4)} C(s)=L[c(t)]=s1+31⋅s+41−34⋅s+11=s(s+1)(s+4)4
阶 跃 输 入 R ( s ) = 1 s , 因 此 , 系 统 的 传 递 函 数 为 : 阶跃输入R(s)=\frac{1}{s},因此,系统的传递函数为: 阶跃输入R(s)=s1,因此,系统的传递函数为:
C ( s ) R ( s ) = 4 ( s + 1 ) ( s + 4 ) \frac{C(s)}{R(s)}=\frac{4}{(s+1)(s+4)} R(s)C(s)=(s+1)(s+4)4
相关知识点:
(1) 典 型 输 入 : 典型输入: 典型输入:
(2) 常 用 的 拉 氏 变 换 : 常用的拉氏变换: 常用的拉氏变换:

解题框架:
a. 根 据 题 设 给 出 的 输 出 响 应 c ( t ) , 对 输 出 响 应 进 行 拉 氏 变 换 , 即 C ( s ) = L [ c ( t ) ] ; 根据题设给出的输出响应c(t),对输出响应进行拉氏变换,即C(s)=L[c(t)]; 根据题设给出的输出响应c(t),对输出响应进行拉氏变换,即C(s)=L[c(t)];
b. 根 据 题 设 给 出 的 输 入 r ( t ) , 对 输 入 进 行 拉 氏 变 换 , 即 R ( s ) = L [ r ( t ) ] ; 根据题设给出的输入r(t),对输入进行拉氏变换,即R(s)=L[r(t)]; 根据题设给出的输入r(t),对输入进行拉氏变换,即R(s)=L[r(t)];
c. 根 据 Φ ( s ) = C ( s ) R ( s ) , 求 得 传 递 函 数 。 根据\Phi(s)=\frac{C(s)}{R(s)},求得传递函数。 根据Φ(s)=R(s)C(s),求得传递函数。
- 已 知 已知 已知
G ( s ) = K ( s + 2 ) s 2 + 2 s + 2 G(s)=\frac{K(s+2)}{s^2+2s+2} G(s)=s2+2s+2K(s+2)
(1) 画 出 根 轨 迹 ; 画出根轨迹; 画出根轨迹;
(2) 问 K 取 何 值 时 , 系 统 处 于 过 阻 尼 和 欠 阻 尼 状 态 。 问K取何值时,系统处于过阻尼和欠阻尼状态。 问K取何值时,系统处于过阻尼和欠阻尼状态。
解:
(1)
① 分 支 数 、 起 止 点 。 因 n = 2 , m = 1 , n − m = 1 , 因 此 , 分 支 数 为 2 。 起 始 于 : p 1 = − 1 + j ; p 2 = − 1 − j ; 终 止 于 : z 1 = − 2 和 无 穷 远 处 ; 分支数、起止点。\\因n=2,m=1,n-m=1,因此,分支数为2。\\ 起始于:p_1=-1+j;p_2=-1-j;终止于:z_1=-2和无穷远处; 分支数、起止点。因n=2,m=1,n−m=1,因此,分支数为2。起始于:p1=−1+j;p2=−1−j;终止于:z1=−2和无穷远处;
② 在 实 轴 上 的 根 轨 迹 。 根 轨 迹 在 实 轴 上 的 范 围 为 : ( − ∞ , − 2 ] ; 在实轴上的根轨迹。\\根轨迹在实轴上的范围为:(-\infty,-2]; 在实轴上的根轨迹。根轨迹在实轴上的范围为:(−∞,−2];
③ 分 离 点 。 分 离 点 满 足 如 下 条 件 : 分离点。\\分离点满足如下条件: 分离点。分离点满足如下条件:
1 d + 1 + j + 1 d + 1 − j = 1 d + 2 \frac{1}{d+1+j}+\frac{1}{d+1-j}=\frac{1}{d+2} d+1+j1+d+1−j1=d+21
解 得 : d 1 = − 2 − 2 , d 2 = − 2 + 2 ( 舍 去 ) , 故 d = − 2 − 2 。 解得:d_1=-2-\sqrt{2},d_2=-2+\sqrt{2}(舍去),故d=-2-\sqrt{2}。 解得:d1=−2−2,d2=−2+2(舍去),故d=−2−2。
根 据 上 述 条 件 , 可 绘 制 根 轨 迹 如 下 : 根据上述条件,可绘制根轨迹如下: 根据上述条件,可绘制根轨迹如下:
(2)
由 模 值 条 件 可 知 , 根 轨 迹 与 实 轴 交 点 处 ( 交 点 为 ( − 2 − 2 , j 0 ) ) 的 K 1 值 : 由模值条件可知,根轨迹与实轴交点处(交点为(-2-\sqrt{2},j0))的K_1值: 由模值条件可知,根轨迹与实轴交点处(交点为(−2−2,j0))的K1值:
K 1 = ∣ ( − 2 − 2 ) − ( − 1 − j ) ∣ ⋅ ∣ ( − 2 − 2 ) − ( − 1 + j ) ∣ ∣ ( − 2 − 2 ) − ( − 2 ) ∣ = ∣ − 1 − 2 + j ∣ ⋅ ∣ − 1 − 2 − j ∣ ∣ − 2 ∣ = ( − 1 − 2 ) 2 + 1 2 ⋅ ( − 1 − 2 ) 2 + 1 2 ( 2 ) 2 = ( 1 + 2 ) 2 + 1 2 = 2 ( 2 + 1 ) \begin{aligned} K_1&=\frac{|(-2-\sqrt{2})-(-1-j)|·|(-2-\sqrt{2})-(-1+j)|}{|(-2-\sqrt{2})-(-2)|}\\ &=\frac{|-1-\sqrt{2}+j|·|-1-\sqrt{2}-j|}{|-\sqrt{2}|}\\ &=\frac{\sqrt{(-1-\sqrt2)^2+1^2}·\sqrt{(-1-\sqrt2)^2+1^2}}{(\sqrt{\sqrt{2}})^2}\\ &=\frac{(1+\sqrt{2})^2+1}{\sqrt{2}}\\ &=2(\sqrt{2}+1) \end{aligned} K1=∣(−2−2)−(−2)∣∣(−2−2)−(−1−j)∣⋅∣(−2−2)−(−1+j)∣=∣−2∣∣−1−2+j∣⋅∣−1−2−j∣=(2)2(−1−2)2+12⋅(−1−2)2+12=2(1+2)2+1=2(2+1)
因 此 , 当 0 < K < K 1 时 , 系 统 处 于 欠 阻 尼 状 态 ; 当 K = K 1 时 , 系 统 处 于 临 界 阻 尼 状 态 ; 当 K > K 1 时 , 系 统 处 于 过 阻 尼 状 态 。 因此,\\ 当0<K<K_1时,系统处于欠阻尼状态;\\ 当K=K_1时,系统处于临界阻尼状态;\\ 当K>K_1时,系统处于过阻尼状态。 因此,当0<K<K1时,系统处于欠阻尼状态;当K=K1时,系统处于临界阻尼状态;当K>K1时,系统处于过阻尼状态。
相关知识点:
(1) 常 规 根 轨 迹 绘 制 法 则 : 常规根轨迹绘制法则: 常规根轨迹绘制法则:
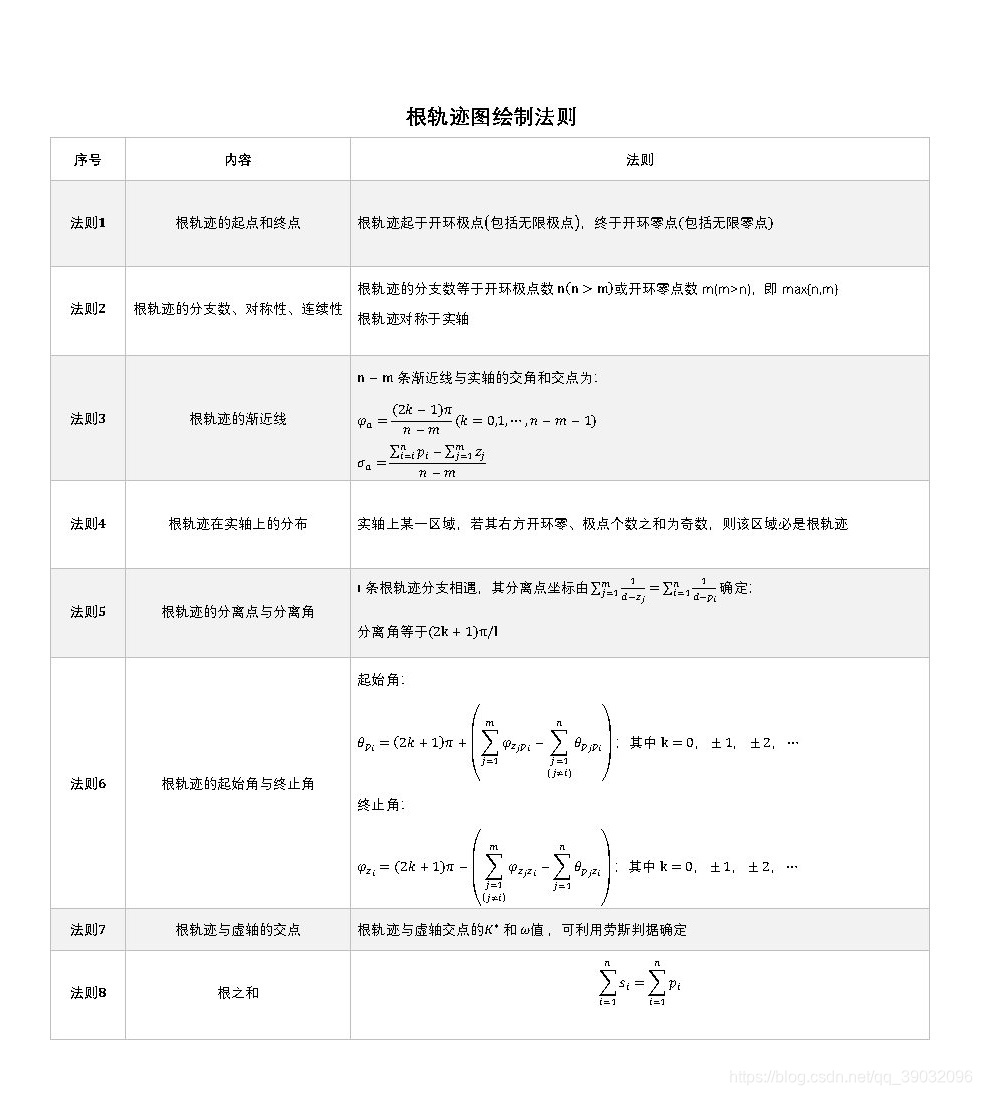
(2) 不 同 位 置 根 轨 迹 代 表 的 状 态 : 不同位置根轨迹代表的状态: 不同位置根轨迹代表的状态:
0 < K < K 1 时 , 系 统 处 于 过 阻 尼 状 态 , 系 统 单 位 阶 跃 响 应 无 超 调 , 呈 单 调 上 升 形 式 ; K = K 1 时 , 系 统 处 于 临 界 阻 尼 状 态 , 系 统 单 位 阶 跃 响 应 无 超 调 , 呈 单 调 上 升 形 式 ; K 1 < K < K 2 时 , 系 统 处 于 欠 阻 尼 状 态 , 系 统 单 位 阶 跃 响 应 有 超 调 , 呈 振 荡 形 式 ; K = K 2 时 , 系 统 处 于 无 阻 尼 状 态 , 系 统 单 位 阶 跃 响 应 临 界 稳 定 , 呈 等 幅 振 荡 形 式 ; K > K 2 时 , 系 统 单 位 阶 跃 响 应 不 稳 定 , 呈 发 散 形 式 。 \begin{aligned} &0<K<K_1时,系统处于过阻尼状态,系统单位阶跃响应无超调,呈单调上升形式;\\ &K=K_1时,系统处于临界阻尼状态,系统单位阶跃响应无超调,呈单调上升形式;\\ &K_1<K<K_2时,系统处于欠阻尼状态,系统单位阶跃响应有超调,呈振荡形式;\\ &K=K_2时,系统处于无阻尼状态,系统单位阶跃响应临界稳定,呈等幅振荡形式;\\ &K>K_2时,系统单位阶跃响应不稳定,呈发散形式。 \end{aligned} 0<K<K1时,系统处于过阻尼状态,系统单位阶跃响应无超调,呈单调上升形式;K=K1时,系统处于临界阻尼状态,系统单位阶跃响应无超调,呈单调上升形式;K1<K<K2时,系统处于欠阻尼状态,系统单位阶跃响应有超调,呈振荡形式;K=K2时,系统处于无阻尼状态,系统单位阶跃响应临界稳定,呈等幅振荡形式;K>K2时,系统单位阶跃响应不稳定,呈发散形式。
(3) 相 角 条 件 和 模 值 条 件 : 相角条件和模值条件: 相角条件和模值条件:
根 轨 迹 可 以 由 如 下 两 个 方 程 描 述 , 第 一 个 方 程 称 为 相 角 条 件 , 第 二 个 方 程 称 为 模 值 条 件 。 根轨迹可以由如下两个方程描述,第一个方程称为相角条件,第二个方程称为模值条件。 根轨迹可以由如下两个方程描述,第一个方程称为相角条件,第二个方程称为模值条件。
∑ j = 1 m ∠ ( s − z j ) − ∑ i = 1 n ∠ ( s − p i ) = ( 2 k + 1 ) π ( k = 0 , ± 1 , ± 2 , … ) \sum_{j=1}^m \angle(s-z_j)-\sum_{i=1}^n \angle(s-p_i)=(2k+1)\pi(k=0,±1,±2,\dots) j=1∑m∠(s−zj)−i=1∑n∠(s−pi)=(2k+1)π(k=0,±1,±2,…)
K ∗ = ∏ i = 1 n ∣ s − p i ∣ ∏ j = 1 m ∣ s − z j ∣ K^*=\frac{\prod_{i=1}^n |s-p_i|}{\prod_{j=1}^m |s-z_j|} K∗=∏j=1m∣s−zj∣∏i=1n∣s−pi∣
其 中 : 相 角 条 件 是 确 定 s 平 面 上 根 轨 迹 的 充 分 必 要 条 件 , 模 值 条 件 用 于 确 定 根 轨 迹 上 各 点 的 K ∗ 值 。 其中:相角条件是确定s平面上根轨迹的充分必要条件,模值条件用于确定根轨迹上各点的K^*值。 其中:相角条件是确定s平面上根轨迹的充分必要条件,模值条件用于确定根轨迹上各点的K∗值。
解题框架:
a. 根 据 题 设 给 出 的 开 环 传 递 函 数 , 化 为 根 轨 迹 标 准 形 式 ( 首 Ⅰ 型 ) ; 根据题设给出的开环传递函数,化为根轨迹标准形式(首Ⅰ型); 根据题设给出的开环传递函数,化为根轨迹标准形式(首Ⅰ型);
K ∗ ∏ j = 1 m ( s − z j ) ∏ i = 1 n ( s − p i ) K^*\frac{\prod_{j=1}^m (s-z_j)}{\prod_{i=1}^n (s-p_i)} K∗∏i=1n(s−pi)∏j=1m(s−zj)
b. 根 据 特 征 方 程 : D ( s ) = 1 + G ( s ) H ( s ) = 0 , 判 断 所 求 根 轨 迹 类 型 ( 180 ° 根 轨 迹 、 0 ° 根 轨 迹 、 参 数 根 轨 迹 ) ; 根据特征方程:D(s)=1+G(s)H(s)=0,判断所求根轨迹类型(180°根轨迹、0°根轨迹、参数根轨迹); 根据特征方程:D(s)=1+G(s)H(s)=0,判断所求根轨迹类型(180°根轨迹、0°根轨迹、参数根轨迹);
c. 根 据 根 轨 迹 绘 制 法 则 , 绘 制 根 轨 迹 ; 根据根轨迹绘制法则,绘制根轨迹; 根据根轨迹绘制法则,绘制根轨迹;
c.1 根轨迹绘制常用步骤(考试重点):
① 分 支 数 、 起 止 点 。 因 n = ~ , m = ~ , n − m = ~ , 因 此 , 分 支 数 为 ~ 。 起 始 于 ( 极 点 ) : p 1 = ~ ; p 2 = ~ ; 终 止 于 ( 零 点 ) : z 1 = ~ 和 无 穷 远 处 ; 分支数、起止点。\\ 因n=~,m=~,n-m=~,因此,分支数为~。\\ 起始于(极点):p_1=~;p_2=~;终止于(零点):z_1=~和无穷远处; 分支数、起止点。因n=~,m=~,n−m=~,因此,分支数为~。起始于(极点):p1=~;p2=~;终止于(零点):z1=~和无穷远处;
② 在 实 轴 上 的 根 轨 迹 。 根 轨 迹 在 实 轴 上 的 范 围 为 : ~ ; 在实轴上的根轨迹。\\ 根轨迹在实轴上的范围为:~; 在实轴上的根轨迹。根轨迹在实轴上的范围为:~;
③ 渐 近 线 。 渐 近 线 满 足 如 下 条 件 : 渐近线。\\ 渐近线满足如下条件: 渐近线。渐近线满足如下条件:
渐 近 线 与 实 轴 交 点 : σ a = ∑ i = 1 n p i − ∑ j = 1 m z j n − m 渐 近 线 与 实 轴 夹 角 : ϕ a = ( 2 k + 1 ) π n − m ( k = 0 , 1 , … … , n − m − 1 ) \begin{aligned} &渐近线与实轴交点:\sigma_a=\frac{\sum_{i=1}^n{p_i}-\sum_{j=1}^m{z_j}}{n-m}\\ &渐近线与实轴夹角:\phi_a=\frac{(2k+1)\pi}{n-m}(k=0,1,……,n-m-1) \end{aligned} 渐近线与实轴交点:σa=n−m∑i=1npi−∑j=1mzj渐近线与实轴夹角:ϕa=n−m(2k+1)π(k=0,1,……,n−m−1)
④ 分 离 点 。 分 离 点 满 足 如 下 条 件 : 分离点。\\ 分离点满足如下条件: 分离点。分离点满足如下条件:
分 离 点 : ∑ j = 1 m 1 d − z j = ∑ i = 1 n 1 d − p i ; 分 离 角 : ( 2 k + 1 ) π l \begin{aligned} &分离点:\sum_{j=1}^m{\frac{1}{d-z_j}}=\sum_{i=1}^n{\frac{1}{d-p_i}};\\ &分离角:\frac{(2k+1)\pi}{l} \end{aligned} 分离点:j=1∑md−zj1=i=1∑nd−pi1;分离角:l(2k+1)π
d. 根 据 根 轨 迹 进 行 定 量 定 性 分 析 。 根据根轨迹进行定量定性分析。 根据根轨迹进行定量定性分析。
注:根轨迹绘制法则可参考链接: 自动控制–控制系统根轨迹篇.在控制系统根轨迹篇详细介绍了180°根轨迹和0°根轨迹的绘制法则,并且具有例题进行说明。
接下来的829系列博客将采用以上风格来更新,如果觉得对自己考研复习有帮助的小伙伴可以继续学习该系列博客。(当然,会收取一定的费用,但是不会很高。)


