小算法

1、快速幂和矩阵快速幂

快速幂

ll poww(ll a,ll k)
{
    
    
    ll ans=1;
    while(k>1)
    {
    
    
        if(k%2==1)ans*=a;
        a*a;
        k>>1;
    }
    return ans*a;
}

矩阵快速幂

矩阵乘法

void mul(ll a[][maxn],ll b[][maxn],ll n)
{
    
    
    ll temp[maxn][maxn];
    rep(i,1,n)
    rep(j,1,n)temp[i][j]=0;

    rep(i,1,n)
    rep(j,1,n)
    rep(k,1,n)
    {
    
    
        temp[i][j]+=a[i][k]*b[k][j];
        temp[i][j]%=MOD;
    }
    rep(i,1,n)
    rep(j,1,n)a[i][j]=temp[i][j];
}

矩阵快速幂

void pow(ll a[][maxn],ll n,ll k)
{
    
    
    ll temp[maxn][maxn];
    rep(i,1,n)
    rep(j,1,n)
    {
    
    
        if(i==j)temp[i][j]=1;
        else temp[i][j]=0;
    }
    while(k>1)
    {
    
    
        if(k%2==1)mul(temp,a,n);
        mul(a,a,n);
        k/=2;
    }
    mul(a,temp,n);

2、离散化

引入

color the ball
这是我们都做过的例题color the ball,就是一个简单的差分数组。
但是如果我们把n拓展到1e19，最后的询问改成查询第i个气球。
朴素的差分数组就显得力不从心了，因为根本就打不出1e19的数组。我们需要离散化来节约空间。

定义

离散化：把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

我们有时候开了一个1e7甚至1e8的数组来维护数据结构，但是实际用到的点只有1e4或者1e5，中间的很多空间就浪费了。就像上面这张图，我们只需要维护和五个点有关的区间修改，如果去打1e19的数组就显得很离谱。

具体实现

实际上离散化的算法实现是非常简单的。
1、我们先离线所有的输入和询问。

2、我们把所有用到的数据进行排序。
3、把原来的数据和离线化后的数据进行映射。

那么原来修改【10064，144968】就变成了修改新区间【5，6】，一学就会。

代码参考

这边用简单的区间修改为例，输入输入为n组区间修改，格式为【l,r】（l<r）

    ll l[100000],r[100000];
    vector<ll>v;用这个vector来离线存储所有数据
    for(int i=1;i<=n;i++)
    {
    
    
        scanf("%lld%lld",&l[i],&r[i]);
        v.push_back(l[i]);
        v.push_back(r[i]);
    }
    sort(v.begin(),v.end());排序
    v.erase(unique(v.begin(),v.end()),v.end());
    unique是用来去重的函数，返回值是去重后一个元素的地址。
    for(int i=1;i<=n;i++)
    {
    
    
        l[i]=lower_bound(v.begin(),v.end(),l[i])-v.begin()+1;
        这个时候新的l[i]的值就是对应的l[i]在vector中的下标
        r[i]=lower_bound(v.begin(),v.end(),r[i])-v.begin()+1;
        printf("%lld %lld\n",l[i],r[i]);
    }

测试数据

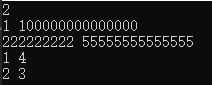
可以看到，这个有很多0的数就被映射成了4

进阶

当然，上面这种映射方式还有缺陷，当我们要修改形如[l,l]（即l==r）的时候，在上述的映射方式中找不到一个区间去修改，就很懵逼。
解决方式也是简单的。我们在每个数后面插入一个（虽然这样会使空间变成原来的两倍，但是相比于离散化所节约的空间来讲还是不值一提），然后修改一下区间的命名规则。

这样就把修改单点转化成了原来的区间修改。

在线段树中的应用

我在用离散化后的数据写线段树的时候被一些小细节折磨的很惨，在这边写一下用离散化写线段树需要注意的细节。

建树

void build(ll p,ll l,ll r)
{
    
    

    tree[p]=0;
    laz[p]=0;
    if(l+1==r)return ;
	首先，叶子节点性质发现了变化，原先我们的命名规则是左右的闭区间，当左节点等于右节点的时候return
	而现在我们的命名规则是左闭右开区间，所以当左节点+1等于右节点的时候return
    ll mid=l+r>>1;
    build(p>>1,l,mid);
    build(p>>1|1,mid,r);
    原先我们的左子树所掌管的区间是l到mid（左闭有闭区间），所以右区间掌管的区间为mid+1到r，否则就重复了
    而现在我们的命名规则改了，左子树是l到mid（左闭右开），所以右区间就变成mid到r（左闭右开），有人会问那r+1
    谁来维护呢？没必要维护，因为这个点是我们创造出来的，实际询问的时候没有这个点。具体见上面“进阶”
}

修改

void update(ll p,ll l,ll r,ll x,ll y,ll w)
{
    
    
    if(l>=x&&r<=y)
    {
    
    
      
        return ;
    }
    if(l+1==r)return;这边不加这个会死循环，道理和二分是一样的
    pushdown(p,l,r);
    ll mid=ms;
    if(x<mid)update(ls,l,mid,x,y,w);
    if(y>mid)update(rs,mid,r,x,y,w);这边如果改成y>=mid会出现问题（留给读者思考）
    cover[p]=cover[ls]&cover[rs];
}

查询也就没啥更多需要注意的细节了。

给出一道例题：
Mayor’s posters
参考代码：

#include<iostream>
#include<stdio.h>
#include<vector>
#include<math.h>
#include<algorithm>
#define ll long long
#define pb push_back
#define ls p<<1
#define rs p<<1|1
#define ms l+r>>1

const int maxn=8e5+5;
using namespace std;
ll tree[maxn],laz[maxn],a[maxn],cover[maxn];


void build(ll p,ll l,ll r)
{
    
    
//    printf("%lld %lld %lld\n",p,l,r);
    tree[p]=0;
    laz[p]=0;
    cover[p]=0;
    if(l+1==r)return ;

    ll mid=ms;
    build(ls,l,mid);
    build(rs,mid,r);
}
void pushdown(ll p,ll l,ll r)
{
    
    
    if(laz[p]!=0)
    {
    
    
        cover[ls]=1;
        cover[rs]=1;
        laz[ls]=laz[p];
        laz[rs]=laz[p];
        laz[p]=0;
    }
}
void update(ll p,ll l,ll r,ll x,ll y,ll w)
{
    
    
//    printf("%lld %lld %lld %lld %lld %lld\n",p,l,r,x,y,w);
    if(l>=x&&r<=y)
    {
    
    
        cover[p]=1;
        laz[p]=1;
        return ;
    }
    if(l+1==r)return;
    pushdown(p,l,r);
    ll mid=ms;
    if(x<mid)update(ls,l,mid,x,y,w);
    if(y>=mid)update(rs,mid,r,x,y,w);
    cover[p]=cover[ls]&cover[rs];
}


ll query(ll p,ll l,ll r,ll x,ll y)
{
    
    
//   printf("%lld %lld %lld %lld %lld\n",p,l,r,x,y);
    if(l>=x&&r<=y)return cover[p];
    pushdown(p,l,r);
    ll mid=ms,ans=1;
    if(x<mid)ans&=query(ls,l,mid,x,y);
    if(y>mid)ans&=query(rs,mid,r,x,y);

    return ans;
}
ll l[maxn],r[maxn],sub[maxn],real[maxn];
vector<ll>v;
int main()
{
    
    
    int c;
    scanf("%d",&c);
    while(c--)
    {
    
    
        int n;
        scanf("%d",&n);
        n=n+1;
        n=n-1;
        v.clear();


        int cnt=0;
        for(int i=1;i<=n;i++)
        {
    
    
            scanf("%d%d",&l[i],&r[i]);
            v.pb(l[i]);
            v.pb(l[i]+1);
            v.pb(r[i]);
            v.pb(r[i]+1);
        }
        sort(v.begin(),v.end());
        v.erase(unique(v.begin(),v.end()),v.end());
        build(1,1,v.size());
        for(int i=1;i<=n;i++)
        {
    
    
            l[i]=lower_bound(v.begin(),v.end(),l[i])-v.begin()+1;
            r[i]=lower_bound(v.begin(),v.end(),r[i])-v.begin()+1;
        }

        for(int i=n;i>=1;i--)
        {
    
    
            if(query(1,1,v.size(),l[i],r[i]+1)==0)cnt++;
            update(1,1,v.size(),l[i],r[i]+1,1);
        }
        cout<<cnt<<endl;


    }

}

3、二分求最大平均值

Max Median
题意：给出一个长度为n的序列，求其中长度大于k的连续段的最大中位数。

二分一个中位数，然后吧所有大于这个数的值标记为1，小于这个数的标记为0。
问题转变为求解方程 $S[l]-S[r]<(l-r)/2$ 是否有解。
注意到方程可以变形为 $2\ast S[l]-l<2\ast S[r]-r$ 问题就迎刃而解了。