Sklearn官方文档中文整理2——监督学习之线性和二次判别分析篇

1. 监督学习

1.2. 线性和二次判别分析【discriminant_analysis.LinearDiscriminantAnalysis和discriminant_analysis.QuadraticDiscriminantAnalysis】

Linear Discriminant Analysis（线性判别分析）(discriminant_analysis.LinearDiscriminantAnalysis) 和 Quadratic Discriminant Analysis （二次判别分析）(discriminant_analysis.QuadraticDiscriminantAnalysis) 是两个经典的分类器。 正如他们名字所描述的那样，他们分别代表了线性决策平面和二次决策平面。

这些分类器十分具有吸引力，因为他们可以很容易计算得到闭式解(即解析解)，其天生具有多分类的特性，在实践中已经被证明很有效，并且无需调参。

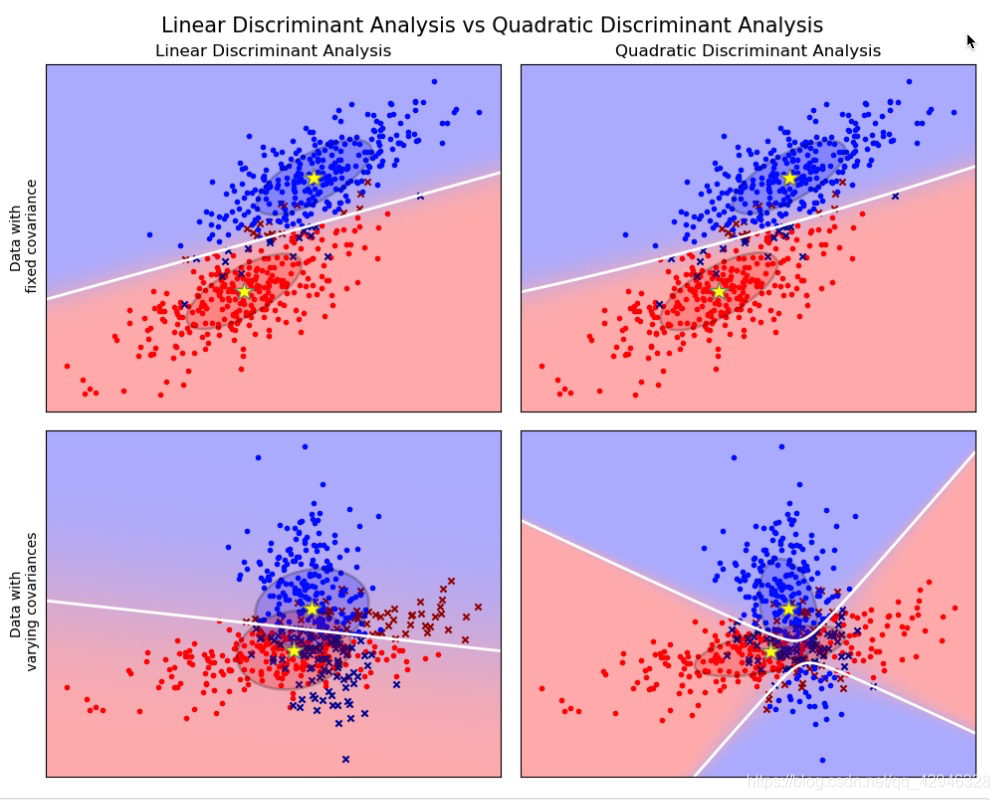
以上这些图像展示了 Linear Discriminant Analysis （线性判别分析）以及 Quadratic Discriminant Analysis （二次判别分析）的决策边界。其中，最后一行表明了线性判别分析只能学习线性边界， 而二次判别分析则可以学习二次边界，因此它相对而言更加灵活。

sklearn.discriminant_analysis.LinearDiscriminantAnalysis

参数	解释
solver:{‘svd’, ‘lsqr’, ‘eigen’}, default=’svd’	要使用的解算器，可能值：‘svd’: 奇异值分解（默认）。不计算协方差矩阵，因此建议对具有大量特征的数据使用此解算器。‘lsqr’:最小二乘解。可与收缩或自定义协方差估计相结合。‘eigen’: 特征值分解。可与收缩或自定义协方差估计相结合。
shrinkage：‘auto’ or float, default=None	收缩参数，可能值：None: 没有收缩（默认）。‘auto’: 用Ledoit-Wolf引理自动收缩。float between 0 and 1:固定收缩参数。如果使用协方差估计器，则应将其保留为“None”。请注意，收缩仅适用于“lsqr”和“eigen”解算器。
priors：array-like of shape (n_classes,), default=None	类先验概率。默认情况下，类比例是从训练数据中推断出来的。
n_components：int, default=None	用于降维的组件数量(<= min(n_classes - 1, n_features)) 。如果没有，将设置为min(n_classes - 1, n_features)。此参数仅影响变换方法。
store_covariance：bool, default=False	如果为True，则当解算器为“svd”时，明确计算类内加权协方差矩阵。矩阵总是为其他解算器计算和存储的。
tol：float, default=1.0e-4	将X的奇异值视为有效的绝对阈值，用于估计X的秩。将丢弃奇异值为非有效的维数。仅当解算器为“svd”时使用。
covariance_estimator：covariance estimator, default=None	如果不是None，则使用covariance_estimator来估计协方差矩阵，而不是依赖经验协方差估计量（具有潜在的收缩）。对象应该有一个拟合方法和一个协方差属性，如sklearn.covariance的估计器。 如果没有，收缩参数驱动估计。如果使用收缩率，则应将其保留为“None”。注意协方差估计只适用于lsqr和特征解算器。

属性	解释
coef_：ndarray of shape (n_features,) or (n_classes, n_features)	权重向量
intercept_：ndarray of shape (n_classes,)	截距项
covariance_：array-like of shape (n_features, n_features)	类内加权协方差矩阵。它对应于$su{m}_{k}prio{r}_k\ast C_k$其中$C_k$是k类样本的协方差矩阵。$C_k$使用协方差的（潜在收缩）有偏估计量来估计。如果解算器为“svd”，则仅当store_covariance为True时才存在。
explained_variance_ratio_：ndarray of shape (n_components,)	由每个所选组成部分解释的方差百分比。如果未设置n_components，则存储所有分量，解释的方差之和等于1.0。仅当使用eigen或svd解算器时可用。
means_：array-like of shape (n_classes, n_features)	Class-wise means.
priors_：array-like of shape (n_classes,)	类优先级（总和为1）。
scalings_：array-like of shape (rank, n_classes - 1)	类质心所跨越的空间中特征的缩放。仅适用于“svd”和“特征”解算器。
xbar_：array-like of shape (n_features,)	总体平均值。仅当“解算器”为“svd”时才存在。
classes_：array-like of shape (n_classes,)	唯一的类标签。

方法	解释
decision_function(X)	对样本数组应用决策函数。
fit(X, y[, sample_weight])	拟合模型
fit_transform(X[, y])	拟合数据再转换它
get_params([deep])	获取此估计器的参数。
predict(X)	预测
predict_log_proba(X)	估计对数概率。
predict_proba(X)	估计概率
score(X, y[, sample_weight])	返回给定测试数据和标签的平均精度。
set_params(**params)	设置此估计器的参数。
transform(X)	项目数据以最大化类分离。

例子：

>>> import numpy as np
>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = LinearDiscriminantAnalysis()
>>> clf.fit(X, y)
LinearDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]

sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis

参数	解释
priors：array-like of shape (n_classes,), default=None	类先验概率。默认情况下，类比例是从训练数据中推断出来的。
reg_param：float, default=0.0	通过将S2转换为$S2=(1-re{g}_{p}aram)\ast S2+re{g}_{p}aram\ast np.eye(n_{f}eatures)$对每类协方差估计进行正则化，其中$S2$对应于给定类的scaling_ 属性。
store_covariance：bool, default=False	如果为True，类协方差矩阵将显式计算并存储在self.covariance_属性
tol：float, default=1.0e-4	奇异值被视为显著值的绝对阈值，用于估计Xk的秩，其中Xk是k类中样本的中心矩阵。此参数不影响预测。它只控制当特征被认为是共线时发出的警告。

属性	解释
covariance_：list of len n_classes of ndarray of shape (n_features, n_features)	对于每个类，给出使用该类的样本估计的协方差矩阵。估计是无偏的。仅当存储协方差为真时才显示。
means_：array-like of shape (n_classes, n_features)	Class-wise means.
priors_：array-like of shape (n_classes,)	类优先级（总和为1）。
rotations_：list of len n_classes of ndarray of shape (n_features, n_k)	对于每个k类，一个形状数组（n_features，n_k），其中n_k = min(n_features, number of elements in class k)，它是高斯分布的旋转，即其主轴。它对应于V，来自Xk = U S Vt的奇异值分解的特征向量矩阵，其中Xk是k类样本的中心矩阵。
scalings_：list of len n_classes of ndarray of shape (n_k,)	对于每个类，包含沿其主轴的高斯分布的缩放比例，即旋转坐标系中的方差。它对应于S^2 / (n_samples - 1)，其中S是Xk的奇异值的对角矩阵，其中Xk是k类样本的中心矩阵。
classes_：array-like of shape (n_classes,)	唯一的类标签。

方法	解释
decision_function(X)	对样本数组应用决策函数。
fit(X, y[, sample_weight])	拟合模型
get_params([deep])	获取此估计器的参数。
predict(X)	预测
predict_log_proba(X)	估计对数概率。
predict_proba(X)	估计概率
score(X, y[, sample_weight])	返回给定测试数据和标签的平均精度。
set_params(**params)	设置此估计器的参数。

例子：

>>> from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = QuadraticDiscriminantAnalysis()
>>> clf.fit(X, y)
QuadraticDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]

1.2.1. 使用线性判别分析来降维

discriminant_analysis.LinearDiscriminantAnalysis 通过把输入的数据投影到由最大化类之间分离的方向所组成的线性子空间，可以执行有监督降维（详细的内容见下面的数学推导）。输出的维度必然会比原来的类别数量更少的。因此它总体而言是十分强大的降维方式，同样也仅仅在多分类环境下才能感觉到。

实现方式在discriminant_analysis.LinearDiscriminantAnalysis.transform中。关于维度的数量可以通过 n_components参数来调节。 值得注意的是，这个参数不会对 discriminant_analysis.LinearDiscriminantAnalysis.fit 或者 discriminant_analysis.LinearDiscriminantAnalysis.predict 产生影响。

1.2.2. LDA 和 QDA 分类器的数学公式

LDA和 QDA 都是源于简单的概率模型，这些模型对于每一个类别 k 的相关分布P(X|y=k) 都可以通过贝叶斯定理所获得。
$$P(y=k|X)=\frac{P(X|y=k)P(y=k)}{P(X)}=\frac{P(X|y=k)P(y=k)}{{\sum }_{l}P(X|y=l)\cdot P(y=l)}$$
我们选择最大化条件概率的类别 k.

更具体地说，对于线性以及二次判别分析， P(X|y) 被建模成密度多变量高斯分布:
$$p(X|y=k)=\frac{1}{(2\pi {)}^n|{\Sigma }_k{|}^{1/2}}\exp \left(-\frac{1}{2}(X-{\mu }_k{)}^t{\Sigma }_k^{-1}(X-{\mu }_k)\right)$$
其中的d是特征数量

为了把该模型作为分类器使用，我们只需要从训练数据中估计出类的先验概率P(y=k)（通过每个类 k 的实例的比例得到） 类别均值 ${\mu }_k$ （通过经验样本的类别均值得到）以及协方差矩阵（通过经验样本的类别协方差或者正则化的估计器 estimator 得到: 见下面的 shrinkage 章节）。

在LDA 中，每个类别k的高斯分布共享相同的协方差矩阵:${\Sigma }_k$。这导致了两者之间的线性决策面，这可以通过比较对数概率比看出来
$$\log [P(y=k|X)/P(y=l|X)]$$
$$\log \left(\frac{P(y=k|X)}{P(y=l|X)}\right)=0\iff ({\mu }_k-{\mu }_l){\Sigma }^{-1}X=\frac{1}{2}({\mu }_k^t{\Sigma }^{-1}{\mu }_k-{\mu }_l^t{\Sigma }^{-1}{\mu }_l)$$
在QDA中，没有关于高斯协方差矩阵 ${\Sigma }_k$ 的假设，因此有了二次决策平面. 更多细节见 参考文献[3].

注意:与高斯朴素贝叶斯的关系
如果在QDA模型中假设协方差矩阵是对角的，则输入被假设为在每个类中是条件独立的，所得的分类器等同于高斯朴素贝叶斯分类器 naive_bayes.GaussianNB 相同。

1.2.3. LDA 的降维数学公式

为了理解LDA在降维上的应用，从上面解释的 LDA 分类规则的几何重构开始是十分有用的。我们用 $K$ 表示目标类别的总数。 由于在 LDA 中我们假设所有类别都有相同估计的协方差 $\Sigma$ ,所以我们可重新调节数据从而让协方差相同。
$$X^{\ast }=D^{-1/2}{U}^{t}X\text{ with }\Sigma =UD{U}^t$$
在缩放之后对数据点进行分类相当于找到与欧几里得距离中的数据点最接近的估计类别均值。但是它也可以在投影到$K-1$个由所有类中的所有${\mu }_k^{\ast }$ 生成的仿射子空间$H_K$ 之后完成。这也表明，LDA 分类器中存在一个利用线性投影到$K-1$ 个维度空间的降维工具。

通过投影到线性子空间 $H_L$ 上，我们可以进一步将维数减少到一个选定的 L ，从而使投影后的 ${\mu }_k^{\ast }$ 的方差最大化（实际上，为了实现转换类均值 ${\mu }_k^{\ast }$，我们正在做一种形式的 PCA）。 这里的 $L$ 对应于 discriminant_analysis.LinearDiscriminantAnalysis.transform 方法中使用的 n_components 参数。 详情参考 参考文献[3] 。

1.2.4. Shrinkage（收缩）

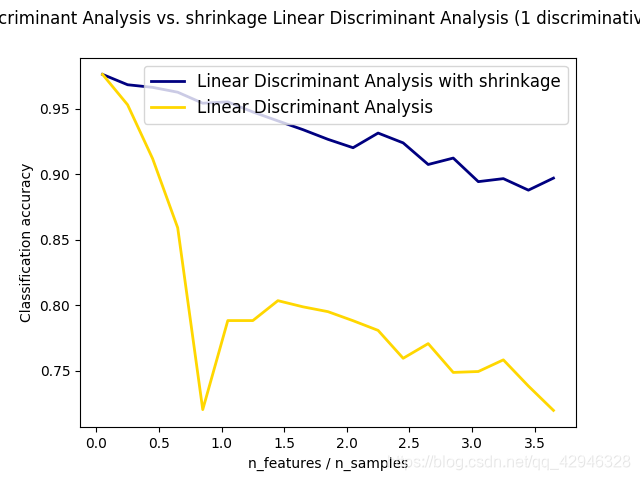
收缩是一种在训练样本数量相比特征而言很小的情况下可以提升的协方差矩阵预测（准确性）的工具。 在这个情况下，经验样本协方差是一个很差的预测器。收缩 LDA 可以通过设置 discriminant_analysis.LinearDiscriminantAnalysis 类的 shrinkage 参数为 ‘auto’ 来实现。

shrinkage parameter （收缩参数）的值同样也可以手动被设置为 0-1 之间。特别地，0 值对应着没有收缩（这意味着经验协方差矩阵将会被使用）， 而 1 值则对应着完全使用收缩（意味着方差的对角矩阵将被当作协方差矩阵的估计）。设置该参数在两个极端值之间会估计一个（特定的）协方差矩阵的收缩形式

1.2.5. 预估算法

默认的 solver 是 ‘svd’。它可以进行classification (分类) 以及 transform (转换),而且它不会依赖于协方差矩阵的计算（结果）。这在特征数量特别大的时候十分具有优势。然而，’svd’ solver 无法与 shrinkage （收缩）同时使用。

lsqr solver 则是一个高效的算法，它仅用于分类使用。它支持 shrinkage （收缩）。

eigen（特征） solver是基于 class scatter （类散度）与 class scatter ratio （类内离散率）之间的优化。 它可以被用于 classification （分类）以及 transform （转换），此外它还同时支持收缩。然而，该解决方案需要计算协方差矩阵，因此它可能不适用于具有大量特征的情况。