目录
二元运算
二元运算基本概念
运算的概念
整数集合上的相反数运算
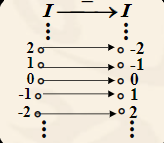
自然数集合上的加法运算
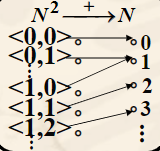
集合中任何一个或两个元素都可以进行运算,且运算的结果唯一。
运算的概念

减法不是自然数集合N上封闭的二元运算
除法不是整数集合I上的二元运算
除法是实数集合R上的封闭的二元运算
运算的表示及运算表

运算表:用来表示有穷集合上的运算
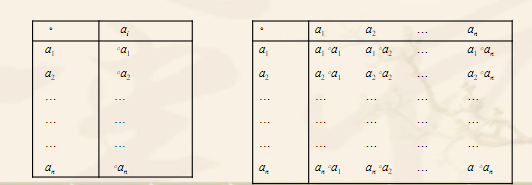

二元运算的性质
封闭性:
设 * 是X上的二元运算,如果对任何的x,y∈X,有x * y∈X,则称*在X上封闭。
例如,自然数集合N上的加法和乘法封闭,而减法不封闭。从运算表可以很容易看出运算是否封闭。
如何观察运算表是否封闭。
运算表中没有出现新元素
交换性
设 * 是X上的二元运算,如果对任何的x,y∈X,有x * y∈y * x,则称*在X上可交换。
加法、乘法、交、并、对称差是可交换。

如果一个运算表是以主对角线对称的,那么这个运算具有可交换性。
可结合性
设 * 是X上的二元运算,如果对任何的x,y,z∈X,有(x * y) * z∈x * (y * z),则称*在X上可交换。
下列运算是可结合的:
数值的加法、乘法,集合的交、并、对称差,关系的复合、函数的复合,命题的合取、析取。
若★是可结合的运算,元素x的★运算,通常可以写成乘幂的形式。如下:
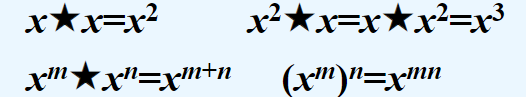
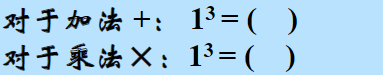
分配律
设★和 * 都是X上的二元运算,若对任何x,y,z∈X, 有
x ★ (y * z)=(x★y) * (x★z) (左分配律)
(x * y)★z=(x★z) * (y★z) (右分配律)
则称★ 对 * 可分配
分配律一定是两个运算,并且同时满足左分配和右分配。并且还要考虑谁对谁分配括号外面对括号里面的可分配。
例如:乘法对加法可分配。集合的U与∩互相可分配。命题的析取与合取 互相可分配。
吸收律
设★和 * 都是X上的二元运算,若对任何x,y∈X, 有
x ★ (x * y)=x
x * (x ★ y)=x
则称★和 * 满足吸收律
例如:集合的U与∩满足吸收律。命题的析取与合取 满足吸收律

数学中的证明有两种方式,比如这里我们可以用定义去证明,用定义证明我们首先要知道什么是可封闭、可结合、可分配。第二种方式是用定理去证明,而我们这里只是学习了定义,明白了这些定义之后,我们的证明就比较简单了。


运算性质小结

二元运算中的特殊元素
幂等元
设★是X上的二元运算,如果有a∈X,满足a★a=a,则称a是X上关于★运算的幂等元。如果对任何x∈X,都有.x★x=x, 则称★在X上有幂等性。
如∩运算具有幂等性
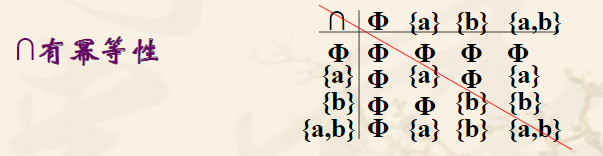
主对角线的元素与.上表头(或左表头)元素相同,则具有幂等性
幺元
设★是X上的二元运算,如果有eL∈X,使得对任何x∈X,均有eL★=x,则称eL是相对★的左幺元。
如果有eR∈X,使得对任何x∈X,均有x*eR=x,则称eR是相对★的右幺元
如果eL=eR=e,对任何x∈X,均有x★e=e★x=x,则称e是相对★的幺元。
幺元又可以称为单位元,恒等元。
●实数集合R上的加法+运算,幺元是0;
因为0+a=a+0=a (a为任意实数)
●乘法X运算,幺元是1;

减法不存在幺元,但存在右幺元

定理


x映射到y端,是唯一的。x端固定,那么y必定唯一。
零元
设★是X上的二元运算,如果有θL∈X,使得对任何x∈X,有θL★x=θL,则称θL是相对★的左零元。
如果有θR∈X,使得对任何x∈X,有x★θR=θR,则称θR是相对★的右零元
如果有θL=θR=θ,对任何x∈X,有θ★x=x★θ=θ,称θ是相对★的零元
例如:实数集合上的乘法X,零元是0;
因为aX0=0Xa=0 (a为任 意实数)
集合族上的并运算∪,零元是全集E
集合族上的交运算∩,零元是∅;

设★是X上的二元运算,如果有左零元θL∈X,也有右零元θR∈X,则θL=θR=θ,且零元θ是唯一的。
设★是集合X上的二元运算,且|X|>1。如果该代数系统中存在幺元e和零元θ,则θ≠e
证明:用反证法。
假设θ=e,那么对任意
x∈X, 必有x=e★x=θ★x=θ=e
这说明X中的所有元素都是相同的,所以θ≠e
逆元
设★是X上有幺元e的二元运算,x∈X,如果有xL-1∈X,使得xL-1★x=e,则称xL-1是x相对★的左逆元
如果有xR-1∈X,使得x★xR-1=e,则称xR-1是x相对★的右逆元。
如果xL-1=xR-1=x-1,有x-1★x=x★x-1=e,称x-1是x相对★的逆元。也称x-1与x互为逆元。如x-1∈X,也称x可逆。
注意:逆元一定要有幺元,且逆元一定要涉及到某个元素。
例:实数集合R上的+和X,x∈R
对加法+:x-1=-x
因为e=0,x+(-x)=0
对乘法X: x-1=1/x (x≠0)
因为e=1,x X 1/x=1

逆元唯一性定理
设★是X上有幺元e且可结合的二元运算,如果x∈X, x的左、右逆元都存在,则x的左、右逆元必相等,且x的逆元是唯一的。

二元运算的其它性质
设★是X上的二元运算,a∈X,如果对任何x,y∈X,有(a★x=a★y)=>x=y或者
(x★a=y★a)=>x=y。
则称a是相对★的可消去元。
如果对任何 a∈X并且a≠θ,a均是可消去元,则称★运算在X上有可消去性。
例如乘法运算,对任意实数a≠0,a就是可消元。
因为当a≠0,若ax=ay则有x=y。
所以乘法在实数集合上有可消去性。
而集合族上的∪和∩运算都不满足可消去性。
因为AUB= AUC或A∩B= A∩C,
不一定有B=C。
设★是X上可结合的二元运算,如果a∈X,且a-1∈X, 则a是可消元。
二元运算的特殊元小结

例:下面是三个运算表
(1) 说明那些运算是可交换的、可结合的、幂等的.
(2) 求出每个运算的幺元、零元、所有可逆元素的逆元
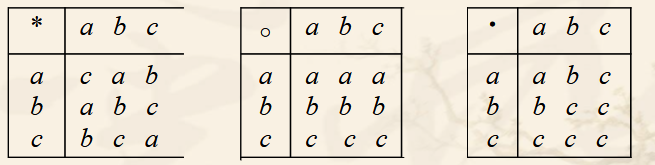
解: (1)*运算满足交换律、结合律,不满足幂等律.
(2)o运算不满足交换律,满足结合律,满足幂等律.
(3).运算满足交换律,满足结合律,不满足幂等律.
说明:关于结合律的判断,需要针对运算元素的每种选择进行验证,若|A|=n, 一般需要验证n3个等式。
单位元和零元不必参与验证.
通过对具体运算性质的分析也可能简化验证的复杂性。

代数系统的基本概念
代数系统的概念
X是非空集合,X及X上的m个运算,f1,f2,…fm构成代数系统U,记作U=<X, f1,f2…fm.> ( m>=1)
U=<X, f1,f2,…,fm>是个代数系统,如果X是个有限集合,则称U是有限代数系统。
给定两个代数系统U=<X, f,fz…,.fm>,V=<Y, g1,g2…,gm>, 如果对应的运算fi和gi的元数相同(i=1,2,3,…m),则称U与V是同类型代数系统。
代数系统的同态与同构
观察下面两个代数系统

R为实数集合,R+为大 于0的实数集合,X、+为普通的实数乘法、加法运算。表面上看这两个代数系统完全不同,实际它们运算的性质却完全一样,都满足:可交换、可结合、有幺元、每个元素可逆。
如何能看出它们间有相同的性质呢?


注意:同态一定是一个映射,这个映射涉及到两个代数系统,是从X到Y的映射,并且要满足一个同态关系式。
如果f是满射的,称此同态是满同态。
如果f是入射的,称此同态是单一同态。
如果f是双射的,称此同态是同构,记作X≌Y。
若f是<X,★>到<X,★>的同态(同构),则称之为自同态(自同构)。



注意:代数系统<X,★>和<Y,o>同构的必要条件:
- X和Y的基数相同,即K[X]=K[Y]。
- 运算★和o是同类型的。
- 存在双射f:X→Y,且满足同构关系式。
并不是所有的双射f:X->Y都满足同构关系式。
在构造双射时,要注意:
幺元与幺元对应;零元与零元对应;
逆元也要相互对应。
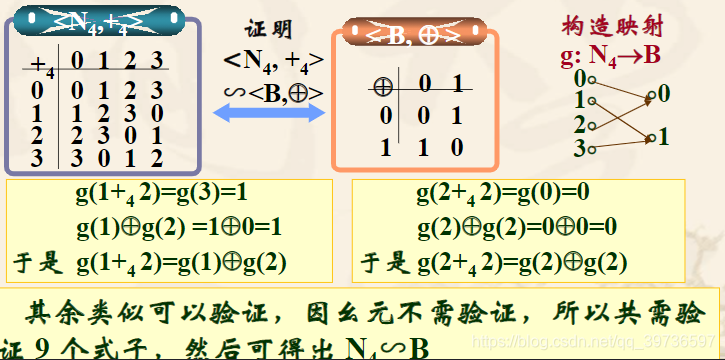
含有两个运算的代数系统的同构

代数系统间的同构关系≌是等价关系。
证明时我们要考虑什么是等价关系,关系满足自反、对称、传递。然后证明同构关系是自反、对称、传递。
代数系统同构的性质
两个同构的代数系统,一些运算性质是可保持的。
即在<X,★>中有的一些运算性质在<Y,o>中也有,反之亦然。
保持可结合性
1)如果运算★在X中可结合,则o在Y中也可结合。

保持可交换性
2)如果运算★在X中可交换,则o在Y中也可交换
证明的方法与1)类似。大家自己证明。
保持幺元存在性
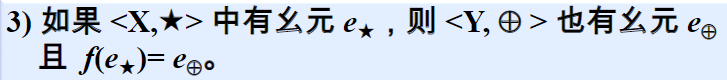
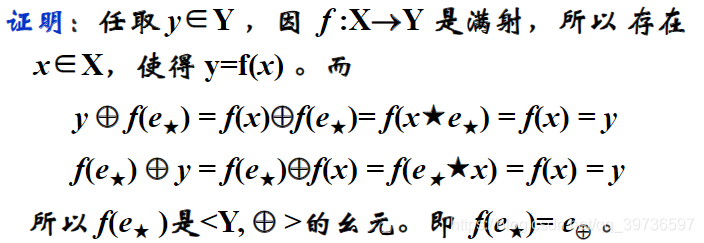
保持零元存在性

保持逆元存在性

保持分配律

保持吸收律
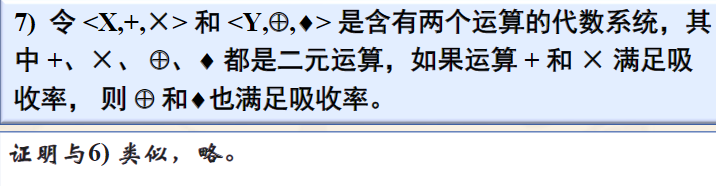
同构性质的保持是双向的,即Y中运算的性质也可以保持到X中运算。
由于同态关系的不满足对称性,所以同态性质的保持只是单向的。即Y中○的性质,X中★不一定有。
代数系统同构的性质