Matlab数字图像处理学习记录【6】——小波

零.前言

在对数字图像进行多分辨率观察和处理时，离散小波变换DWT是首选的数学工具。它还能够帮助我们深入了解图像的空间域和频域特性。

一.背景知识

对一个大小为M×N的图像f(x,y)，其正向离散变换T(u,v,…)可以用一般的多项式关系表示
$$T(u,v,...)=\sum _{x,y}f(x,y)g_{u,v,...}(x,y)$$
其中，x和y为空间变量，而u,v,...是变换域变量。若给定T(u,v,…)则有f(x,y)可用的一般的离散反变换得到
$$f(x,y)=\sum _{u,v,...}T(u,v,...)h_{u,v,...}(x,y)$$
其中g_u,v和h_u,v,…为正变换核和反变换核。他们决定变换对的性质、计算复杂度和主要用途。
变换系数T(u,v,…)可看做是f关于{h_u,v,…}的一系列展开数。
换言之，反变换核对于f的序列展开定义一组展开函数。
DFT与序列展开表示法完全吻合，这种情况下：
$$h_{u,v}(x,y)=g_{u,v}^{\ast }(x,y)=\frac{1}{\sqrt{MN}}{e}^{j2\pi (ux/M+vy/N)}$$
其中，j是虚数单位，*是复共轭运算符。该变换域的v和u分别表示水平频度和垂直频度。变换核是可分的：
$$h_{u,v}(x,y)=h_u(x)h_v(y)$$
$$h_u(x)=\frac{1}{\sqrt{M}}{e}^{j2\pi ux/M}和h_v(y)=\frac{1}{\sqrt{N}}{e}^{j2\pi vy/N}$$
且该两个分量是正交的，因为：
$$⟨h_r,h_s⟩={\delta }_{rs}=\{\begin{array}{ll}1,& r=s\\ 0,& 其他\end{array}$$
变换核的可分性简化了二维变换的计算，因为这样我们就可以对行分开进行一维变换来实现二维变换。正交性则导致了正反变换核之间的复共轭关系。
与离散傅里叶变换不同,离散傅里叶变换完全可以通过关于一对(前面已给出的）变换核的两个简单方程来定义,而术语“离散小波变换”指的是这样一类变换：
不仅其中使用的变换核不同(例如，所用的展开函数)，而且这些函数（例如，不管它们构成正交基还是双正交基）的基本特性和它们应用的方法（例如，计算多少不同的分辨率)也不同。因为DWT包含各种独特但相关的变换，所以我们不能写出一个能完全描述它们的公式。相反,我们利用变换核对或定义该核对的一组参数来表征每个DWT。各种变换都与这样的事实有关，即变换的展开函数是变化频率和持续时间受限的“小波”。
傅里叶展开后，是由无穷个在持续时间无限的正弦波
DWT展开后，是持续时间有限变化的小波

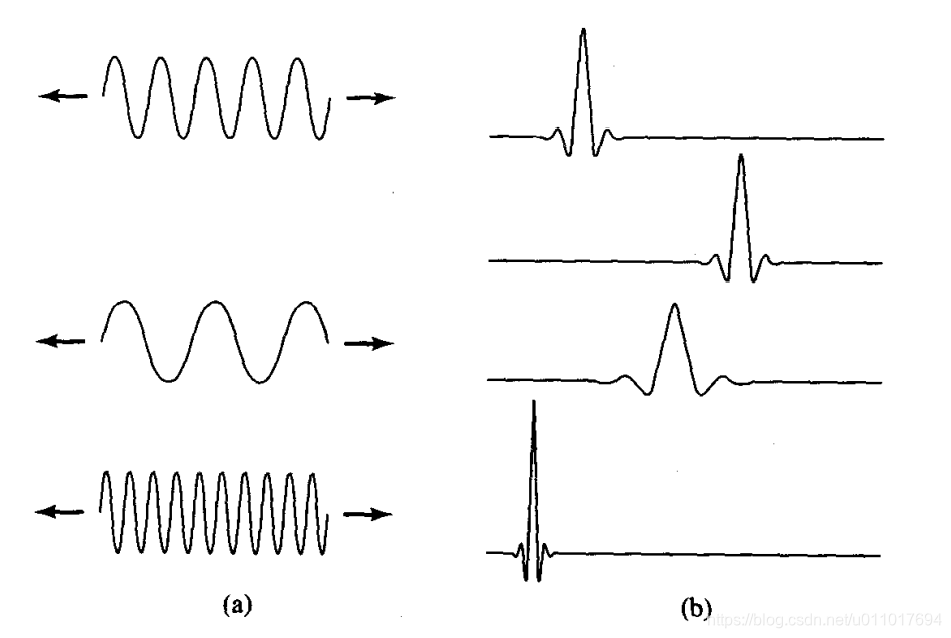
在本章剩余的部分，将介绍几种小波核。每一个小波核都有如下的基本特性：

1. 可分离性、尺度可变性和平移性。核可用三个可分的二维小波表示
   $$\begin{gathered} {\psi }^H(x,y)=\psi (x)\phi (y) \\ {\psi }^V(x,y)=\phi (x)\psi (y) \\ {\psi }^D(x,y)=\psi (x)\psi (y) \end{gathered}$$
   这三者从上到下依次被称为：水平、垂直和对角小波，且二维可分的尺度函数是
   $$\phi (x,y)=\phi (x)\phi (y)$$
   每个二维函数是两个一维实平方可积的尺度和小波函数的乘积：
   $$\begin{gathered} {\phi }_{j,k}(x)=2^{j/2}\phi (2^{j}x-k) \\ {\psi }_{j,k}(x)=2^{j/2}\psi (2^{j}x-k) \end{gathered}$$
   平移参数k决定一位函数沿x轴的位置，尺度j决定宽度。2^{j/2}控制他们的高度和振幅。
2. 多分辨率的一致性。刚才介绍的一维尺度函数满足多分辨率分析的如下需求：

• φ_j,k与其整数平移正交
• 在低尺度下可表示为一系列φ_j,k展开的一组函数，包含在可以以更高尺度表示的那些函数中。
• 唯一可以任意尺度表示的函数是f(x)=0
• 当j→∞时，可以用任意精度来表示任意函数。
  当这些条件满足是，就存在一个伴随小波ψ_j,k及其整数平移和二进制尺度，其变化范围是在邻接尺度上可以表示的任意两组φ_j,k之间的差。

3. 正交性。 展开函数（如{φ_j,k(x)}）对于一组一维可测的、平方可积函数形成一个正交基或双正交基。之所以称为基，是因为对于每一个可描述函数必须有惟一一组展开系数。正如在介绍傅里叶核时所说明的那样,对于实数来说正交核为g_u,v,… = h_u,v,…。对于双正交情况
   $$⟨h_r,h_s⟩={\delta }_{rs}=\{\begin{array}{ll}1,& r=s\\ 0,& 其他\end{array}$$
   并且g成为h的对偶。对于利用尺度和小波函数φ_j,k(x)和ψ_j,k(x)的双正交小波变换。对偶分别定义为${\tilde{\phi }}_{j,k}(x)和{\tilde{\psi }}_{j,k}(x)$

说了那么多小波的性质，个人理解为：通过一种固定的信号(小波核)，且该信号在时域上均值为0的，去“匹配”给定信号。通过二分法缩放其持续时间，来修改其频率。而又通过平移来修改小波在时域上“波动的位置”。这样能够更好的提取某个信号的某时段的频率信息，而不是单纯的像傅里叶那样得到一个频谱。感觉就像是将在变换函数中，加入了可调节窗口大小的特殊的傅里叶变换。

二. 快速小波变换

上面性质的一个重要结果是φ(x)和ψ(x)可以用它们自身的双分辨率副本的线性组合来表达。这样序列展开后：
$$\begin{gathered} \phi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x-n) \\ \psi (x)=\sum _n{h}_{\psi }(n)\sqrt{2}\phi (2x-n) \end{gathered}$$
其中，h_φ和h_ψ展开系数分别称为尺度和小波向量。它们是快速小波变换FWT滤波器的系数。DWT的迭代计算方法如图所示：

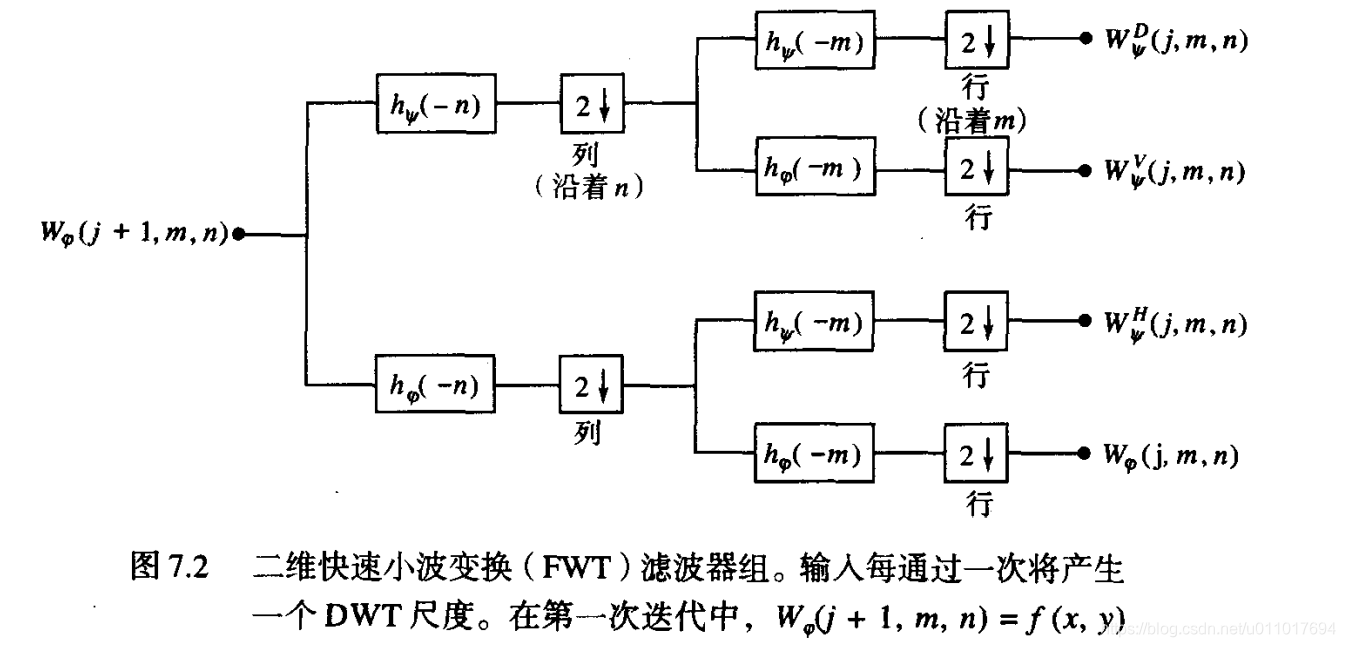
在途中，输出W_φ(j,m,n)和{W_ψⁱ(j,m,n)，i=H,V,D}是在迟钝j处的DWT系数。方框中包含了时间反转尺度和小波向量。单元h_φ(-n)和h_ψ(-m)分别是低通和高通分解滤波器。最后最后，包括2和向下箭头的方框表示下取样，即从点的序列中每隔一个点来提取一个点。准确地说，用于计算图7.2中的W_ψH(i, m, n)的滤波和下取样操作是：
$$W_{\psi }^H(j,m,n)=h_{\psi }(-m)\ast [h_{\phi }(-n)\ast W_{\phi }(j+1,m,n){|}_{n=2k,k\ge 0}]{|}_{m=2k,k\ge 0}$$
其中，*表示卷积。在非负处计算卷积时，偶数索引等价于滤波和用2下取样。

2.1 使用小波工具箱的快速小波变换

小波工具箱对于各种快速小波变换提供了分解滤波器。与特殊变换有关的滤波器可以通过wfilters来访问：
[Lo_D, Hi_D, Lo_R, Hi_R] = wfilters(wname)
其中，输入参数wname决定返回的滤波器系数。输出四个行向量，他们分别是低通分解、高通分解、低通重构、高通重构滤波器。
频繁地耦合的滤波器可以用如下语句交替检索：
[F1, F2] = wfilters(wname, type)
将type设为d、r、l、h可以分别或得一堆分解、重构、低通和高通滤波器。被分解或低通滤波器在F1里返回，重构或高通放在F2中。

上表列出了包含在小波工具箱中的FWT滤波器。它们的性质以及其他与尺度和小波函数相关的信息可在数字滤波和多分辨率分析方面的文献中找到。一些更重要的特性由小波工具箱的函数waveinfo和wavefun提供。例如，为了在MATLAB的命令窗口打印小波族wfamily，可输入waveinfo(wfamily)
标准正交变换的尺度或小波函数的函数的数字近似只，可通过：[phi, psi, xval] = wavefun(wname, iter)获得，返回近似向量φ和ψ并且计算向量xval。参数iter控制迭代次数，决定近似值的精度。对于双正交变换，合适的语法为：
[phi1, psi1, phi2, psi2, xval] = wavefun(wname， iter)
phi1和psi1是分解函数，phi2和psi2是重构函数
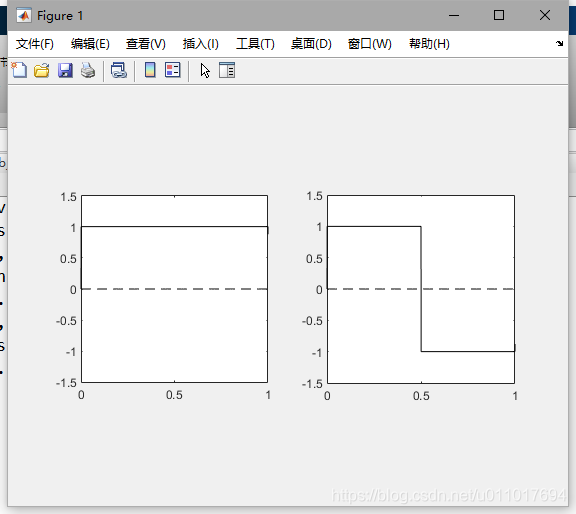
通过以下代码我们能够查询一个小波函数的图形：

[phi, psi, xval] = wavefun('haar', 10);
xaxis = zeros(size(xval));
subplot(1, 2, 1);
plot(xval, phi, 'k', xval, xaxis, '--k');
axis([0 1 -1.5 1.5]); axis square;
subplot(1, 2, 2);
plot(xval, psi, 'k', xval, xaxis, '--k');
axis([0 1 -1.5 1.5]); axis square;

然后可以用两种方式对函数进行小波变换：
[C S] = wavedec2(X, N, Lo_D, Hi_D)和[C S] = wavedec2(X, N, wname)
其中X是二维矩阵，N是被计算的尺度，后者要么给出分解后的滤波器，或者是小波的名称。
C是由行向量C——小波变换系数
矩阵S是定义了C中数据排列的记录矩阵S

---

后面就是一些小波变换代码层面的数学应用，由于时间太碎片化，并没有太多时间去认真分析这些，所以将该处内容留存至以后再学。

---

五.图像处理中的小波

这节则是对图像处理的小波的应用。基于小波的图像处理办法过程因该是：

1. 计算一幅图像的而为小波变换
2. 修改变换系数
3. 计算反变换

5.1 方向性和边缘检测

f = imread('./example.tif');
subplot(2, 2, 1);
imshow(f);
subplot(2, 2, 2);
[c, s] = wavefast(f, 1, 'sym4');
wave2gray(c, s, -6);
subplot(2, 2, 3);
[nc, y] = wavecut('a', c, s);
wave2gray(nc, s, -6);
edge = abs(waveback(nc, s, 'sym4'));
subplot(2, 2, 4);
imshow(mat2gray(edge));

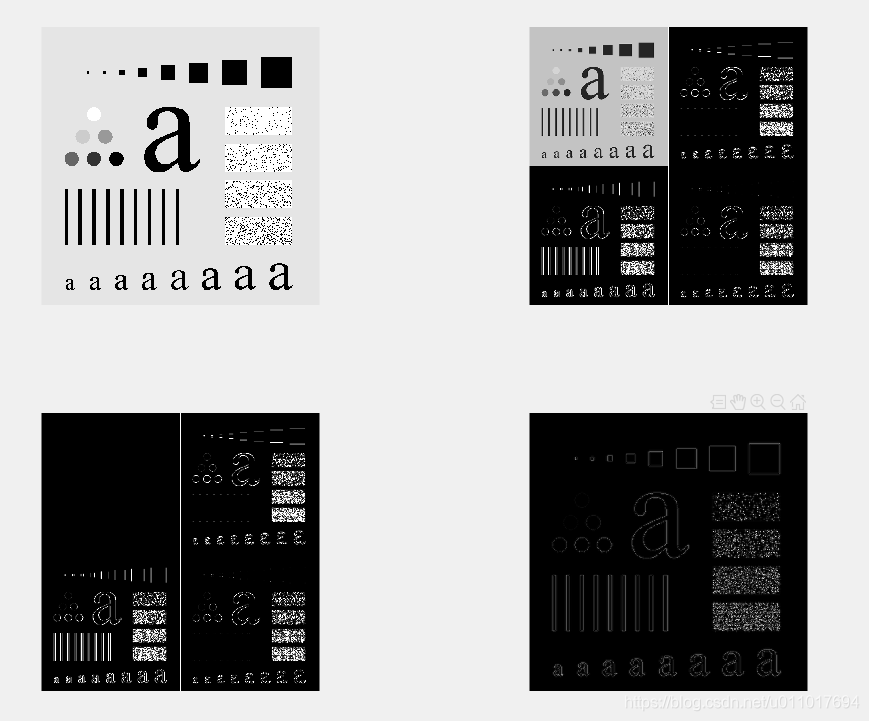
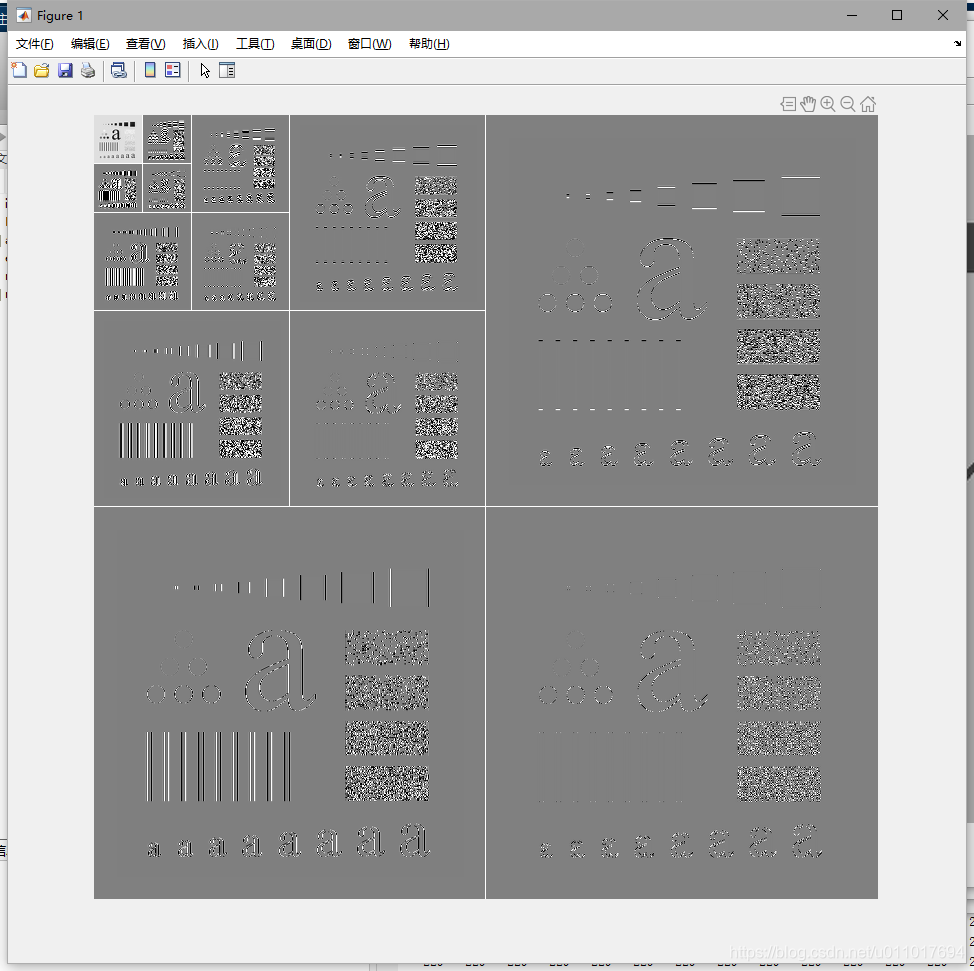
关于’sym4’小波，图1的单尺度小波变换的水平、垂直、对角线的方向性在图2中可清楚地看到。注意，原图像的水平边缘出现在图2的右上象限的水平细节系数中。对于图像的垂直边缘,可以在左下象限的垂直细节系数中类似地确定。要将这些信息合并成为一幅边缘图像，我们可以简单地把生成的变换的近似系数设为零,计算它的反变换,再对其取绝对值。修改过的变换和得到的边缘图像分别显示在图3和图4中。类似的过程可用于隔离垂直边缘或水平边缘。

5.2 图像平滑或模糊

通过wavezero函数 将某一级小波变换的值置0.

function [nc, g8] = wavezero(c, s, l, wname)
%WAVEZERO Zeroes wavelet transform detail coefficients. 
%   [NC, G8] = WAVEZERO(C, S, L, WNAME) zeroes the level L detail
%   coefficients in wavelet decomposition structure [C, S] and
%   computes the resulting inverse transform with respect to WNAME
%   wavelets.

%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
%   $Revision: 1.4 $  $Date: 2003/10/13 01:31:35 $

[nc, foo] = wavecut('h', c, s, l);
[nc, foo] = wavecut('v', nc, s, l);
[nc, foo] = wavecut('d', nc, s, l);
i = waveback(nc, s, wname);
g8 = im2uint8(mat2gray(i));
figure; imshow(g8);

然后通过不断调用wavezero将图片更平滑：

f = imread('./example.tif')
[c, s] = wavefast(f, 4, 'sym4');
wave2gray(c, s, 20);
[c, g8] = wavezero(c, s, 1, 'sym4');
[c, g8] = wavezero(c, s, 2, 'sym4');
[c, g8] = wavezero(c, s, 3, 'sym4');
[c, g8] = wavezero(c, s, 4, 'sym4');

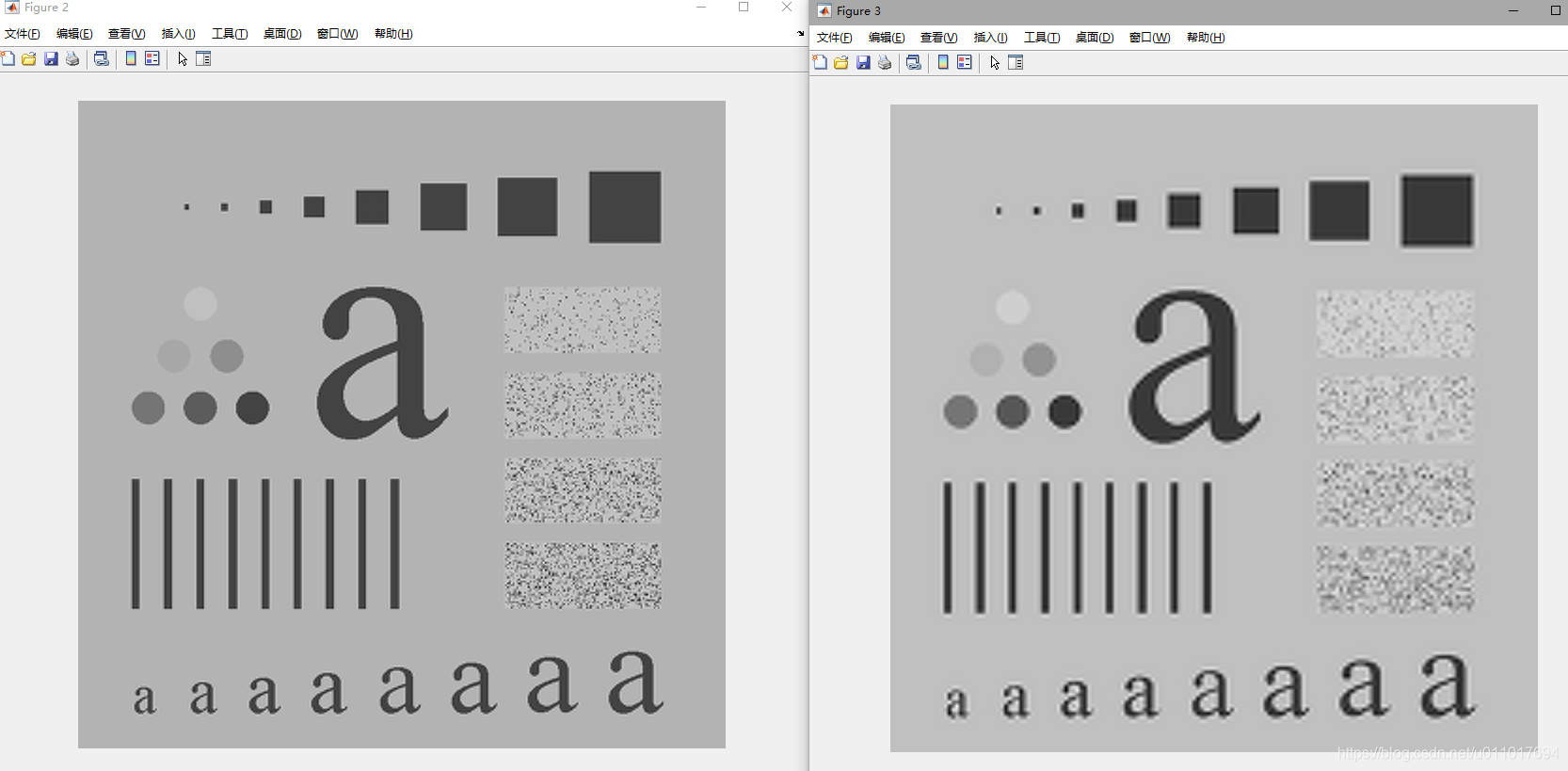
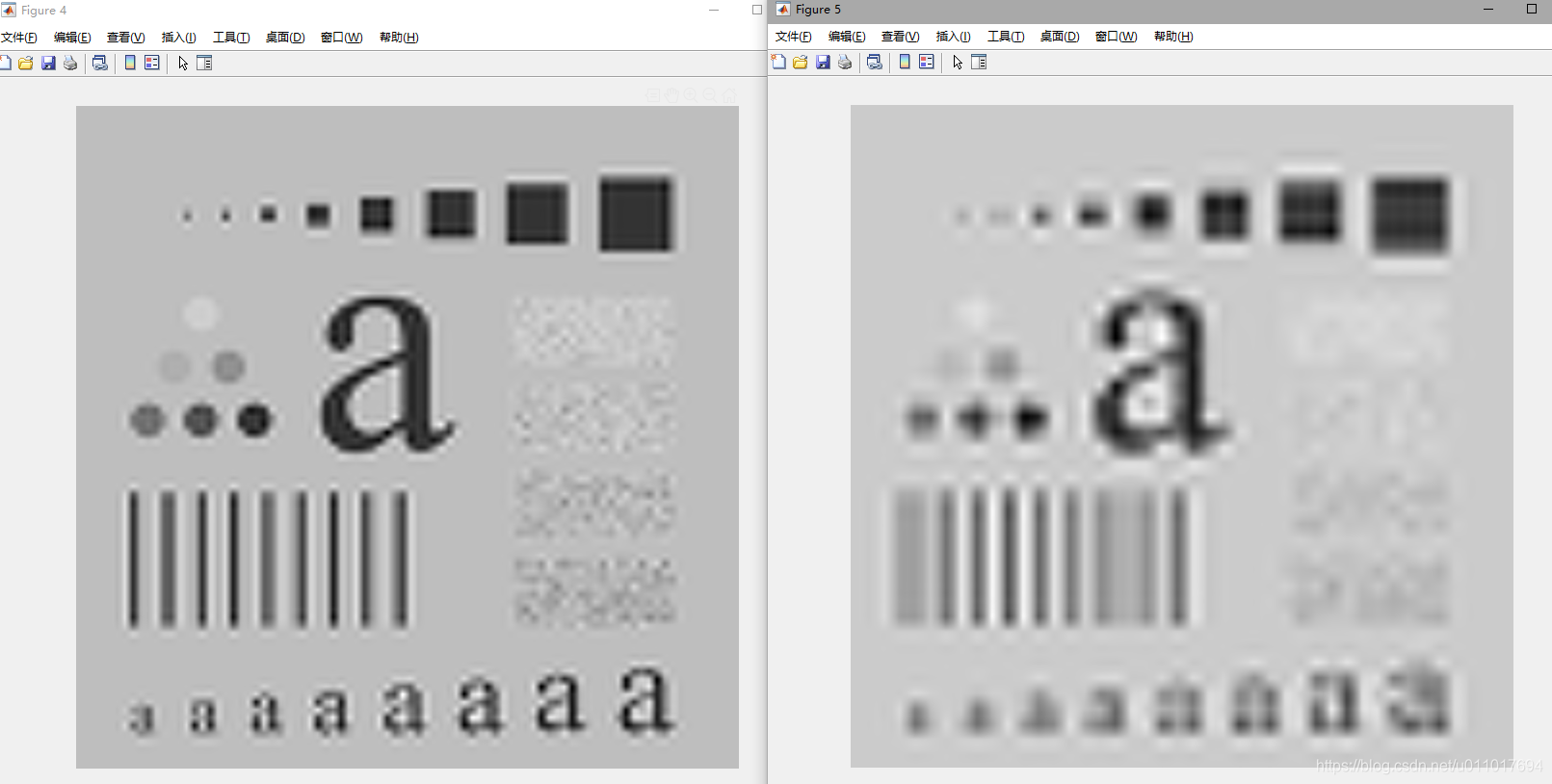
然后发现级数越高模糊程度越高。所以，小波函数域中的尺度和傅里叶域中的频率之间的有着某种联系。