当输入规模足够大,要研究算法的渐近效率,即我们关心当输入规模无限增加时,在极限中,算法的运行时间如何随着输入规模的变大而增加。
主要使用以下渐近记号描述算法的运行时间:
1.θ记号
给定一个函数g(n),用θ(g(n))表示以下函数的集合:

若存在正常量c1和c2,使得对于足够大的n,函数f(n)能夹入c1g(n)与c2g(n)之间,则f(n)属于集合θ(g(n))。
对于所有n>=n0,函数f(n)在一个常量因子内等于g(n),我们称g(n)是f(n)的一个渐近紧确界。

θ记号中的每个函数都渐近非负(即当n足够大时,f(n)非负),本章中其他渐近记号也是如此。
2.O记号
使用O记号表示渐近上界:

f(n)=θ(g(n))蕴含着f(n)=O(g(n))。
对插入排序的最坏运行时间的界θ(n2)并未暗示插入排序对每个输入的运行时间的界也是θ(n²),如当输入已排好序时,插入排序运行时间为θ(n)。
对插入排序的最坏情况运行时间的界O(n²)适用于该算法对每个输入的运行时间。
技术上看,称插入排序的运行时间为O(n²)不合适,因为对于给定n,实际的运行时间是变化的,依赖于规模为n的特定输入,我们说“运行时间为O(n²)”时,意指存在一个O(n²)的函数f(n),使得对n的任意值,不管选择什么特定的规模为n的输入,其运行时间的上界都是f(n),即最坏状况运行时间为O(n²)。
3.Ω记号
Ω记号提供了渐近下界:


插入排序的最好情况运行时间为Ω(n),这蕴含着插入排序的运行时间为Ω(n)。所以插入排序运行时间介于Ω(n)和O(n²)。
4.o记号
由O记号提供的上界可能是也可能不是渐近紧确的,如2n²=O(n²)是渐近紧确的,但2n=O(n²)不是渐近紧确的。我们使用o记号表示一个非渐近紧确的上界:

在o记号中,当n趋于无穷时,函数f(n)相对于g(n)来说变得微不足道了:

5.ω记号
ω记号表示一个非渐近紧确的下界:
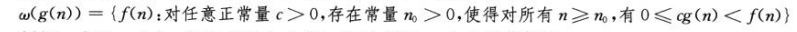
f(n)=ω(g(n))蕴含着:
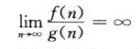

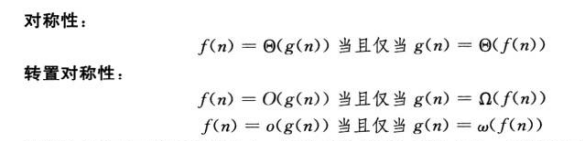
函数f和g的渐近比较和两个实数a与b的比较之间的类比:

然而实数的下列性质不能携带到渐近记号:

对两个函数f(n)和g(n),也许f(n)=O(g(n))和f(n)=Ω(g(n))都不成立,如函数n和n1+sinn。
若f(n)=o(g(n)),则称f(n)渐近小于g(n);若f(n)=ω(g(n)),则称f(n)渐近大于g(n)。
任意底大于1的指数函数比任意多项式函数增长得快。
由换底公式,不同底的对数函数只相差常数倍:
l o g 2 x / l o g 10 x = l o g c x l o g c 10 / l o g c 2 l o g c x = l o g c 10 / l o g c 2 log_{2}x/log_{10}x = log_{c}xlog_{c}10/log_{c}2log_{c}x = log_{c}10/log_{c}2 log2x/log10x=logcxlogc10/logc2logcx=logc10/logc2
其中c为常数。因此当我们不关心这些常量因子时,经常使用记号lgn(如在O记号中)。
对于对数函数,对所有实数a>0,b>0,c>0和n,有:
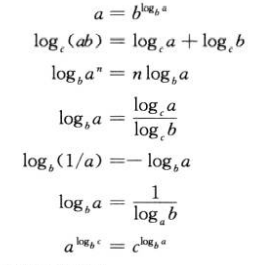
任意正的多项式函数比任意对数函数增长得块。
多重函数:
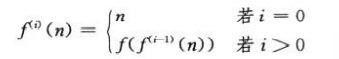
多重对数函数是一个增长非常慢的函数。
斐波那契数列以指数形式增长。