应用例子1:一个总体的方差或标准差检验
双尾检验
【例1】某厂生产一种新型饮料装瓶机器,该机器装一瓶一升(1000cm3)的饮料误差上下不超过1cm3。如果达到设计要求,表明机器的稳定性非常好。先从该机器装完的产品中随机抽取25瓶,分别进行测定(用样本减1000cm3),得到一组数据如下:0.3,-0.4,-0.7,1.4,-0.6,-0.3,-1.5,0.6,-0.9,1.3,-1.3,0.7,1,-0.5,0,-0.6,0.7,-1.5,-0.2,-1.9,-0.5,1,-0.2,-0.6,1.1
现检验该机器的性能是否达到了设计要求?( α = 0.05 α=0.05 α=0.05)
-
建立原假设和备择假设。
H 0 : σ 2 = 1 , H 1 : σ 2 ≠ 1 , α = 0.05 H_0:σ^2=1,H_1:σ^2≠1,α=0.05 H0:σ2=1,H1:σ2=1,α=0.05 -
计算统计量 χ 2 \chi ^{2} χ2值
S 2 = ∑ ( x i − x ‾ ) 2 n − 1 = 0.866 S^2=\frac{\sum(x_{i}-\overline{x})^2}{n-1}=0.866 S2=n−1∑(xi−x)2=0.866
χ 2 = ( n − 1 ) S 2 σ 0 2 = ( 25 − 1 ) ∗ 0.866 1 = 20.8 \chi ^{2}=\frac{(n-1)S^2}{\sigma _{0}^2}=\frac{(25-1)*0.866}{1}=20.8 χ2=σ02(n−1)S2=1(25−1)∗0.866=20.8 -
确定自由度与理论 χ 2 \chi ^{2} χ2值。
d f = n − 1 = 25 − 1 = 24 df=n-1=25-1=24 df=n−1=25−1=24
右 侧 : χ α / 2 2 ( d f ) = χ 0.05 / 2 2 ( 24 ) = 39.36 右侧:\chi_{\alpha/2} ^{2}(df)=\chi_{0.05/2} ^{2}(24)=39.36 右侧:χα/22(df)=χ0.05/22(24)=39.36
左 侧 : χ 1 − α / 2 2 ( d f ) = χ 1 − 0.05 / 2 2 ( 24 ) = 12.40 左侧:\chi_{1-\alpha/2} ^{2}(df)=\chi_{1-0.05/2} ^{2}(24)=12.40 左侧:χ1−α/22(df)=χ1−0.05/22(24)=12.40 -
比较计算所得 χ 2 \chi ^{2} χ2值与理论 χ 2 \chi ^{2} χ2值。
12.40 = χ 1 − 0.05 / 2 2 ( 24 ) < χ 2 = 20.8 < χ 0.05 / 2 2 ( 24 ) = 39.36 12.40=\chi_{1-0.05/2} ^{2}(24)<\chi ^{2}=20.8<\chi_{0.05/2} ^{2}(24)=39.36 12.40=χ1−0.05/22(24)<χ2=20.8<χ0.05/22(24)=39.36
决策:在 α = 0.05 α=0.05 α=0.05的水平上不拒绝 H 0 H_0 H0 ;
结论:该机器的性能达到了要求。

单尾检验
【例2】用机器包装食盐,假设没带盐的净重Xg,服从正态分布 N ( μ , σ 2 ) N(μ,σ^2) N(μ,σ2),规定每袋盐的标准重量为500g,标准差不超过10g。某天开工,为检验机器工作是否正常,随机抽取了9袋盐,测得净重为497,507,510,475,488,524,491,515,484。
问这天该机器的工作是否正常?( α = 0.05 α=0.05 α=0.05)
-
建立原假设和备择假设。
H 0 : μ = μ 0 = 500 , H 1 : μ ≠ μ 0 , α = 0.05 H_0:μ=μ_0=500,H_1:μ≠μ_0,α=0.05 H0:μ=μ0=500,H1:μ=μ0,α=0.05 ( t t t检验,结论是机器包装没有产生系统误差)
H 0 : σ 2 ≤ 1 0 2 , H 1 : σ 2 > 1 0 2 , α = 0.05 H_0:σ^2≤10^2,H_1:σ^2>10^2,α=0.05 H0:σ2≤102,H1:σ2>102,α=0.05 -
计算统计量 χ 2 \chi ^{2} χ2值
S = ∑ ( x i − x ‾ ) 2 n − 1 = 16.03 S=\sqrt{\frac{\sum(x_{i}-\overline{x})^2}{n-1}}=16.03 S=n−1∑(xi−x)2=16.03
χ 2 = ( n − 1 ) S 2 σ 0 2 = ( 9 − 1 ) ∗ 16.0 3 2 1 0 2 = 20.56 \chi ^{2}=\frac{(n-1)S^2}{\sigma _{0}^2}=\frac{(9-1)*16.03^2}{10^2}=20.56 χ2=σ02(n−1)S2=102(9−1)∗16.032=20.56 -
确定自由度与理论 χ 2 \chi ^{2} χ2值。
d f = n − 1 = 9 − 1 = 8 df=n-1=9-1=8 df=n−1=9−1=8
右 侧 : χ α 2 ( d f ) = χ 0.05 2 ( 8 ) = 15.51 右侧:\chi_{\alpha} ^{2}(df)=\chi_{0.05} ^{2}(8)=15.51 右侧:χα2(df)=χ0.052(8)=15.51 -
比较计算所得 χ 2 \chi ^{2} χ2值与理论 χ 2 \chi ^{2} χ2值。
χ 2 = 20.56 > χ 0.05 2 ( 8 ) = 15.51 \chi ^{2}=20.56>\chi_{0.05} ^{2}(8)=15.51 χ2=20.56>χ0.052(8)=15.51
决策:在 α = 0.05 α=0.05 α=0.05的水平上拒绝 H 0 H_0 H0 ;
结论:认为方差超过 1 0 2 10^2 102,即包装机的工作虽没有系统误差,但是不够稳定,因此可认为这天机器工作不够正常。
应用例子2:拟合优度检验
需要检验总体的分布函数F(x)是否等于某个给定的函数 F0(x) ,可以根据经验来进行确定。含有未知参数时,应利用样本资料,采用点估计、极大似然估计求得,再进行检验。
【例3】自1965.1.1至1971.2.9共2231天中,全世界记录里氏震级4级和4级以上地震共162次,统计如下:
试检验相继两次地震间隔天数X服从指数分布( α = 0.05 α=0.05 α=0.05)。
- 建立原假设和备择假设。
H 0 : 总 体 X 的 概 率 密 度 为 f ( x ) = { 1 θ e − x θ ,x>0 0 ,x≤0 , H 1 : 总 体 X 的 概 率 密 度 不 为 f ( x ) H_0:总体X的概率密度为f(x)=\left\{\begin{matrix}\frac{1}{\theta}e^{-\frac{x}{\theta}}\text{,x>0}\\0\text{,x≤0}\\\end{matrix}\right.,H_1:总体X的概率密度不为f(x) H0:总体X的概率密度为f(x)={ θ1e−θx,x>00,x≤0,H1:总体X的概率密度不为f(x)
由于在 H 0 H_0 H0中的参数 θ θ θ没有给出,故要先估计 θ θ θ。
由极大似然估计法得 θ ^ = x ˉ = 2231 162 = 13.77 \hat{θ}=\bar{x}=\frac{2231}{162}=13.77 θ^=xˉ=1622231=13.77, x x x为连续型随机变量 - 求出期望频数与卡方统计量。 将 x x x取值范围 [ 0 , + ∞ ] [0,+∞] [0,+∞]划分成 A 1 , . . . , A 9 A_1,...,A_9 A1,...,A9,落入 A i A_i Ai区间的样本值个数为 f i f_i fi:实测频数,所有实测频数 f 1 + . . . + f k = n ( 样 本 容 量 ) f_1+...+f_k=n(样本容量) f1+...+fk=n(样本容量)。根据所假设的理论分布,我们可以算出落入每个区间 A i A_i Ai的概率 p i p_i pi,于是 n p i np_i npi为 A i A_i Ai区间的 理论频数。

在 H 0 H_0 H0为真的前提下,X的分布函数的估计为
F ^ ( x ) = { 1 − e − x 13.77 ,x>0 0 ,x≤0 \hat{F}(x)=\left\{\begin{matrix}1-e^{-\frac{x}{13.77}}\text{,x>0}\\0\text{,x≤0}\\\end{matrix}\right. F^(x)={ 1−e−13.77x,x>00,x≤0
p i ^ = P ^ ( A i ) = P ^ ( a i ≤ X < a i + 1 ) = F ^ ( a i + 1 ) − F ^ ( a i ) \hat{p_i}=\hat{P}(A_i)=\hat{P}(a_i≤X<a_{i+1})=\hat{F}(a_{i+1})-\hat{F}(a_i) pi^=P^(Ai)=P^(ai≤X<ai+1)=F^(ai+1)−F^(ai)
p 2 ^ = P ^ ( A 2 ) = P ^ ( 4.5 ≤ X < 9.5 ) = F ^ ( 9.5 ) − F ^ ( 4.5 ) = 0.2196 \hat{p_2}=\hat{P}(A_2)=\hat{P}(4.5≤X<9.5)=\hat{F}(9.5)-\hat{F}(4.5)=0.2196 p2^=P^(A2)=P^(4.5≤X<9.5)=F^(9.5)−F^(4.5)=0.2196
p 9 ^ = F ^ ( A 9 ) = 1 − ∑ i = 1 8 F ^ ( A i ) = 0.0568 \hat{p_9}=\hat{F}(A_9)=1-\sum_{i=1}^{8}\hat{F}(A_i)=0.0568 p9^=F^(A9)=1−i=1∑8F^(Ai)=0.0568
χ 2 = ∑ i = 1 k ( f i − n p i ) 2 n p i = 1.5633 \chi ^{2}=\sum_{i=1}^{k}\frac{(f_i-np_i)^2 }{np_i}=1.5633 χ2=i=1∑knpi(fi−npi)2=1.5633 - 确定自由度与理论 χ 2 \chi ^{2} χ2值。
χ 2 > χ α 2 ( k − r − 1 ) = χ α 2 ( 9 − 1 − 1 ) = χ 0.05 2 ( 7 ) = 14.07 \chi ^2>\chi_\alpha^2(k-r-1)=\chi_\alpha^2(9-1-1)=\chi_{0.05}^2(7)=14.07 χ2>χα2(k−r−1)=χα2(9−1−1)=χ0.052(7)=14.07 - 比较计算所得 χ 2 \chi ^{2} χ2值与理论 χ 2 \chi ^{2} χ2值。
χ 2 = 1.5633 < χ 0.05 2 ( 7 ) = 14.07 \chi ^{2}=1.5633<\chi_{0.05}^2(7)=14.07 χ2=1.5633<χ0.052(7)=14.07
决策:在 α = 0.05 α=0.05 α=0.05的水平上接受 H 0 H_0 H0 ;
结论:认为样本服从指数分布。
【例4】某金融系统贷款的偿还类型有四种,各种的预期还率为80%、12%、7%和1%。在一段时间的观察记录中,A型按时偿还的有380笔、B型偿还有69笔、C型有 43笔、D笔有8笔。问这些结果与预期的是否一致( α = 0.05 α=0.05 α=0.05)。
- 建立原假设和备择假设。
H 0 : 结 果 与 预 期 一 致 , H 1 : 结 果 与 预 期 不 一 致 Η_0:结果与预期一致,H_1:结果与预期不一致 H0:结果与预期一致,H1:结果与预期不一致
或
H 0 : P 1 = 80 % , P 2 = 12 % , P 3 = 7 % , P 4 = 1 % , H 1 : P i ≠ P i 0 Η_0:P_1=80\%,P_2=12\%, P_3=7\%, P_4=1\%,H_1:P_i≠P_{i0} H0:P1=80%,P2=12%,P3=7%,P4=1%,H1:Pi=Pi0 - 求出期望频数与卡方统计量。 将总体取值范围划分成 A 1 , . . . , A k A_1,...,A_k A1,...,Ak,落入 A i A_i Ai区间的样本值个数为 f i f_i fi:实测频数,所有实测频数 f 1 + . . . + f k = n ( 样 本 容 量 ) f_1+...+f_k=n(样本容量) f1+...+fk=n(样本容量)。根据所假设的理论分布,我们可以算出落入每个区间 A i A_i Ai的概率 p i p_i pi,于是 n p i np_i npi为 A i A_i Ai区间的 理论频数。
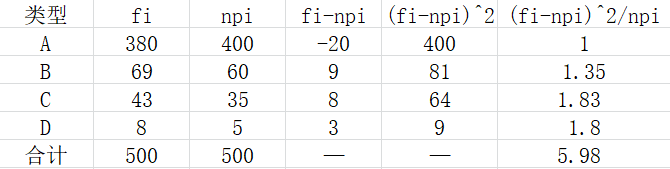
n p 1 = 80 % ∗ 500 = 400 , n p 2 = 12 % ∗ 500 = 60 , n p 3 = 7 % ∗ 500 = 35 , n p 4 = 1 % ∗ 500 = 5 np_1=80\%*500=400,np_2=12\%*500=60,np_3=7\%*500=35,np_4=1\%*500=5 np1=80%∗500=400,np2=12%∗500=60,np3=7%∗500=35,np4=1%∗500=5
χ 2 = ∑ i = 1 k ( f i − n p i ) 2 n p i = 5.98 \chi ^{2}=\sum_{i=1}^{k}\frac{(f_i-np_i)^2 }{np_i}=5.98 χ2=i=1∑knpi(fi−npi)2=5.98
- 确定自由度与理论 χ 2 \chi ^{2} χ2值。
拒 绝 域 : χ 2 > χ α 2 ( k − 1 ) = χ 0.05 2 ( 4 − 1 ) = χ 0.05 2 ( 3 ) = 7.81 拒绝域:\chi ^2>\chi_\alpha^2(k-1)=\chi_{0.05}^2(4-1)=\chi_{0.05}^2(3)=7.81 拒绝域:χ2>χα2(k−1)=χ0.052(4−1)=χ0.052(3)=7.81 - 比较计算所得 χ 2 \chi ^{2} χ2值与理论 χ 2 \chi ^{2} χ2值。
χ 2 = 5.98 < χ 0.05 2 ( 3 ) = 7.81 \chi ^{2}=5.98<\chi_{0.05}^2(3)=7.81 χ2=5.98<χ0.052(3)=7.81
决策:在 α = 0.05 α=0.05 α=0.05的水平上接受 H 0 H_0 H0 ;
结论:认为结果与预期一致,观测的比率与期望的比率一致。
应用例子3:两变量独立性检验
【例5】我们要观察性别和在线上买不买生鲜食品有没有关系( α = 0.1 α=0.1 α=0.1)。
现实生活中,女性通常去菜市场买菜的比较多,那么在线上是不是也这样。
- 建立原假设和备择假设。
H 0 : “ 性 别 ” 与 “ 在 线 上 买 不 买 生 鲜 食 品 ” 之 间 无 关 , H 1 : 两 变 量 之 间 有 关 H_0:“性别”与“在线上买不买生鲜食品”之间无关,H_1:两变量之间有关 H0:“性别”与“在线上买不买生鲜食品”之间无关,H1:两变量之间有关 - 列出相关性表:相关性表的每列是每一种目标值,如患病和不患病、有效和无效、骰子取值123456等。每行是每种条件,分观察值和理论值。

- 计算 χ 2 \chi ^{2} χ2值。
χ 2 = ∑ ( O − E ) 2 E = ( 527 − 484 ) 2 484 + ( 72 − 115 ) 2 115 + ( 206 − 249 ) 2 249 + ( 102 − 59 ) 2 59 = 58.4 \chi ^{2}=\sum\frac{(O-E)^2 }{E}=\frac{(527-484)^2 }{484}+\frac{(72-115)^2 }{115}+\frac{(206-249)^2 }{249}+\frac{(102-59)^2 }{59}=58.4 χ2=∑E(O−E)2=484(527−484)2+115(72−115)2+249(206−249)2+59(102−59)2=58.4 - 确定自由度与理论 χ 2 \chi ^{2} χ2值。
d f = ( 行 数 − 1 ) ( 列 数 − 1 ) = ( 2 − 1 ) ( 2 − 1 ) = 1 df=(行数-1)(列数-1)=(2-1)(2-1)=1 df=(行数−1)(列数−1)=(2−1)(2−1)=1
拒 绝 域 : χ α 2 ( d f ) = χ 0.1 2 ( 1 ) = 2.71 拒绝域:\chi_\alpha^2(df)=\chi_{0.1}^2(1)=2.71 拒绝域:χα2(df)=χ0.12(1)=2.71 - 比较计算所得 χ 2 \chi ^{2} χ2值与理论 χ 2 \chi ^{2} χ2值。
χ 2 = 58.4 > χ 0.1 2 ( 1 ) = 2.71 \chi ^2=58.4>\chi_{0.1}^2(1)=2.71 χ2=58.4>χ0.12(1)=2.71
决策:在 α = 0.1 α=0.1 α=0.1的水平上拒绝 H 0 H_0 H0 ;
结论:认为“性别”与“在线上买不买生鲜食品”显著相关。
