Extreme Extension 思维，dp

题意：

• 给一数组a，可对其中$a_i$进行如下操作：将$a_i$拆成两数之和，然后代替$a_i$加入数组中。设一个数组的 $extreme$ $value$ 指的是：使得数组单调不下降的最小操作次数。据此，求a数组的所有子数组的 $extreme$ $value$ 之和

思路：

• 先考虑一个数组，显然，将末尾元素拆分是没有意义的，且会使答案增大。而对于中间元素，例如 $...[17],5,10,23,...$ ，如果它违反了单调不下降的规则，就必须进行拆分，可以有多种拆法，但使得其中最小元素尽可能大，是最优的拆法。例如，拆成$(4,4,4,5)$比$(3,3,3,3,5)$更好，因为这可能减少前面需要的操作数量，因此，相当于让拆分成的元素尽可能接近，且数量尽可能少，又要让其中最大的小于$a_{i+1}$，那么，对于当前的数$a_i$和下一个数$a_{i+1}<a_i$，我们应当拆分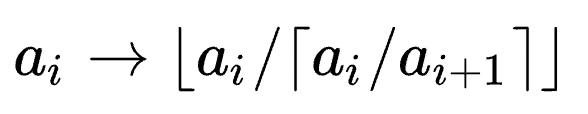，例如这里17应当分为$\lceil 17/5\rceil =4$个数，所以最小数是$\lfloor 17/4\rfloor =4$。显然，如果$a_i$比$a_{i+1}$小，则认为我们将它“拆分成一个数”
• 这样扫一遍下来，以$O(n)$解决了求解单个数组的问题，但是，子数组的数量是$n^2$数量级，不能全部这样求解
• 考虑$d{p}_{i,x}$是第$i$个数被拆分成最小元素为$x$的若干个数，并且以$x$开头的非递减数列的数量。有$d{p}_{i-1,y}$ += $d{p}_{i,x}$，因此可以转化。
• 一个数$n$拆分为最小元素$x$ $\in$ { $n$,$\lfloor n/2\rfloor$,$\lfloor n/3\rfloor$,…,$1$}，这个集合中元素个数不是n个，而是$O(n^{1/2})$数量级的，这一点在整除分块的技巧中也有使用。
• 最终我们根据$dp$数组统计答案。对于$dpi+1,x$，它对答案的贡献是$i\ast d{p}_{i+1,x}\ast (\lceil a_i/a_{i+1}\rceil -1)$，这是因为有$i\ast d{p}_{i+1,x}$个数列，每个数列对$a_i$执行这样的拆分

#include <iostream>
#include <unordered_map>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;
const ll mod = 998244353;

int a[N];

int main()
{
    
    
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    
    int _;
    cin >> _;
    
    while (_ -- )
    {
    
    
        int n;
        cin >> n;
        for (int i = 1; i <= n; i ++ ) cin >> a[i];
        
        unordered_map<int, int> dp[2];
        
        ll ans = 0;
        for (int i = n; i >= 1; i -- )
        {
    
    
            dp[1][a[i]] = 1;
            for (auto it : dp[0])
            {
    
    
                int t = ceil(a[i] * 1.0 / it.first);
                dp[1][a[i] / t] += it.second;
                ans += ((ll)i * it.second) * (t - 1);
            }
            ans %= mod;
            swap(dp[0], dp[1]);
            dp[1].clear();
        }
        
        cout << ans << endl;
    }
    
    return 0;
}