一、特征分解概述
在数学上,本征分解是线性代数的一部分,我们用它来将矩阵分解为其规范形式。在使用特征分解进行因式分解后,我们根据其特征向量和特征值来表示矩阵。需要说明的是,只能使用特征分解来分解方阵。
对应于一个二次方程的矩阵的特征分解可以用来找到这个函数的最小值和最大值。
特征分解是矩阵分解的一种形式。分解矩阵意味着我们要找到一个等于初始矩阵的矩阵乘积。在特征分解的情况下,我们将初始矩阵分解为其特征向量和特征值的乘积。
首先,需要了解矩阵和线性变换之间的联系。以及什么是特征向量和特征值?
机器学习笔记 - 特征向量和特征值_bashendixie5的博客-CSDN博客![]() https://blog.csdn.net/bashendixie5/article/details/124243609
https://blog.csdn.net/bashendixie5/article/details/124243609
二、特征分解公式
现在我们已经了解了特征向量和特征值是什么,我们可以看到如何使用它来分解矩阵。
1、矩阵![]() 的所有特征向量都可以放到一个矩阵中
的所有特征向量都可以放到一个矩阵中![]() ,每一列对应于每个特征向量(就像在 np.linalg.eig(A) 返回的第二个数组中一样)。
,每一列对应于每个特征向量(就像在 np.linalg.eig(A) 返回的第二个数组中一样)。
2、第一列特征值λ=6,第二列特征值λ=2。
3、特征分解公式:![]()
4、其中![]() 是一个包含了所有特征值的对角矩阵
是一个包含了所有特征值的对角矩阵 。
。
5、![]() ,我们根据
,我们根据![]() 和np.linalg.inv(V)函数进行计算
和np.linalg.inv(V)函数进行计算![]() 。
。
6、带入方程
7、计算 ,然后得到
,然后得到 。
。
使用python验证,将证实了我们之前的计算。
lambdas = np.diag([6, 2])
A = V.dot(lambdas).dot(V_inv)
print(A)三、用于实对称矩阵
在实对称矩阵的情况下,特征分解可以表示为![]() 其中Q是以特征向量为列的矩阵,Λ 是diag(λ)。
其中Q是以特征向量为列的矩阵,Λ 是diag(λ)。
证明如下:
1、有对称矩阵如下
2、有特征向量如下![]()
3、特征值矩阵如下
4、 并
并![]()
5、
python代码验证
A = np.array([[6, 2], [2, 3]])
eigVals, eigVecs = np.linalg.eig(A)
eigVals = np.diag(eigVals)
print(eigVecs.dot(eigVals).dot(eigVecs.T))还可以使用TensorFlow库使用特征分解
import numpy as np
import tensorflow as tf
data = np.array([[6.0, 2.0], [2.0, 3.0]])
values, vectors = tf.linalg.eigh(data)
print('eigenvector :',vectors)
print('eigenvalues :',values)输出如下
eigenvector : tf.Tensor(
[[ 0.4472136 -0.89442719]
[-0.89442719 -0.4472136 ]], shape=(2, 2), dtype=float64)
eigenvalues : tf.Tensor([2. 7.], shape=(2,), dtype=float64)四、用于二次方程矩阵
特征分解可用于优化二次函数。当X取特征向量的值,F(×)取其对应特征值的值。
1、设有二次方程![]()
2、矩阵形式
3、即 并且
并且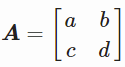 ,称它们为矩阵形式。 这种形式对于二次方程很有用,比如约束优化。
,称它们为矩阵形式。 这种形式对于二次方程很有用,比如约束优化。
1、例1
设有 并且
并且 ,可以给出
,可以给出
假如 ,则可以给出
,则可以给出
2、例2
设有 并且
并且 ,带入公式
,带入公式
因此,我们的二次方程是:![]()
五、变量的变化
1、二次形式
1、设有如下一个二次方程![]()
2、其中 并且
并且
3、A得特征向量为
4、为了简化,我们可以将这些值替换为:
5、所以特征向量为 和
和
6、变量的变化会导致
7、所以
8、带入原方程

2、主轴定理
使用主轴定理也会得到上一个例子的结果。
1、我们有如下函数![]()
2、我们希望是这样线性形式![]()
3、为了找到P,我们先把带入1内,得到
4、我们可知存在一个包含A的特征向量的对角矩阵D,使得![]()
5、最终我们得到![]()
6、所有这些都意味着我们可以使用 D 来简化我们的二次方程并去除交叉项。 我们知道上一个例子A的特征值为: ![]()
7、最终可得 ,这种形式(没有交叉项)称为主轴形式。
,这种形式(没有交叉项)称为主轴形式。
六、用特征分解求 f(x)
当 x 是单位向量时,有一种方法可以用特征向量和特征值找到 f(x)。
1、![]()
2、通过Ax=λx可得,![]()
3、因为x是单位向量,![]() 并且
并且![]()
4、我们得到![]()
1、例1
1、![]()
2、 其中 并且
并且
3、特征向量![]() 和特征值
和特征值![]()
4、所以![]()
5、 
6、如果![]()
7、