课程来源:吴恩达 深度学习课程 《改善神经网络》
笔记整理:王小草
时间:2018年5月29日
1.超参数调试
1.1 超参数
至此,神经网络基本的超参数已经遇到了这些(按重要性分类):
第一重要:
learning rate
第二重要:
momentum中的β
learning rate decay
mini-batch size
第三重要:
layers’ number
hidden unit number
不太重要,一般给定不调整:
Adam中的β1(=0.9), β2(=0.999), ε(10^-8)
1.2 网格搜索最优超参数
在传统的机器学习中一般会使用网格搜索(grid search)寻找最优的参数。
(1)一般做法:使用网格
假设需要调试两个参数,各自设5个值,那就是25个组合。对每个组合都进行模型训练,选择出使得模型表现最好的参数组合。
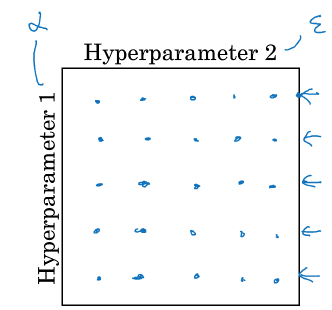
若使用参数learning rate(α)和 adam中的ε,会发现无论ε取何值,对model performance没有啥影响,而有影响的是α,即25次搜索中只有5次有用。因此这样的参数组合搜索方式其实是浪费了时间与资源的,我们更希望对有意向的参数去做更多搜索,从而尽可能找到优秀的参数值。
(2)改进做法:使用随机值
对2个超参数进行随机算则25个组合,同样也用25中情况,但因为是随机的,这25种情况中25个α值都不同,选择更多,则更有利于找到最优值。
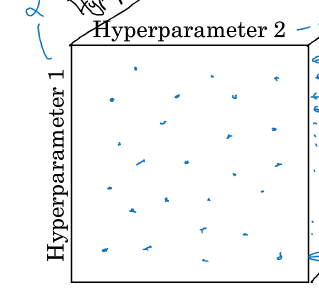
并且,在实际中,往往有很多超参数,且又不知道哪个更好,因此使用random的方式可探究更多重要的超参数的值。
(3)更改进做法:choose to fine
step1:同(2),随机选择参数组合,进行模型评估。
step2:发现某一块区域的组合普遍优秀,对该区域进行更精细化的随机搜索。
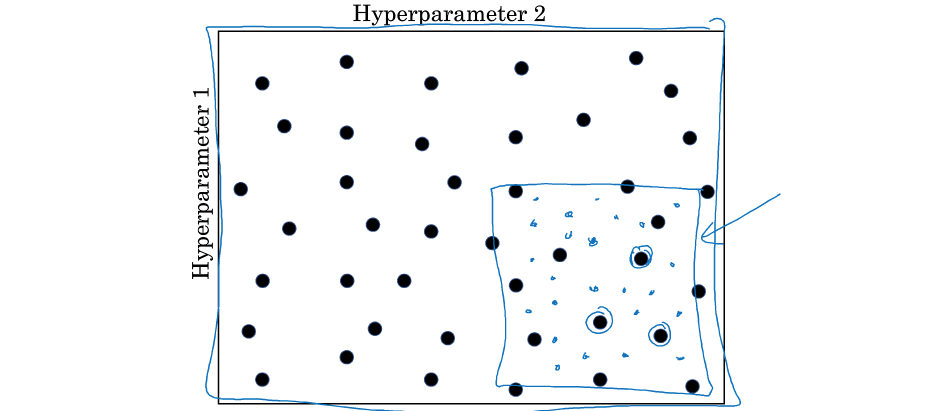
1.3 为超参数选择合适的范围
上一节的随机取值并不是在有效的范围内随机均匀取值,而是选择适合的scale来探索超参数。
对于神经网络的层数,神经元数目等超参数,在合适的范围内进行随机均匀取值(即每个值取到的概率相同)是合理的。但是对于某些超参这显然不和合理。
(1)比如学习率
假设你觉得学习率的范围应该是0.0001到1之间,如果随机均匀分布,那么选取到0.0001到0.1之间的概率只有10%,而0.1到1之间的概率有90%。但根据经验,学习率大部分情况下在0.1以下可能会更好,因此我们用了90%的资源去在10%的概率中寻找最优值。
因此要阔刀0.0001到0.1之间的概率。将0.0001到1之间平分四段,以为0.0001,0.001, 0.01, 0.1分割,如此,就有90%的概率会取到0.0001到0.1之间的数值了。
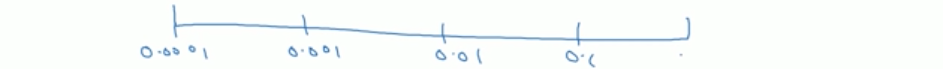
在python中可以如下实现:
r = -4 * np.random.rand()
α = 10^r(2)比如adam中的β
参数需要在0.9-0.999之间,因此做法是,对1-β在0.1到0.001之间平分
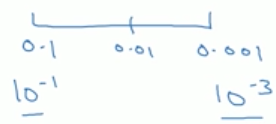
因此:
r = -3 * np.random.rand()
1-β = 10^r
β = 1-10^rβ的值会分布在:
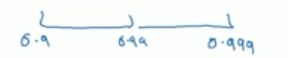
为何要如上分区呢?
因为当β越接近于1时,β会对细微的变化变得很敏感,因此在整个sampling的过程中,需要更加密集地取值在接近1的区间内。
1.4 超参数训练实践
对于超参数的训练,有两个流派
(1)babysitting one model
在没有足够的计算资源的情况下,一个人照看一个Model,并且观察每天的训练情况。并且不断根据模型的表现去调整参数,比如day1,day2调整学习率day3加上momentum…
(2)training many model parallel
在资源富足的情况下,用不用的参数组合训练不同的模型,最后选择效果最好的。
2.Batch Norm
Batch Normlization是由Sergey loffe和Christian Szededy两位研究者创造的。
Batch Normlization的优点:
使得参数搜索问题变得容易;
使得深层神经网络更容易训练。
2.1 正则化网络中的激活函数
对于输入层我们已经知道,输入的normalization之后可以有利于梯度下降中求解第一个隐层的最优参数。
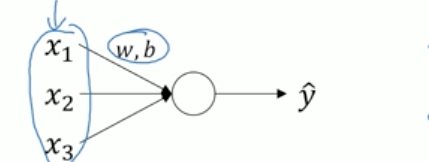
对于激活函数的normalization同理,激活函数的输出值其实就是下一个神经网络的输入值,因此normalization之后,能有助于更好的求下一层的参数。操作也是同理,使得所有值都减去均值后除以方差,变成均值为0,方差为1的标准正态分布。
对于激活函数的归一化,有两种说法,有些论文中是对激活函数的中间值z[l]进行nomalization,有些是对激活函数的最终输出a[l]进行nomalization,此处我们使用前者。
在某一个隐层,有:z(1),z(2),…,z(m)
于是nomalization的计算如下:
(1)计算均值:
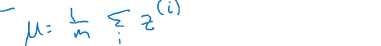
(2)计算方差
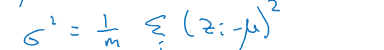
(3)计算标准化后的值
分母中加了一个ε,是为了防止σ为0的时候分母为0公式无效。
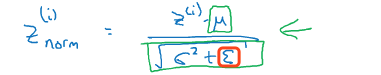
(4)计算最终值
由于正太标准化之后,每一隐藏层的分布都变成了(0,1)正态分布,但其实我们希望层都有不同的分布学习到不同的东西,因此要引入γ和β两个参数来改变分布:

γ和β也属于参数,需要像w,b一样使用梯度下降法去求得。
如果:
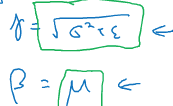
则:
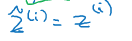
2.2 将batch norm拟合进神经网络
对整个神经网络的隐藏层进行normalization.如下神经网络:
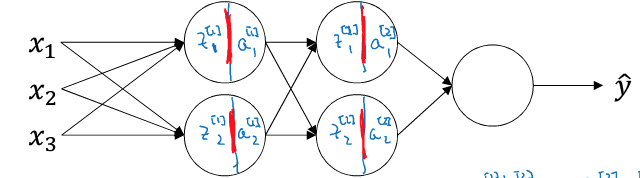
若对所有隐藏层进行normalization,则前向计算如下:
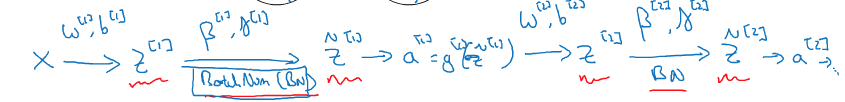
反向传播求梯度与的过程与之前完全一样,只是现在多了两个要更新的参数:γ和β
一般情况下,batch norm与nimi-batch是一起使用的。
batch 1: X{1}
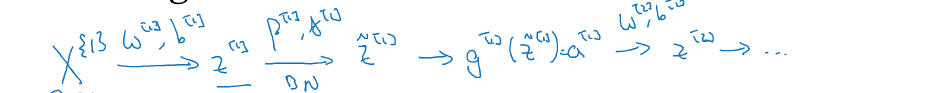
batch 2: X{2}

batch 3: X{3}
……
涉及的参数有W,b,β,γ
因为nomalization的过程,均值为0的过程会抵消所有常数项,因此b参数可以被删除,或者将b设置为0.
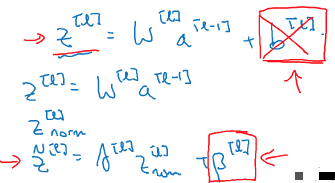
2.3 batch norm为何奏效
2.3.1 优点1
与输入层一样,对隐藏层的normalization使得参数的梯度在同一范围内,也可以加速梯度下降的速度。但只是batch norm优点的冰山一角呢。
2.3.2 优点2
batch norm还可以使权重比你的网络更滞后或更深层,比如第10层的权重更能经受得住变化。
举一个例子:
假设你搞了个神经网络去训练黑白猫的图片,然后你再把该网络应用在识别有色猫上,那么效果并不好。因为你的训练集的黑白猫的正负样本分布可能如下:
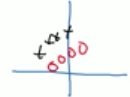
而彩色猫的正负样本可能如下:
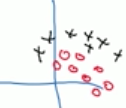
显然他们的分布不同,自然无法共享分类器了。
以上问题,是由“covariate shift”导致的。
那么covariate shift具体是如何影响神经网络的呢?
假设有一个这样的神经网络:
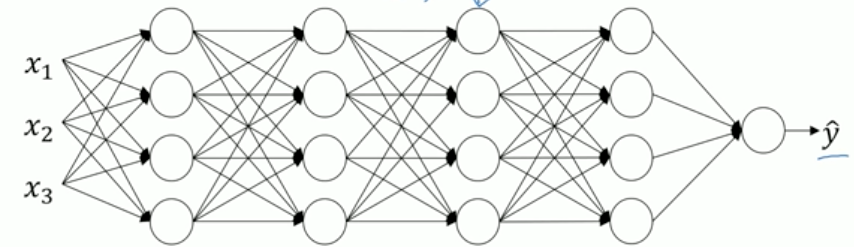
现在我们来研究它的第3层的学习过程,现在已经学到了第三层的权重是w[3],b[3];第三层的输入是第二层的输出a[2],它在学习中要使a[2]与权重w[3],b[3]计算后能使得预测值y^与y尽量接近。
如果前面的输入a[2]是固定不变的,那啥事木有,因为输入固定,只需要去专心学习参数就行。但是!实际上前一层的a[2]是受该层的w[2],b[2]影响的,而w[2],b[2]是受前一层的a[1]影响的,而a[1]是受该层的权重w[1],b[1]影响的。在梯度下降中,更新了w[1],b[1]的权重,前面的分布改变了,那么使得后面的每一步参数与输出都改变了分布(这就是covariate shift)。对于第三层来说,a[2]并不是固定的,于是也影响了w[3],b[3]的正确学习。
那么batch norm又是如何解决covariate shift问题的呢?
batch norm可以确保当前的参数更新时,仍然使得z[i]的方差与均值保持不变,即限制了参数更新而印象数值分布的程度,减轻了前层参数与后层参数作用之间的联系。使得each layer of network to learn by itself。从而也加快了整个神经网络的学习与训练速度。
2.3.3 优点3
batch norm还有一点点正则化的效果。
batch norm一般和Mini-batch一起使用。因此计算均值与方差其实是在每个Min-batch上计算,并不一定是全局的均值与方差,因此有误差,带来了一点噪音。
因此与dropout类似,batch norm为神经网络的每一层激活函数增添一点噪音。但是batch norm的正则强度较小,因此仍可以将batch norm与dropout一起使用。
Mini-batch的size越大,则产生的正则越小。
2.4 测试时的batch norm
在test中需要单独估算均值与方差。
设有n个mini-batch,每个batch在训练中都已经计算出了各自的均值μ与σ:
X{1}: μ1, σ1
X{2}: μ2, σ2
…
X{n}: μn, σn
根据以上值,使用指数加权移动平均法计算出新的μ, σ
然后将新的μ, σ进行z的normalization过程:
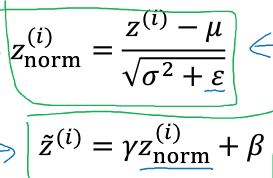
3.多分类–softmax
3.1 softmax 回归
在多分类问题中需要使用softMax regression.
假设你要识别3种小动物,分别标记为1,2,3若不属于任何一种则标记为0,总共4个类别。

符号表示:
C:类别的数目
n[l]:第l层的神经元个数(则输出层的n[l]=C)
输出层的每个神经元的值即代表中每个类别的概率,因此预测值y^是一个(4,1)的向量,且向量值相加为1。
要实现上面的输出,则需要一个softmax层和一个outout层合作。
4分类的结构如下:
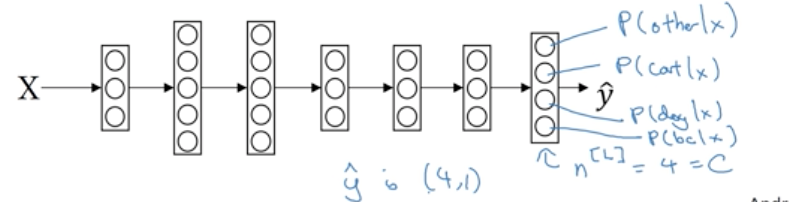
softmax层一般都放在神经网络的最后一层,计算过程如下:
step1:计算z
和其他隐层一样,先将参数w,b进行现行计算得到z(Z是一个(4,1)的向量)

step2:过一个softmax激活函数
先计算一个临时值t(t也是一个(4,1)的向量)

然后计算最终的激活值a(a也是一个(4,1)的向量),该过程将t归一化到0-1之间的概率。

例子:
step1:计算z
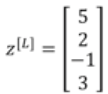
step2:过一个softmax激活函数
计算t:

计算a(g[l]=a[l]):
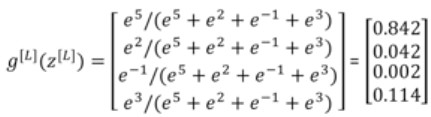
3.2 训练softmax分类器
softmax regression是对logistic regression在多分类上的推广,
当C=2时,softmax regression = logistic regression。
进入正轨。
一张猫猫的图片的真实值y为:
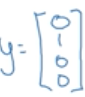
经过前向计算,得到预测值y^为:
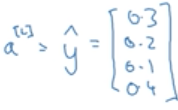
真实值为1的位置预测值只有0.2的概率,不是最大概率,因此预测得并不好。
损失函数(单样本)
如何计算损失呢,损失函数如下:

根据以上案例,y只在y2为1,其他部分为0,因此损失函数为:
L(y^,y) = -y2logy2^
因为y2 = 1
L(y^,y) = -logy2^
可见,要使得损失L越小,则y2的值需要越大,若y2=1则损失为0.
代价函数(总体样本)
以上是单样本的损失,那么所有样本的损失的均值,就是代价函数的值:
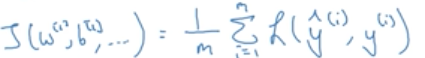
根据代价函数,可以利用梯度下降法求解参数最优值。
利用矩阵的形式表示Y, Y^
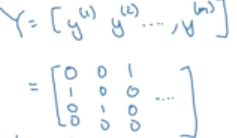
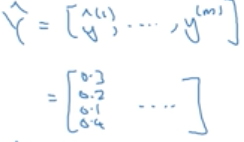
每一列都表示一个样本,维度都是(4,m)。m是样本的个数,4是类别的个数。
softmax层如何实现梯度下降
与logistic不同的是只是激活函数的计算不一样了,因此只是softmac层的z的梯度有变:

dz的维度是(4,1)
4.深度学习框架
4.1 深度学习有哪些常用的框架

选择框架参考的因素:
(1)编程友好
(2)运行速度快
(3)开源
4.2 tensorflow初步使用
tensorflow的使用教程另开篇章