最近在LeetCode的每日一题和实验中接连遇到凸包问题，因为之前从来没写过，于是写这篇博客记录一下，内容部分参考每日一题的官方题解和算法导论。算法的具体描述以及代码实现多为个人理解，如有谬误还请指出。

问题定义

点集 $Q$ 的凸包(Convex hull)是一个最小的凸多边形 $P$ ，满足 $Q$ 中的每个点都在 $P$ 的边界上或者在 $P$ 的内部。现给定一个点集，求解其凸包（即构成凸包的点集）。

下图给出了 $p_0...p_{12}$ 的闭包：
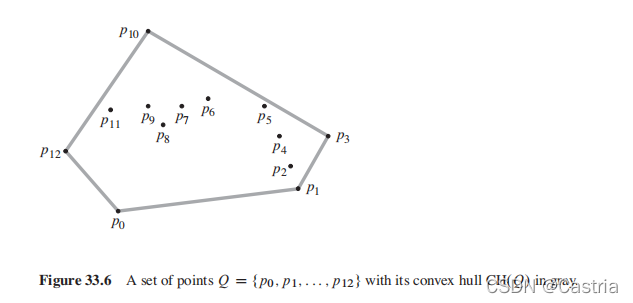
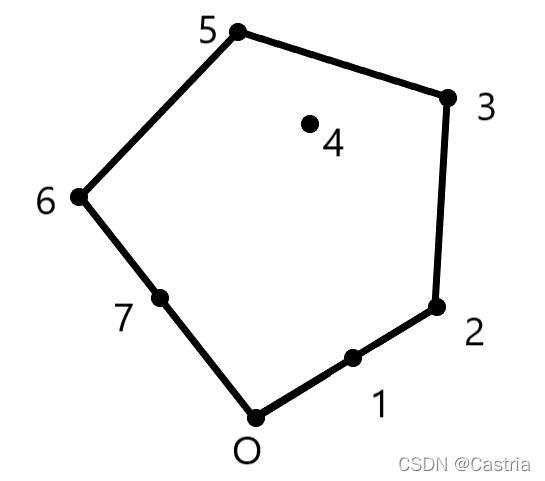
在这里插入图片描述

Graham扫描法

Graham扫描法由Graham在1972年提出，它可以以 $O (n l o g n)$ 时间复杂度求解凸包问题，其中 $n$ 为点集大小。以下是算法的伪代码：

GRAHAM-SCAN(Q)

令p_0为Q中具有最小纵坐标的点（当存在多个时，选取横坐标最小的点）;
令<p_1,p_2,...,p_m>为Q中剩下的点，以p_0为极点对这些点按照极角逆时针排序（若两点极角相同，仅保留距离最大的那个）;
if m < 2
	return "凸包为空"
else
	令S为空栈
	PUSH(p0, S)
	PUSH(p1, S)
	PUSH(p2, S)
	for i = 3 to m
	while NEXT-TO-TOP(S),TOP(S)和p_i形成非左移动
		POP(S)
	PUSH(p_i, S)
	return S

下面分别对算法各部分进行说明。

确定极点

这一步是为了确定后面所需的基准点。由于纵坐标最小的点一定在凸包上，因此它一定可以作为基准点。至于选择横坐标最小的点的要求放到后面解释。
Java代码：

//函数原型
public static Set<Point> convexHull(Set<Point> points) {
    
    }

int index = -1;
for(Point p: points) {
    
    
	pointList.add(p);
    if(index == -1) index = 0;
    else {
    
    
        Point miny = pointList.get(index);
        if (p.y() < miny.y() || (p.y() == miny.y() && p.x() < miny.x())) {
    
    
                index = pointList.size() - 1;
        }
    }
}

按极角排序

为了将点按照极角排序，需要叉乘运算辅助。在平面上，两个向量的叉乘定义为 $\vec a \times \vec b=absin\theta$ (这里不考虑结果的方向),其中 $\theta$ 是 $\vec a$ 转向 $\vec b$ 的不超过 $180\degree$ 的角度。当 $\vec a$ 顺时针转向 $\vec b$ ， $\theta>0$ ;否则 $\theta<0.$ 若 $\vec a=(x_1,y_1),\vec b=(x_2,y_2),$ 有 $\vec a \times \vec b=x_1y_2-x_2y_1.$ 因此，为了确定两个点 $A, B$ 以 $O$ 为极点的顺序，可以求叉乘 $\overrightarrow{OA} \times \overrightarrow{OB},$ 若
$(1)\overrightarrow{OA}$ 顺时针转向 $\overrightarrow{OB},$ 此时有 $\theta>0,$ 叉乘值大于 $0$ , $A$ 排在 $B$ 的前面；
$(2)$ 否则，当 $\theta<0$ , $A$ 排在 $B$ 的后面。
$(3)$ 当 $O, A, B$ 在一条线上，伪代码指出我们应该去掉距离 $O$ 更近的那个，但排序时删除点实现起来很麻烦，我们在这里将它们按距离排序：更近的排在前面。
代码实现：

Point base = pointList.get(index);//极点

pointList.sort(new Comparator<Point>() {
    
    
    @Override
    public int compare(Point A, Point B) {
    
    
    		//把极点放到最前面
            if(A.x() == base.x() && A.y() == base.y()) return -1;
            if(B.x() == base.x() && B.y() == base.y()) return 1;
			
			//逻辑同上文
            double crossVal = cross(base, A, B);
            if(crossVal == 0) {
    
    
                if(dist(base, A) < dist(base, B)) return -1;
                return 1;
            }
            if(crossVal > 0) return -1;
            return 1;
        }
});

前面提到，伪代码告诉我们应该去掉相同极角的点中距离更小的，但是我们没有去掉。因此我们需要对下面的情况进行修正：
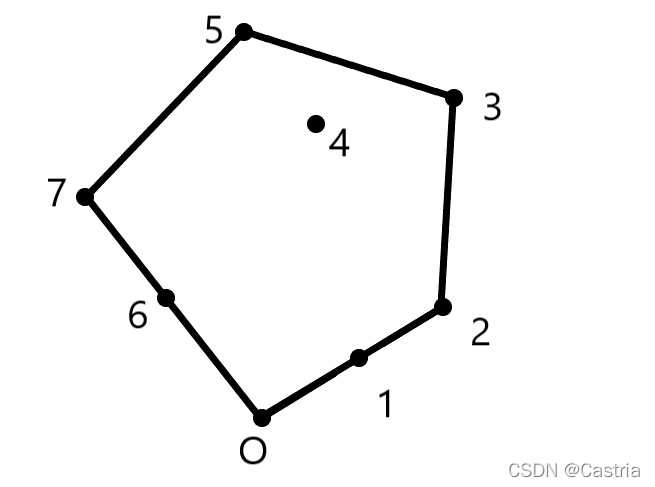
在这里插入图片描述
在求凸包的过程中，我们从逆时针地考察每个点，最后围成一个凸包，因此按照直觉，我们应该由近到远，再由远及近地考察。按照这个原则，图中1，2点的位置是正确的；但6，7点的位置反过来了。（若按照伪代码中的算法，1、6被去掉了，不会影响凸包的计算）因此，我们把极角最大的共线的这些点反转一下顺序（在图中即把6、7反过来）。此外，将这些点中最近的那些点去掉（否则也会有问题，放到后面解释）：

int ptr = pointList.size() - 1;

//确定最后共线的点，最后[ptr+1,size-1]就是这些点
while(ptr >= 0 && cross(base, pointList.get(pointList.size() - 1), pointList.get(ptr)) == 0) ptr--;
//将它们反转
for(int p = ptr + 1, q = pointList.size() - 1; p < q; p++, q--) {
    
    
    swap(pointList, p, q);
}
//移除最近的点，只剩下ptr+2个([0,ptr+1]共ptr+2个点)
while(pointList.size() > ptr + 2) pointList.remove(pointList.size() - 1);

确定凸包

图片模拟了求解的部分过程
$(1)$ 对于 $n\leq3$ 的情况，可以直接返回。（不考虑共线等情况）
$(2)$ 否则，初始化空栈并将最前面的两个点放入栈中。对于接下来的每个点 $B$ ，设当前栈顶点为 $A,$ 栈内接下来一个点为 $O$ ,若 $\overrightarrow{OA}$ 通过顺时针转动 $\theta>0$ 可以指向 $\overrightarrow{OB}$ 的方向，那么直接将 $B$ 入栈；否则，称此时形成非左移动，将 $A$ 出栈，重复操作直到栈中元素个数 $< 2$ 或形成左移。再将 $B$ 入栈。

注意我们还是没有完全按照伪代码中执行（初始将3个点放入栈中），考虑上面那张图：
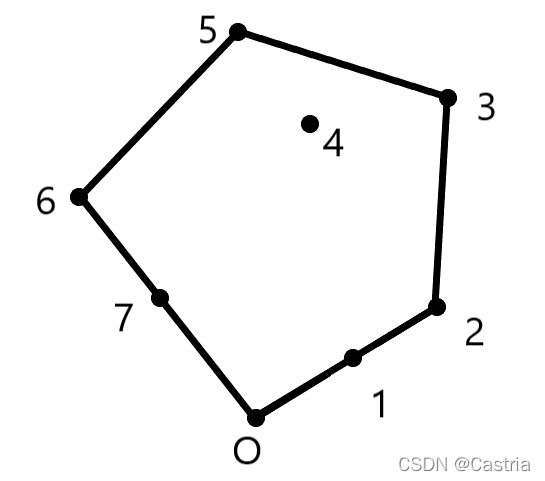
在这里插入图片描述

若一开始就将 $O, 1, 2$ 放入栈中，在考察点 $3$ 后将其直接入栈，点 $1$ 就留在了栈中，导致所求点集不是最小凸包（当然，若不要求最小，这条限制无所谓）。而如果一开始只放入两个点，在考察 $2$ 时由于形成非左移动（共线当然也算非"左"），就将 $1$ 出栈。
代码实现：

for(int i = 2; i < pointList.size(); i++) {
    
    
    while(S.size() >= 2) {
    
    
    	//取值并出栈
        Point top = S.pop();
        //只取值不出栈
        Point nextTop = S.peek();
        //满足条件，将多pop的放回去并break
        if(cross(nextTop, top, pointList.get(i)) > 0) {
    
    
            S.push(top);
            break;
        }
    }
    S.push(pointList.get(i));
}

return new HashSet<Point>(S);//返回

最后，解释一下：
（1）为什么极点要选择横坐标最小的点；
（2）为什么需要将最后几个共线的点去掉最近的。
对于（1），考虑如下点集：
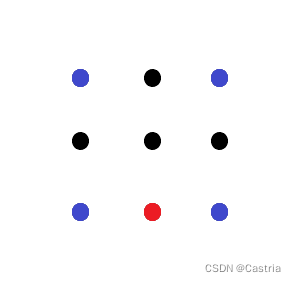
在这里插入图片描述
若将红点选作极点，最后选出的凸包点集是红点加上四个蓝点；然而这不是最小的凸包。纵坐标相同时按横坐标排序保证了选择左下角的蓝点作为极点，求出的凸包是最小的。
对于（2），

还是上面那张图：若不去掉7，最后在考察7时，按照上面逻辑判断，点5、6构成的向量可以通过向左旋转指向点7，那么会将7放入栈中，导致闭包不是最小。去掉最后几个点中最近的可以避免这一点。

下面的一张gif模拟了Graham扫描法的求解过程：（图源：Wikipedia Graham Scan词条）
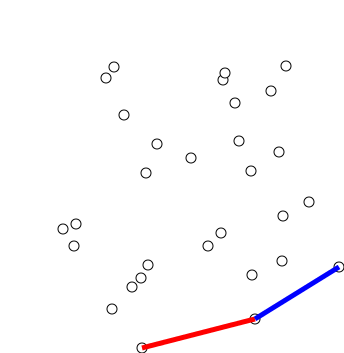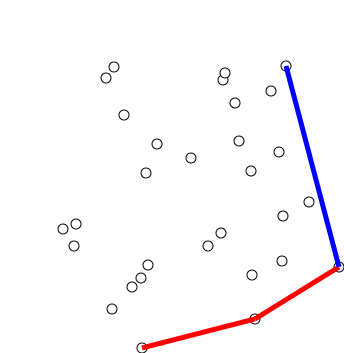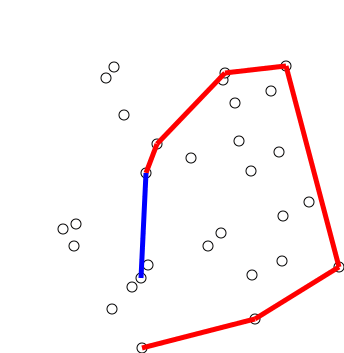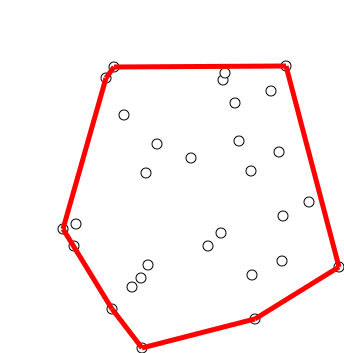
在这里插入图片描述

时间复杂度

对于排序后的每个点，它至多出入栈一次，因此这部分时间复杂度为 $O (n)$ ；因此，程序的复杂度由排序的 $O (n l o g n)$ 决定。

完整代码（Java）

private static double dist(Point A, Point B) {
    
    
    double deltaX = B.x() - A.x();
    double deltaY = B.y() - A.y();
    return Math.sqrt(deltaX * deltaX + deltaY * deltaY);
}
private static double cross(Point O, Point A, Point B) {
    
    
    return (A.x() - O.x()) * (B.y() - O.y()) - (A.y() - O.y()) * (B.x() - O.x());
}
public static Set<Point> convexHull(Set<Point> points) {
    
    
    if(points.size() <= 3) return points;
    ArrayList<Point> pointList = new ArrayList<Point>();

    int index = -1;
    for(Point p: points) {
    
    
        pointList.add(p);
        if(index == -1) index = 0;
        else {
    
    
            Point miny = pointList.get(index);
            if (p.y() < miny.y() || (p.y() == miny.y() && p.x() < miny.x())) {
    
    
                index = pointList.size() - 1;
            }
        }
    }

    Point base = pointList.get(index);

    pointList.sort(new Comparator<Point>() {
    
    
        @Override
        public int compare(Point A, Point B) {
    
    
            if(A.x() == base.x() && A.y() == base.y()) return -1;
            if(B.x() == base.x() && B.y() == base.y()) return 1;

            double crossVal = cross(base, A, B);
            if(crossVal == 0) {
    
    
                if(dist(base, A) < dist(base, B)) return -1;
                return 1;
            }
            if(crossVal > 0) return -1;
            return 1;
        }
    });

    int ptr = pointList.size() - 1;
    while(ptr >= 0 && cross(base, pointList.get(pointList.size() - 1), pointList.get(ptr)) == 0) ptr--;
    for(int p = ptr + 1, q = pointList.size() - 1; p < q; p++, q--) {
    
    
        swap(pointList, p, q);
    }
    while(pointList.size() > ptr + 2) pointList.remove(pointList.size() - 1);

    Stack<Point> S = new Stack<Point>();

    S.push(pointList.get(0));
    S.push(pointList.get(1));

    for(int i = 2; i < pointList.size(); i++) {
    
    
        while(S.size() >= 2) {
    
    
            Point top = S.pop();
            Point nextTop = S.peek();
            if(cross(nextTop, top, pointList.get(i)) > 0) {
    
    
                S.push(top);
                break;
            }
        }
        S.push(pointList.get(i));
    }

    return new HashSet<Point>(S);
}

LeetCode 587.安装栅栏

这道题是2022.4.23的每日一题，它与上文介绍的不同点是，它要求的并非最小凸包，它要求所有在凸包边界上的点也应该被返回。大致思路与文章一致，但有两点需要注意：
（1）由于不要求最小凸包，可以按照算法导论中的伪代码，将前三个点初始地放入栈中；
（2）不需要去掉任何最后共线的那几个点。
（3）应当接受共线的点，即：当 $\overrightarrow{OA}\times\overrightarrow{OB}\ge0$ 时，将 $B$ 入栈。

C++代码(当时写的着急，代码比较丑，时空消耗也爆炸)：

class Solution {
    
    
public:
    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
    
    
        if(trees.size() <= 3) return trees;
        int base, basex = INT_MAX, basey = INT_MAX;
        for(int i = 0; i < trees.size(); i++) {
    
    
            if(trees[i][1] < basey || (trees[i][1] == basey && trees[i][0] < basex)) {
    
    
                base = i;
                basex = trees[i][0];
                basey = trees[i][1];
            }
        }

        auto dist = [](int ax, int ay, int bx, int by) {
    
    
            int deltaX = ax - bx;
            int deltaY = ay - by;
            return deltaX * deltaX + deltaY * deltaY;
        };
        auto cross = [](int ox, int oy, int ax, int ay, int bx, int by) {
    
    
            return (ax - ox) * (by - oy) - (ay - oy) * (bx - ox); 
        };

        //把极点放到最前面
        swap(trees[0], trees[base]);
        sort(trees.begin() + 1, trees.end(), [=](vector<int> a,vector<int> b){
    
    
            int v = cross(basex, basey, a[0], a[1], b[0], b[1]);
            if(!v) {
    
    
                return dist(basex, basey, a[0], a[1]) < dist(basex, basey, b[0], b[1]);
            }
            return v > 0;
        });

        int n = trees.size(), r = n - 1;
        while (r >= 0 && cross(trees[0][0], trees[0][1], trees[n - 1][0], trees[n - 1][1], trees[r][0], trees[r][1]) == 0) {
    
    
            r--;
        }
        for (int l = r + 1, h = n - 1; l < h; l++, h--) {
    
    
            swap(trees[l], trees[h]);
        }

        stack<vector<int>> S;
        S.push(trees[0]);
        S.push(trees[1]);
        S.push(trees[2]);
        for(int i = 3; i < trees.size(); i++) {
    
    
            while(true) {
    
    
                auto t = S.top();
                S.pop();
                auto nextt = S.top();
                if(cross(nextt[0], nextt[1], t[0], t[1], trees[i][0], trees[i][1]) >= 0) {
    
    
                    S.push(t);
                    break;
                }
            }
            S.push(trees[i]);
        }

        vector<vector<int>> v;
        while(!S.empty()) {
    
    
            v.push_back(S.top());
            S.pop();
        }
        return v;
    }
};

Graham扫描法求解二维凸包问题