本文主要是讨论卷积为什么满足交换率，而“相关”不满足，在此分享一下个人的想法，就不详细介绍卷积和相关的来龙去脉了，相关知识可以详见《数字图像处理（第4版）冈萨雷斯》
目录
一。卷积与相关
直接借用一下书上的原图
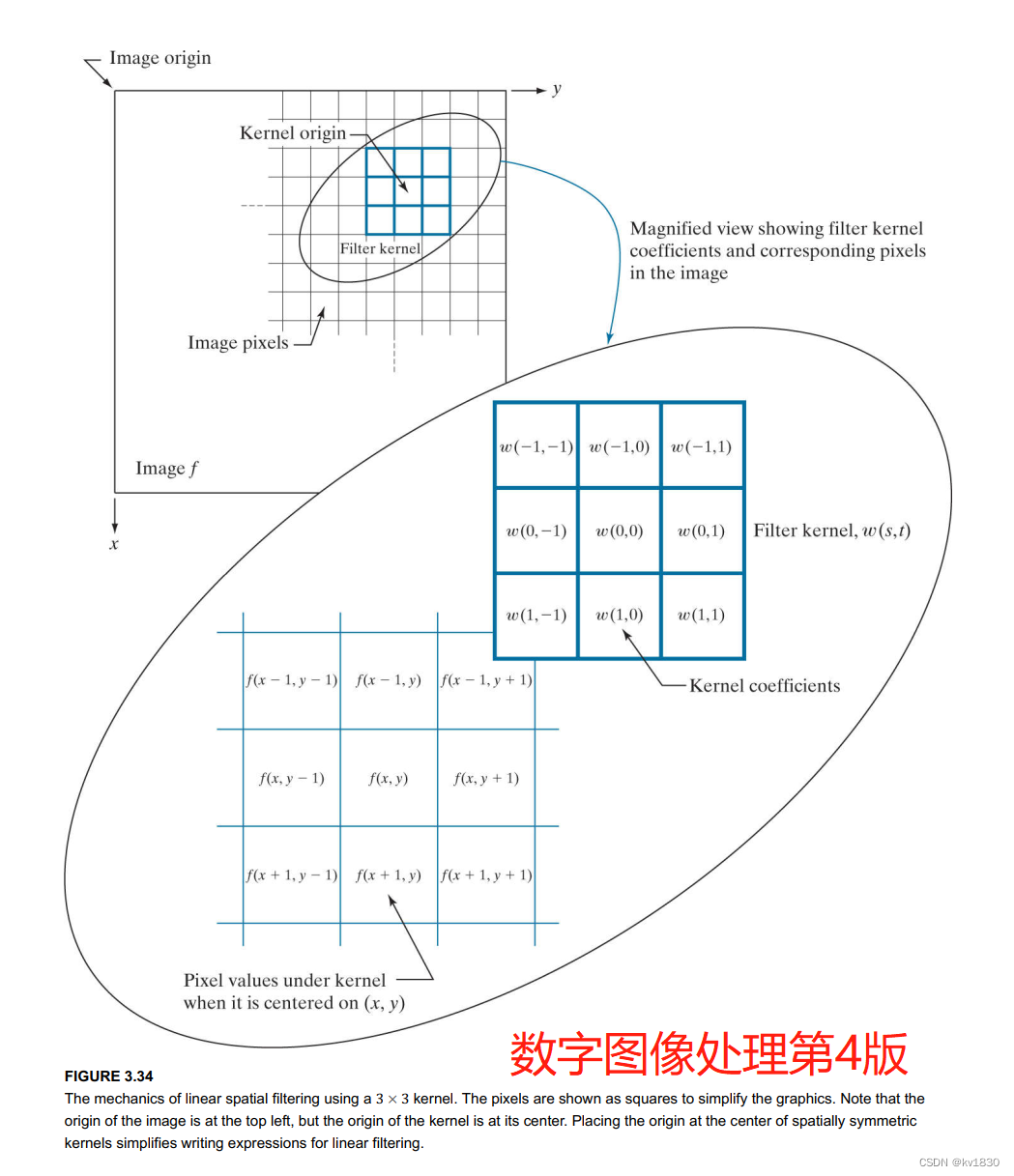
这是相关（公式截图仍然取自上书），这里用的是空心五角星：
这是卷积，这里用的是实心五角星：
也就说如果拿滤波器核直接依次跟图像上的点做运算，就是相关。如果把滤波器核按中心旋转180度再跟图像上的点做运算，就是卷积。这似乎跟我学深度学习的时候理解的卷积有点不一样，深度学习的卷积其实就是相关！
另外注意一下上面的写法，五角星前面的是滤波器核，后面的是图像（或者叫函数）
顺便提一下，opencv里的filter2D执行的是相关，而不是卷积，如果要执行卷积，得自己把卷积核旋转一下：
二。卷积为什么满足交换率，而“相关”不满足
可以看到上表的第二行，卷积是满足交换率的，而相关不满足，这是为什么呢？
我们先拿个实例来试一下，为了简化问题，我们先在一维空间来分析。
1.代码
先提供一下我所使用的代码，方便验证之用，注释已经说的很仔细了。要用到pytorch，numpy。为啥不用opencv的filter2D呢，因为它好像不支持完全相关/卷积，下面会说什么是完全相关/卷积
import torch
from torch import nn
def do_correlation(kernel, img, whole=False, do_conv=False):
"""
相关
:param kernel: 滤波器核
:param img: 图像
:param whole: 完全相关(完全卷积)，完全-True，不完全-False
:param do_conv: 卷积-True，相关-False
:return: 相关/卷积结果
"""
if whole:
p = kernel.shape[-1] - 1
else:
p = kernel.shape[-1] // 2
conv = nn.Conv1d(1, 1, 3, 1, padding=p, bias=False).eval()
if do_conv:
kernel = torch.from_numpy(kernel.numpy()[:, :, ::-1].copy())
conv.weight.data = kernel
return conv(img)
def do_convolution(kernel, img, whole=False):
"""
卷积
"""
return do_correlation(kernel, img, whole=whole, do_conv=True)
if __name__ == '__main__':
kernel = torch.tensor([[[1, 2, 3]]], dtype=torch.float32)
img = torch.tensor([[[4, 7, 6]]], dtype=torch.float32)
# kernel, img = img, kernel # 要交换滤波器核与图像，就用这一行
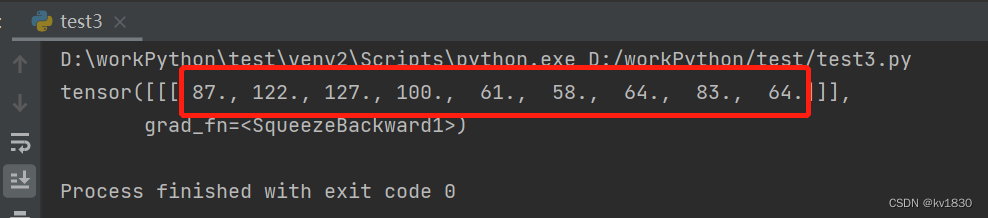
print(do_correlation(kernel, img, whole=False)) # 相关就用这个
# print(do_correlation(kernel, img, whole=False, do_conv=True)) # 要卷积就用这个
2.相关
(1)滤波器核：1 2 3， 图像：4 7 6，滤波器核中心点2对准图像左端的4，由左右向移动，直至移到图像右端的6。在两端处会有一部分核元素对不到图像元素，就会补0。
相关结果：29 36 19
注意，如果把1 2 3看作不动，那其实就是4 7 6由右向左移动，并且中心点7先对端图像右端的3，结束的时候对端图像左端的1，这个思维方式其实很重要！
(2)交换滤波器核与图像，滤波器核：4 7 6， 图像：1 2 3
相关结果：19 36 29
跟(1)中结果对比，正好反过来了。原因很简单，(1)中说了，把1 2 3看作不动，4 7 6就是由右至左。而现在呢，1 2 3本来就是不动的，4 7 6由左至右，那整个滤波过程不正好就是反过来的吗。
不过你可能会发现，这好像并不完全是返回来的情况啊，比如在(1)中，1 2 3在最左边的时候即：
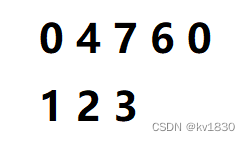
这个时候计算的滤波算式是：0*1+4*2+7*3
在(2)中，1 2 3在最左边的时候（也就是4 7 6在最右边的时候）即：
滤波算式是：4*2+7*3+6*0。这两算式其实不一样啊，但是它不一样的地方都是乘0的，这是没关系的。你完全可以这么去理解，滤波计算只作用于滤波器核与图像重叠的内容，不重叠的地方直接忽略，而代码里面为了统一计算，所以补了0，然后再乘0，那不就是没乘吗。
(3)复杂点的例子
你可能又会觉得，你举的这个例子是不是一个巧合呢？而且滤波器核、图像都只有3个元素，太简单了，那我们来个复杂点的。
滤波器核：1 9 5 7 3，图像：4 7 6 3 3 1 2 3 7
相关结果：
交换滤波器核与图像后的结果：
你看，不一样了！
先别急，我们再仔细看对比一下，你看这中间部分是不是仍然是反过来的。
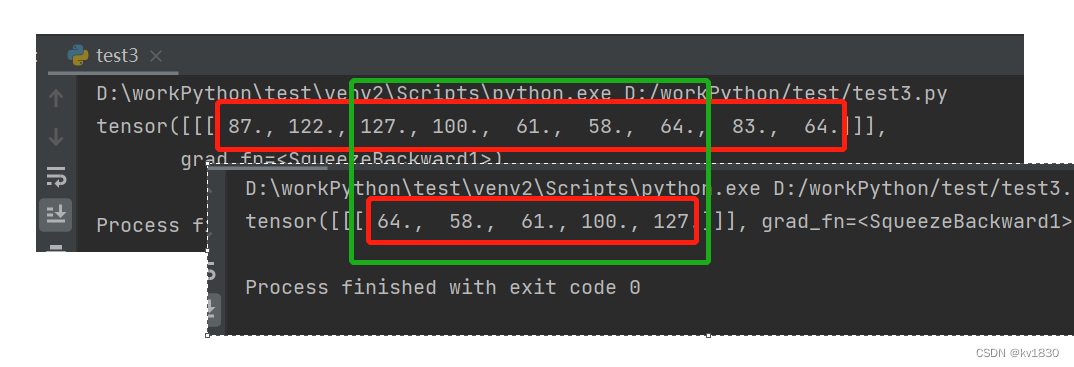
但是它们的长度不一样，所以导致整体结果不完全是反地来的而已。原因很简单，相关的结果长度跟图像长度是一样的，交换滤波器核与图像之后，图像长度变成5了，滤波器长度变成9，但它只能在图像上移动5步，那结果自然就变了。
而交换前，滤波器核能在图像上移动9步，这9步中间所对应的那5步跟交换后的5步仍然是反过来的，所以就出现了上面的结果。
那有没有办法让交换后的结果还是完全相反的呢？下面就引出了完全相关
3.完全相关
完全相关就是让滤波器核的每一个元素都能经过图像的每一个元素，就以上面那个复杂的例子来说
(1)滤波器核：1 9 5 7 3，图像：4 7 6 3 3 1 2 3 7
一开始就不是滤波器核中的的5去对图像左端的4了，而是3去对4。结束的时候是1去对7。这里就不把补0画上去了，你就认为我们只算重叠的，不重叠的不算就行，这样方便反过来思考。
完全相关结果：
既然滤波器核的每一个元素都能经过图像的每一个元素，那如果认为滤波器核不动，图像动，图像还是从右向左动，并且图像上的每一个元素都能经过滤波器核的每一个元素。为了方便思考，我把它画出来，就是下面这样：
(2)交换滤波器核与图像： 滤波器核：4 7 6 3 3 1 2 3 7，图像：1 9 5 7 3
比较一下上面两张图，滤波顺序是不是完全反过来的。
验证一下，完全相关结果如下，跟上面完全相反：
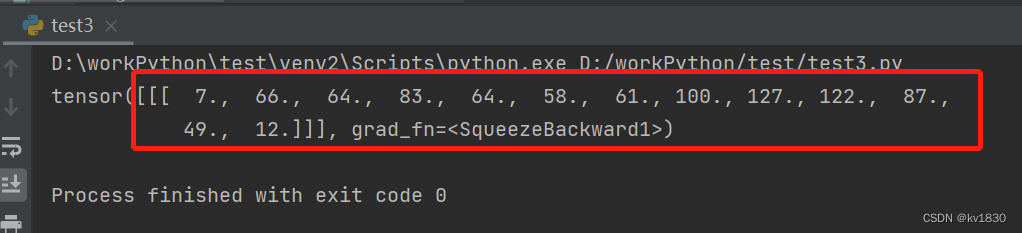
4.卷积
卷积跟相关的区别就是卷积会先把滤波器核绕着核心旋转180度（在1维层面来看就是倒过来），然后再去做滤波。
还是先用简单例子来演示卷积（注意，0我就都不补了）。
(1)滤波器核：1 2 3， 图像：4 7 6
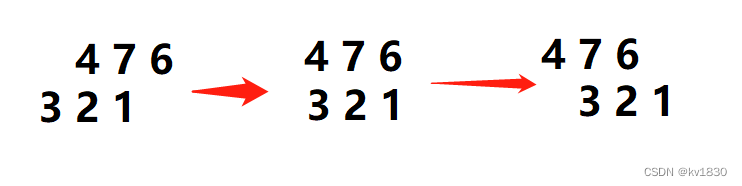
滤波过程如上图，注意滤波器核先旋转成3 2 1了，然后再进行滤波。
卷积结果：15 32 33
跟相关同理，我们也可以认为滤波核不动，图像4 7 6同，那么图像4 7 6 就是由右向左动。如下图
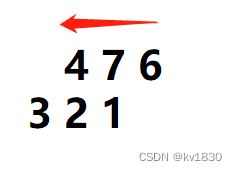--------图1
(2)交换滤波器核与图像，滤波器核：4 7 6， 图像：1 2 3
注意滤波器核仍然是要旋转再进行滤波的
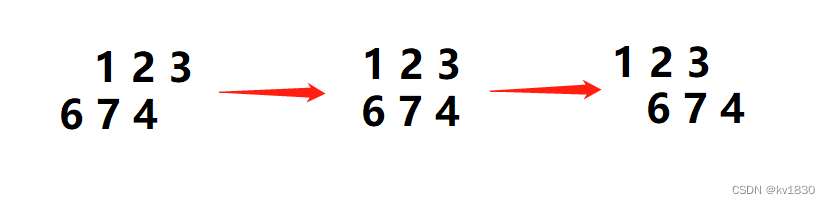
卷积结果：15 32 33，跟上面完全一样！
这里我们就把图像看作不动，滤波器核看作动了，如下图：
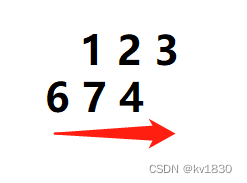---------图2
对比图1、图2，有没有发现，把图1照中心旋转180度，就能得出图2，连箭头都是带着转过来了。
这说明什么问题呢？说明它们的滤波过程其实是一模一样的！即每一时刻参与滤波的元素是一样的（当然没重叠的元素不算）！这也是卷积符合交换率的关键原因。
当然，如果图像的大小和滤波器不一样的话，那肯定就不会是完全相同了，这跟相关的情况是一样的，只有中间那部分才会是完全相同的，此时如果还想完全相同，就得用到完全卷积了。
5.完全卷积
完全卷积也是让滤波器核的每一个元素都能经过图像的每一个元素，还是用完全相关的那个复杂的例子来说
(1)滤波器核：1 9 5 7 3，图像：4 7 6 3 3 1 2 3 7
完全卷积结果：
(2)交换，滤波器核：4 7 6 3 3 1 2 3 7，图像：1 9 5 7 3
完全卷积结果：
跟交换前是一样的。原因就不再重复详述了，防止你是直接跳过来的，友情指路如下~~：
为什么一样，看4.卷积里面的分析
为什么完全一样，看3.完全相关里面的分析
6.二维场景
同理，二维的场景也是一样的，关键就是旋转180度，按照上述思想均都可进行验证，图比较复杂，我就不画了~~