为研究我国民航客运量的变化趋势及其成因，以民航客运量为因变量 $y$ （万人）,旅客运输量 $x_{1}$ （万人），入境游客 $x_{2}$ （万人），外国人入境游客 $x_{3}$ （万人），国内居民出境人数 $x_{4}$ （万人）和国内游客 $x_{5}$ （万人）为主要解释变量，建立多元线性回归模型并进行分析.（数据文件在文末）。

资料来源：中华人民共和国国家统计局年度数据，http://www.stats.gov.cn/tjsj/.

图1 民航客运量多因素分析数据

建立回归方程

根据ex2.3.csv的数据，建立 $y$ 关于 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 和 $x_{5}$ 的线性回归方程并对方程和回归系数进行显著性检验，R程序如下：

d2.3<-read.csv("ex2.3.csv",header = T) #将ex2.3.csv数据读入到d2.3中
lm.exam<-lm(y~x1+x2+x3+x4+x5,data=d2.3) #建立y关于x1，x2，x3，x4和x5的线性回归方程，数据为d2.3
summary(lm.exam)

运行结果如下：

从以上结果可以看出，回归方程的F值为1413，相应的P值为2.2e-16,说明回归方程是显著的，但t对应的P值却显示：常数项和变量 $x_{5}$ 是显著的，而变量 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 和 $x_{4}$ 不显著。

用逐步回归进行变量选择

为了获得“最优”回归方程，采用逐步回归方法建立 $y$ 关于 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 和 $x_{5}$ 的线性回归方程并对方程和回归系数进行显著性检验，R程序如下：

#逐步回归
lm.step<-step(lm.exam,dorection="both") #进行逐步回归

运行结果如下：

输出结果解读：

（1）采用全部自变量回归时，如果去掉变量 $x_{1}$ ，此时的AIC值最小为274.25，所以R软件去掉 $x_{1}$ 进行第二轮计算。

（2）此时AIC值为274.25，如果去掉变量 $x_{3}$ ，AIC值达到最小273.29，所以R软件去掉 $x_{3}$ 进行第三轮计算。

（3）此时AIC值为273.29，如果去掉变量 $x_{4}$ ，AIC值达到最小272.65，所以R软件去掉 $x_{4}$ 进行第四轮计算。

（4）此时AIC值为272.65，此时无论去掉哪个变量或者增加哪个变量AIC值都会增大，所以计算停止，得到最优回归模型，即 $y$ 关于 $x_{2}$ 和 $x_{5}$ 的线线性回归模型。

现在用命令summary(lm.step)来得到回归模型的如下汇总信息：

summary(lm.step) #给出回归系数的估计和显著性检验等

运行结果：

结论：注意到常数项、 $x_{2}$ 和 $x_{5}$ 都是显著的，模型也是显著的（因为P值全小于 $\alpha$ 值0.05，表示拒绝原假设），所以我们得到如下“最优”回归方程：

回归诊断

残差分析和异常点（偏离数据主体较大的点）探测

残差向量 $e=y-\hat{y}=y-X\check{\beta }$ ,是模型中随机误差项 $\varepsilon$ 的估计，残差分析可以诊断模型的基本假设是否成立（比如随机误差独立性和正态性假定），在R中，分别采用residuals(），rstandard(）和rstudent来计算普通残差、标准化残差和学生化残差。如果回归模型能够很好的描述拟合的数据，那么残差对预测值的散点图应该像一些随机散布的点，如果某个残差“很大”，则说明这个点偏离数据主体比较远，一般把标准化残差的绝对值大于等于2的观测值认为是可疑点，而把标准化残差的绝对值大于等于3的观测值认为是异常点。

下面分别用residuals(),rstandard()和rstudent()来计算上面逐步回归模型lm.step的普通残差、标准化残差和学生化残差，R程序如下：

#已经得到逐步回归模型lm.step
y.res<-residuals(lm.exam) #计算模型lm.exam的普通残差
y.rst<-rstandard(lm.step) #计算回归模型lm.step的标准化残差
print(y.rst) #输出回归模型lm.step的标准化残差
y.fit<-predict(lm.step) #计算回归模型lm.step的预测值
plot(y.res~y.fit) #绘制以普通残差为纵坐标，预测值为横坐标的散点图
plot(y.rst~y.fit) #绘制以标准化残差为纵坐标，预测值为横坐标的散点图

运行后得到回归模型lm.step的标准化残差y.rst如下：

从标准化残差可以看出，第12号点的标准化残差绝对值（3.18）大于3，因此我们认为第12号的观测值可能是异常点。

回归模型lm.step的残差散点图如图2和图3所示，可以看出，残差的分布有随着预测值先减小后增大的趋势，所以同方差性的基本假定可能不成立。

图2 普通残差图

图3 标准化残差图

如果同方差性的假定不成立，有时可以通过对因变量作适当变换来解决方差非齐问题，常见的方差稳定变换有：

（1）对数变换： $z=lny.$

（2）开方变换： $z=\sqrt{y}$

（3）倒数变换： $z=\frac{1}{y}$

下面我们用对数变换来解决解决逐步回归模型lm.step的方差非齐问题，R程序如下：

#已经得到逐步回归模型lm.step,下面对模型进行对数变换来解决方差非齐问题
lm.step_new<-update(lm.step,log(.)~.) #对模型进行对数变换
y.rst<-rstandard(lm.step_new) #计算lm.step_new的标准化残差
y.fit<-predict(lm.step_new) #计算lm.step_new的预测值
plot(y.rst~y.fit) #绘制以标准化残差为纵坐标，预测值为横坐标的散点图

图4 对数变化后的标准化残差图

比较标准化残差图图3和图4可以看出，对模型进行对数变换后的残差散点图有所改善，但是12号点是异常点，这里做一个简单的处理，去掉12号观测值，重复上述回归分析和残差分析过程， R程序如下：

#去掉12号观测值，重复上述回归分析和残差分析过程
lm.exam<-lm(log(y)~x1+x2+x3+x4+x5,data=d2.3[-c(12),]) #去掉12号观测值再建立全变量回归方程
lm.step<-step(lm.exam,direction = "both") #用一切子集回归法进行逐步回归
y.rst<-rstandard(lm.step) #计算lm.step的标准化残差
y.fit<-predict(lm.step) #计算lm.step的预测值
plot(y.rst~y.fit) #绘制以标准化残差为纵坐标，预测值为横坐标的散点图

图5 对数变换后的标准化残差：去掉了第12号观测值

回归诊断:一般的方法

上面的残差分析通过计算各个样本点对应的残差来判断模型的基本假定是否成立，以及模型中哪些点可能是异常点，但无法分析模型中的影响点，即探测哪些点对模型的推断有重要影响。下面给出回归诊断的一般方法，可以诊断模型的基本假定是否成立，哪些点是异常点，哪些点是强影响点。在R中，函数plot()和influence.measures()可以用来绘制诊断图和计算诊断统计量，下面介绍这两个函数输出的诊断结果，对上面的逐步回归模型lm.step_new进行回归诊断分析，R程序如下：

#已经获得模型lm.step_new
par(mfrow=c(2,2)) #在一个2x2网格中建立4个绘图区
plot(lm.step_new) #绘制模型诊断图
influence.measures(lm.step_new)

运行以上程序可得回归诊断图图6和如下20个观测值的诊断统计量的值：

图6 回归诊断图

图6给出了逐步回归模型lm.step_new的四个回归诊断图：

（1）残差-拟合图（Residuals vs Fitted）;(2）正态Q-Q图（Normal Q-Q）；

（3）大小-位置图（scale-Location）;（4）残差-杠杠图（Residuals vs Leverage）.

从这四个图可以看出，残差-拟合图中的点基本上呈现随机分布的模式；正态Q-Q图中的点基本落在直线上，表明残差基本服从正态分布；大小-位置图和残差杠杆图中第20号偏离中心位置最远，这说明第20号观测值可能是异常点或强影响点。

influence.measure(lm.step_new)给出了诊断统计量DFBETAS、DFFITS(dffit)、协方差比（cor.r）、库克距离（cook.d）和帽子阵（hat inf）的值：

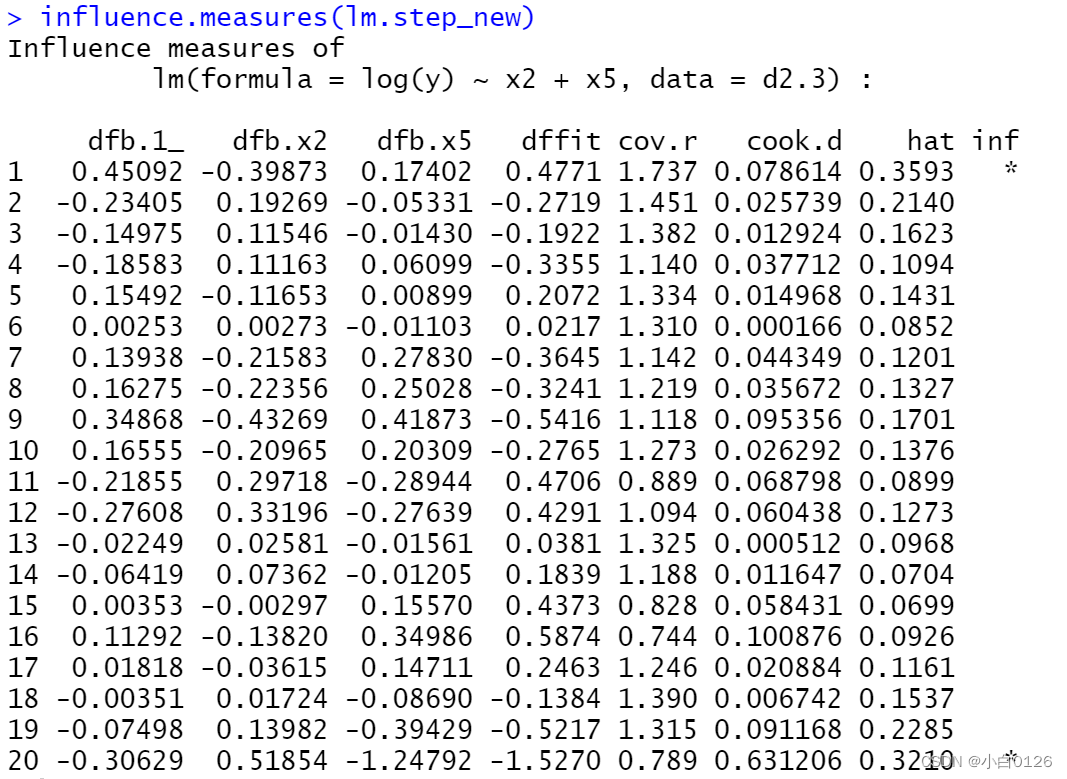
注意到第1，20号观测值右端有一个小星号标示，说明这两个点被诊断为强影响点。

需要注意的是，采用这种方法可以识别有影响的观测值，即强影响点，但是对于强影响点不能只是简单的删除它们，如何处理需要进一步讨论。

回归预测

回归预测分为点预测和区间预测两种，可以用predict()来实现，给定解释变量 $x_{2}=10903.82$

$x_{5}=7025$ ,利用回归模型lm.step进行点预测和区间预测(置信度为95%) 。R程序如下：

#假定已经获得模型lm.step
preds<-data.frame(x2=10903.82,x5=7025) #给定解释变量x2和x5的值
predict(lm.step,newdata = preds,interval = "prediction",level = 0.95) #进行点预测和区间预测

运行以上结果可得 $y$ 的点预测和区间预测结果如下：

程序中选项interval="prediction"表示要给出区间预测，选项level=0.95表示置信水平是95%。计算结果 $y$ 的点预测是11406.428，区间预测为[-571.5959,3384.451].

附录

全部R程序：

d2.3<-read.csv("ex2.3.csv",header = T) #将ex2.3.csv数据读入到d2.3中
lm.exam<-lm(y~x1+x2+x3+x4+x5,data=d2.3) #建立y关于x1，x2，x3，x4和x5的线性回归方程，数据为d2.3
summary(lm.exam)

#逐步回归
lm.step<-step(lm.exam,dorection="both") #进行逐步回归

summary(lm.step) #给出回归系数的估计和显著性检验等


#已经得到逐步回归模型lm.step
y.res<-residuals(lm.exam) #计算模型lm.exam的普通残差
y.rst<-rstandard(lm.step) #计算回归模型lm.step的标准化残差
print(y.rst) #输出回归模型lm.step的标准化残差
y.fit<-predict(lm.step) #计算回归模型lm.step的预测值
plot(y.res~y.fit) #绘制以普通残差为纵坐标，预测值为横坐标的散点图
plot(y.rst~y.fit) #绘制以标准化残差为纵坐标，预测值为横坐标的散点图


#已经得到逐步回归模型lm.step,下面对模型进行对数变换来解决方差非齐问题
lm.step_new<-update(lm.step,log(.)~.) #对模型进行对数变换
y.rst<-rstandard(lm.step_new) #计算lm.step_new的标准化残差
y.fit<-predict(lm.step_new) #计算lm.step_new的预测值
plot(y.rst~y.fit) #绘制以标准化残差为纵坐标，预测值为横坐标的散点图


#去掉12号观测值，重复上述回归分析和残差分析过程
lm.exam<-lm(log(y)~x1+x2+x3+x4+x5,data=d2.3[-c(12),]) #去掉12号观测值再建立全变量回归方程
lm.step<-step(lm.exam,direction = "both") #用一切子集回归法进行逐步回归
y.rst<-rstandard(lm.step) #计算lm.step的标准化残差
y.fit<-predict(lm.step) #计算lm.step的预测值
plot(y.rst~y.fit) #绘制以标准化残差为纵坐标，预测值为横坐标的散点图

#已经获得模型lm.step_new
par(mfrow=c(2,2)) #在一个2x2网格中建立4个绘图区
plot(lm.step_new) #绘制模型诊断图
influence.measures(lm.step_new)


#假定已经获得模型lm.step
preds<-data.frame(x2=10903.82,x5=7025) #给定解释变量x2和x5的值
predict(lm.step,newdata = preds,interval = "prediction",level = 0.95) #进行点预测和区间预测

题目数据：

t	y	x1	x2	x3	x4	x5
1999	6094	1394413	7279.56	843.23	923.24	71900
2000	6722	1478573	8344.39	1016.04	1047.26	74400
2001	7524	1534122	8901.3	1122.64	1213.44	78400
2002	8594	1608150	9790.8	1343.95	1660.23	87800
2003	8759	1587497	9166.21	1140.29	2022.19	87000
2004	12123	1767453	10903.82	1693.25	2885	110200
2005	13827	1847018	12029.23	2025.51	3102.63	121200
2006	15968	2024158	12494.21	2221.03	3452.36	139400
2007	18576.21	2227761	13187.33	2610.97	4095.4	161000
2008	19251.16	2867892.14	13002.74	2432.53	4584.44	171200
2009	23051.64	2976897.83	12647.59	2193.75	4765.62	190200
2010	26769.14	3269508.17	13376.22	2612.69	5738.65	210300
2011	29316.66	3526318.73	13542.35	2711.2	7025	264100
2012	31936.05	3804034.9	13240.53	2719.16	8318.17	295700
2013	35396.63	2122991.55	12907.78	2629.03	9818.52	326200
2014	39194.88	2032218	12849.83	2636.08	11659.32	361100
2015	43618	1943271	13382.04	2598.54	12786	400000
2016	48796.05	1900194.34	13844.38	2815.12	13513	444000
2017	55156.11	1848620.12	13948	2917	14272.74	500000
2018	61173.77	1793820.32	14119.83	3054.29	16199	553900

民航客运量变化趋势的多元线性回归模型--基于R（附R程序及讲解）