基于 librosa 的 LFCC 和 CQCC 特征提取

本文实现了基于 librosa 的 LFCC 和 CQCC 特征提取，主要参考 librosa 中 MFCC 特征提取的过程，同时使用 torchaudio 来验证 LFCC 的正确性，使用 matlab 来验证 CQCC 的正确性。

LFCC

原理

LFCC 和 MFCC 的区别就是 fliter bank 的不同，MFCC 用的是 mel freq 的滤波器组，而 LFCC 用的是频率为线性分布的滤波器组，因此只要改变 MFCC 中滤波器组的获得方式保持其他代码不变即可。

实现

基于 librosa 库实现的 LFCC 如下：

import warnings
import numpy as np
import librosa
import scipy


def linear(sr, n_fft, n_filters=128, fmin=0.0, fmax=None, dtype=np.float32):

    if fmax is None:
        fmax = float(sr) / 2
    # Initialize the weights
    n_filters = int(n_filters)
    weights = np.zeros((n_filters, int(1 + n_fft // 2)), dtype=dtype)

    # Center freqs of each FFT bin
    fftfreqs = librosa.fft_frequencies(sr=sr, n_fft=n_fft)

    # 'Center freqs' of liner bands - uniformly spaced between limits
    # * Need to validate
    linear_f = np.linspace(fmin, fmax, n_filters + 2)

    fdiff = np.diff(linear_f)
    ramps = np.subtract.outer(linear_f, fftfreqs)

    for i in range(n_filters):
        # lower and upper slopes for all bins
        lower = -ramps[i] / fdiff[i]
        upper = ramps[i + 2] / fdiff[i + 1]

        # .. then intersect them with each other and zero
        weights[i] = np.maximum(0, np.minimum(lower, upper))

    # Only check weights if f_mel[0] is positive
    if not np.all((linear_f[:-2] == 0) | (weights.max(axis=1) > 0)):
        # This means we have an empty channel somewhere
        warnings.warn(
            "Empty filters detected in linear frequency basis. "
            "Some channels will produce empty responses. "
            "Try increasing your sampling rate (and fmax) or "
            "reducing n_filters.",
            stacklevel=2,
        )

    return weights


def linear_spec(
    y=None,
        sr=22050,
        S=None,
        n_fft=2048,
        hop_length=512,
        win_length=None,
        window='hann',
        center=True,
        pad_mode='constant',
        power=2.0,
        **kwargs
):
    if S is not None:
        # Infer n_fft from spectrogram shape, but only if it mismatches
        if n_fft // 2 + 1 != S.shape[-2]:
            n_fft = 2 * (S.shape[-2] - 1)
    else:
        S = (
            np.abs(
                librosa.stft(
                    y,
                    n_fft=n_fft,
                    hop_length=hop_length,
                    win_length=win_length,
                    center=center,
                    window=window,
                    pad_mode=pad_mode,
                )
            )
            ** power
        )
    # Build a linear filter
    linear_basis = linear(sr=sr, n_fft=n_fft, **kwargs)

    return np.einsum("...ft,mf->...mt", S, linear_basis, optimize=True)


def expand_to(x, *, ndim, axes):
    try:
        axes = tuple(axes)
    except TypeError:
        axes = tuple([axes])

    if len(axes) != x.ndim:
        raise Exception(
            "Shape mismatch between axes={} and input x.shape={}".format(
                axes, x.shape)
        )

    if ndim < x.ndim:
        raise Exception(
            "Cannot expand x.shape={} to fewer dimensions ndim={}".format(
                x.shape, ndim)
        )

    shape = [1] * ndim
    for i, axi in enumerate(axes):
        shape[axi] = x.shape[i]

    return x.reshape(shape)


def lfcc(y=None,
         sr=22050,
         S=None,
         n_lfcc=20,
         dct_type=2,
         norm='ortho',
         lifter=0,
         **kwargs):
    if S is None:
        S = librosa.power_to_db(linear_spec(y=y, sr=sr, **kwargs))

    M = scipy.fftpack.dct(S, axis=-2, type=dct_type,
                          norm=norm)[..., :n_lfcc, :]

    if lifter > 0:
        # shape lifter for broadcasting
        LI = np.sin(np.pi * np.arange(1, 1 + n_lfcc, dtype=M.dtype) / lifter)
        LI = expand_to(LI, ndim=S.ndim, axes=-2)

        M *= 1 + (lifter / 2) * LI
        return M
    elif lifter == 0:
        return M
    else:
        raise Exception(
            "LFCC lifter={} must be a non-negative number".format(lifter)
        )

用 torchaudio 现有的函数进行验证：

import torchaudio
import librosa
from torchaudio.transforms import LFCC
path = ''

# torchaudio
waveform, sample_rate = torchaudio.load(full_path)
print(waveform.shape)
lfcc_transform = LFCC(
    sample_rate=sample_rate,
    n_lfcc=13,
    n_filter=128,
    speckwargs={
    
    "n_fft": 512, "hop_length": 160, },
)
torch_lfcc = lfcc_transform(waveform)
print(torch_lfcc[0, :, 0])
# librosa
wave, sr = librosa.load(full_path, sr=16000)
print(wave.shape)
librosa_lfcc = lfcc(
    y=wave, sr=sr, n_lfcc=13, n_fft=512, hop_length=240, n_filters=128, pad_mode='reflect')
print(librosa_lfcc[:, 0])

运行结果为：

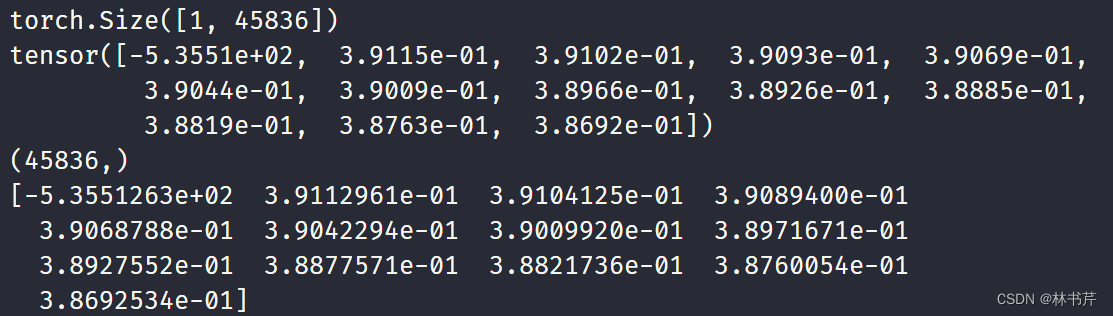
两者得到的结果基本一致。

CQCC

原理

STFT 和 CQT 可以看成是时间信号频域分析的两个同级的方法。

在 STFT 中，从长的序列中提取固定长度的片段与窗函数相乘后进行 FFT，然后重复应用滑动窗口得到最终的谱图。

STFT 实际上是一个滤波器组，定义 Q 因子为滤波器的中心频率和滤波器带宽之比：$$Q=\frac{f_k}{\delta f}$$在STFT 中，每个滤波器的带宽是恒定的，当频率从低频到高频时，Q 因子增加。

但是人类的感知系统的 Q 因子在 500Hz-20KHz 之间近似常数，因此，至少从感知角度来看，STFT对于语音信号的时频分析可能并不理想。

于是提出 CQT 变换，第一种算法由Youngberg和Boll于1978年提出的（Youngberg-Boll），而另一种算法则是由 Kashima 和MontReynaud-Kashima在1986年提出（Mont Reynaud）。在这些方法中，倍频程（octaves）是几何分布的，如下图：

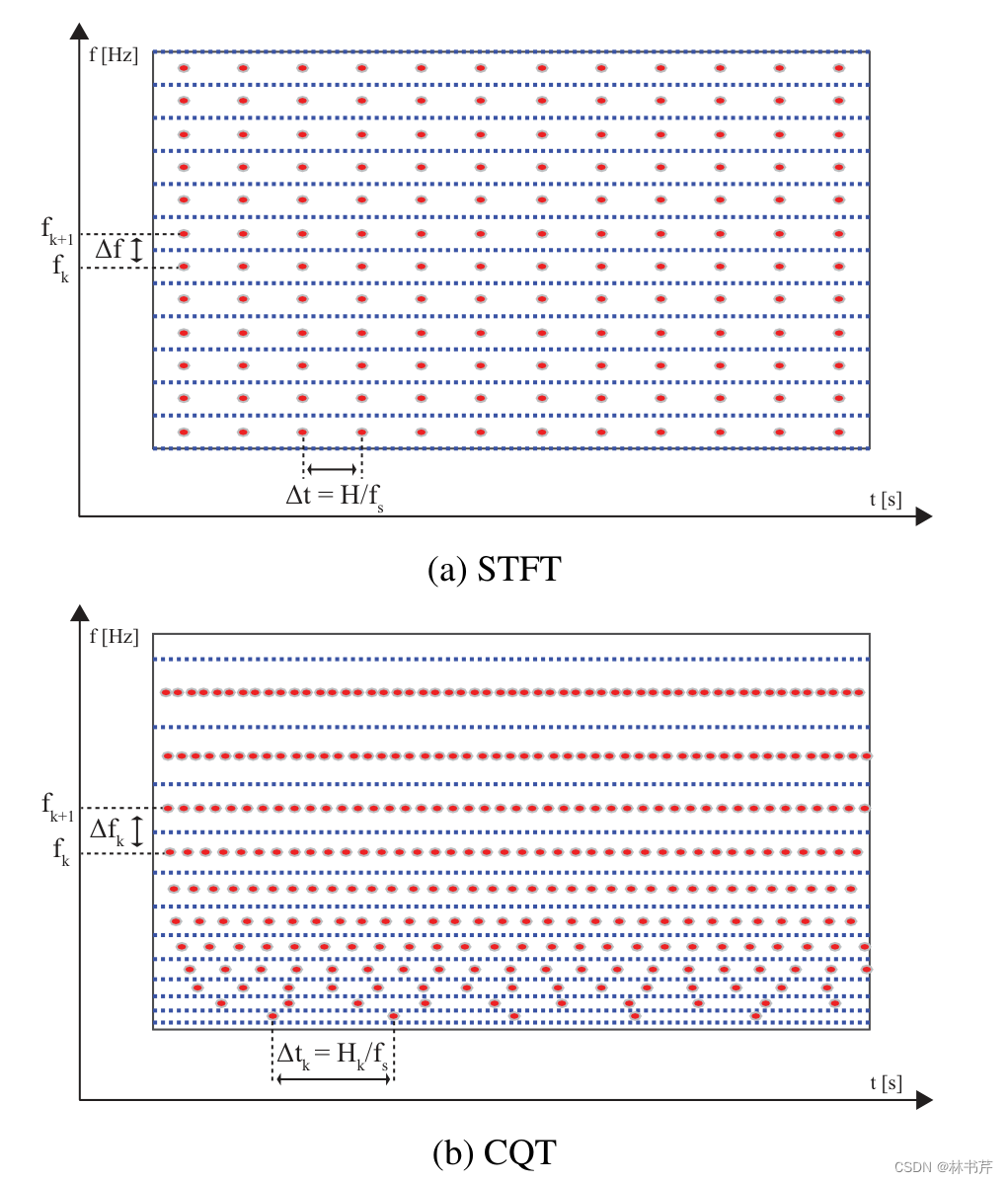
CQT 计算

离散时域信号 $x(n)$ 的 CQT 计算如下：
$$X^{CQ}(k,n)=\sum _{j=n-\lfloor N_k/2\rfloor }^{n+\lfloor N_k/2\rfloor }x(j)a_k^{\ast }\left(j-n+N_k/2\right)$$
其中，$k=1,2,\cdots ,K$ 为频率索引，$a_k^{\ast }(n)$ 为 $a_k(n)$ 的复共轭，$N_k$ 为可变的窗口大小，$\lfloor \cdot \rfloor$ 代表向下取整，基函数 $a_k(n)$ 定义如下：
$$a_k(n)=\frac{1}{C}\left(\frac{n}{N_k}\right)\exp \left[i\left(2\pi n\frac{f_k}{f_s}+{\Phi }_k\right)\right]$$
其中，$f_k$ 是第 $k$ 个频带的中心频率，$f_s$ 为采样率，$w(t)$ 为窗函数，${\Phi }_k$ 为相位偏置，缩放因子 $C$ 由下式给出：
$$C=\sum _{l=-\lfloor N_k/2\rfloor }^{\lfloor N_k/2\rfloor }w\left(\frac{l+N_k/2}{N_k}\right)$$
为了满足恒Q变换，中心频率必须满足：
$$f_k=f_1{2}^{\frac{k-1}{B}}$$
其中，$f_1$ 是最低频率带的中心频率，$B$ 确定每个倍频程的频带数。

例如，假设 $B=1$，则 $f_k=f_1{2}^{k-1}$ ，取 $f_s=8000Hz,f_1=500Hz$，则 $f_2=1000Hz,f_3=2000Hz,f_4=4000Hz,f_5=8000Hz$，不能再大了。而在DFT中，这几个频率呈线性变化。

则 Q 因子计算如下：
$$Q=\frac{f_k}{f_{k+1}-f_k}={\left(2^{1/B}-1\right)}^{-1}$$
同时窗函数长度 $N_k$ 满足：
$$N_k=\frac{f_s}{f_k}Q$$

CQCC 提取

首先 MFCC 计算如下：
$$\mathrm{MFCC}(q)=\sum _{m=1}^M\log [MF(m)]\cos \left[\frac{q\left(m-\frac{1}{2}\right)\pi }{M}\right]$$
其中，Mel 谱计算如下：
$$MF(m)=\sum _{k=1}^K{\left|X^{DFT}(k)\right|}^2{H}_m(k)$$
其中，$k$ 是DFT之后的频率索引系数，$H_m(k)$ 是第 $m$ 个Mel 尺度下的三角加权函数带通滤波器。这里，$M$ 代表滤波器的个数（$MF(m)$ 为 $M$ 点的序列），$q$ 代表离散余弦变换的点数。

倒谱分析不能直接被用于 CQT，因为 $X^{CQ}(k)$ 和 DCT 的余弦函数的尺度不同（一个是几何一个是线性）。可以通过将几何空间转换为线性空间来解决这个问题。

由于在 $X^{CQ}(k)$ 中，$k$ 个频带几何分布，信号重构的过程可以看成是前 $k$ 个频带（低频部分）进行下采样，后 $K-k$ 个频带（高频部分）进行上采样得到的，将第 $k$ 个频带的中心频率 $f_k$ 和 第一个频带的中心频率 $f_1=f_{min}$ 的频率差记为：
$$\Delta f^{k\leftrightarrow 1}=f_k-f_1=f_1\left(2^{\frac{k-1}{B}}-1\right)$$
其中，$k=1,2,\cdots ,K$ 为频率索引，距离 $\Delta f^{k\leftrightarrow 1}$ 为 $k$ 的递增函数。我们以周期 $T_l$ 进行重采样，这等效于确定一个关于 $k_l$ 的函数使得：
$$T_l=\Delta f^{k_l\leftrightarrow 1}$$
以下关注第一个倍频程，通过将第一个倍频程以周期 $T_l$ 进行 $d$ 等分，解得 $k_l$ 为：
$$\frac{f_1}{d}=f_1\left(2^{\frac{k_l-1}{B}}-1\right)\to k_l=B{\log }_2\left(1+\frac{1}{d}\right)$$
新的频率计算为：
$$F_l=\frac{1}{T_l}={\left[f_1\left(2^{\frac{k_l-1}{B}}-1\right)\right]}^{-1}$$
因此，在第一个倍频程中有 $d$ 个均匀采样，第二个倍频程中有 $2d$ 个，第 $j-1$ 个倍频程中有 $2^{j}d$ 个。

信号重构方法采用了多相抗混叠滤波器和样条插值方法，以均匀的采样率 $F_l$ 对信号进行重新采样。

最后，CQCC 系数计算如下：
$$CQCC(p)=\sum _{l=1}^L\log {\left|X^{CQ}(l)\right|}^2\cos \left[\frac{p\left(l-\frac{1}{2}\right)\pi }{L}\right]$$
其中，$p=0,1,\cdots ,L-1$ 是重采样之后得频带索引。

我理解是，比如说设置 $d=5$ ，频率 $500-1000Hz$ 之间采样就可以分成五个 $500,600,700,800,900$，而频率 $1000-2000Hz$ 之间采样分成 $2d=10$ 个频带，即 $1000,1100,1200,\cdots ,1900$，同理频率范围在 $2000-4000Hz$ 之间的频率可以分成 $2^2\ast 5=20$ 个频带，以此类推。这样虽然两两中心频率之间是几何间隔，但是采样的数量也是呈几何增长，所以最终重采样得到的频率还是线性的，从而可以进行 DCT 变换。