1. 基本动态规划：一维

明确dp[i]应该表示什么(二维情况dp[i][j])
根据dp[i]和dp[i-1]的关系寻找状态转移方程
确定初始条件，如dp[0]
定义dp数组，dp数组中的每一个元素都对应一个子问题

参考链接：图解动态规划的解题四步骤（C++/Java/Python） - 打家劫舍

70.爬楼梯

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

输入输出

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

题解

动态规划主要是找到 状态转移方程

定义一个数组dp[i]，表示走到第i阶的方法数，因为每次可以走1个或2个台阶，所以第i阶可以从i-1走一步以及从i-2走两步，所以状态转移方程 dp[i] = dp[i-1] + dp[1-2]，其中dp[1] = 1, dp[2] = 2

第一种，用一个数组存储每一种台阶数所需的方法

class Solution {
public:
    int climbStairs(int n) {
        //注意边界条件，类似于斐波那契数列
        //初始值dp[1] = 1, dp[2] = 2
        if (n <= 2)
            return n;
        vector<int> dp(n + 1, 1);
        for (int i = 2; i <= n; ++i) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};

第二种，进行空间压缩。因为dp[i]只跟dp[i-1]和dp[i-2]有关，所以用两个变量来存储即可

class Solution {
public:
    int climbStairs(int n) {
        //注意边界条件，类似于斐波那契数列
        //初始值dp[1] = 1, dp[2] = 2
        if (n <= 2)
            return n;
        int pre1 = 1; //i-2,初始值对应dp[1]
        int pre2 = 2; //i-1,初始值对应dp[2]
        int res = 0;
        for (int i = 2; i < n; ++i) {
            res = pre1 + pre2;
            pre1 = pre2;
            pre2 = res;
        }
        return res;
    }
};

198. 打家劫舍

题目描述

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。

输入输出

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

题解

寻找状态转移方程，定义一个数组dp， dp[i]，表示抢劫到第i个房子时，可以抢劫的最大数量。对于dp[i]

不抢劫这个房子，则累计的金额为dp[i-1]
若抢劫这个房子，那么累计的金额为dp[i-2]，再加上当前的房子

所以，状态转移方程为dp[i] = max(dp[i - 1]， nums[i] + dp[i-2])

定义一个dp数组

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.empty())
            return 0;
        if (nums.size() == 1)
            return nums[0];
        vector<int> dp(nums.size() + 1, 0);
        dp[1] = nums[0];//第一个房子可以抢到的钱是nums[0]
        for (int i = 2; i <= nums.size(); ++i) {
            //第i个房子对应的是i-1，dp的下标从1开始，nums的下标从0开始
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);
        }
        return dp[nums.size()];
    }
};

简化内存

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.empty())
            return 0;
        if (nums.size() == 1)
            return nums[0];
        int pre1 = nums[0];//第一个房子能抢到的钱
        int pre0 = 0;//第0个房子能抢到的钱
        int cur;//从第二个房子开始
        for (int i = 1; i < nums.size(); i++) {
            cur = max(pre1, pre0 + nums[i]);
            pre0 = pre1;
            pre1 = cur;
        }
        return cur;
    }
};

121. 买卖股票的最佳时机

题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

输入输出

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。。

题解

一维动态规划dp[i]

定义dp数组，dp[i]表示前i天的最大利润，同时记录前i天最低的价格
$d p [i] = ma x (d p [i - 1], d p [i] - min p r i ce)$
代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n <= 1)
            return 0;
        int minprice = prices[0];
        int pre1 = 0;
        int profit;
        //dp是从第二天开始，但是对应prices数组，下标是1
        for (int i = 2; i <= n; i++) {
            if (prices[i - 1] < minprice)
                minprice = prices[i - 1];
            profit = max(pre1, prices[i - 1] - minprice);
            pre1 = profit;
        }
        return profit;
    }
};

53. 最大子数组和

题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

输入输出

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

题解

经典动态规划问题（理解「无后效性」） - 最大子数组和

dp[i]：表示以 nums[i] 结尾的连续子数组的最大和。

也就是说nums[i]一定会被选取

那么有两种情况，如果dp[i-1]是负数，也就是说以nums[i-1]结尾的连续子数组的最大和仍为负数，那么nums[i]就不能加上dp[i-1]，此时直接重开

如果dp[i-1]不是负数，那么以nums[i]结尾的子数组的和要加上它
$\begin{cases} dp[i-1]+nums[i], &if (dp[i-1]>=0) \\ nums[i],&if (dp[i-1]<0) \end{cases}$
或者直接
$d p [i] = ma x (d p [i - 1] + n u m s [i], n u m s [i])$

同时注意返回值不是dp[n]，而是dp数组中的最大值，为了优化空间，每次循环都要保留最大值

代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int pre = 0;
        int res = nums[0];
        for (int i = 0; i < nums.size(); i++) {
            pre = max(pre + nums[i], nums[i]);
            res = max(pre, res);
        }
        return res;
    }
};

413. 等差数列划分

题目描述

如果一个数列至少有三个元素，并且任意两个相邻元素之差相同，则称该数列为等差数列。

例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的子数组个数。

子数组是数组中的一个连续序列。

输入输出

输入：nums = [1,2,3,4]
输出：3
解释：nums 中有三个子等差数组：[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。

题解

定义状态：dp[i]表示从nums[0]开始到nums[i]结尾的等差数列子数组的数量

由于最小的等差数列需要三个元素，所以状态转移方程
$d p [i] = d p [i - 1] + 1 ， i f (n u m s [i] - n u m s [i - 1] = n u m s [i - 1] - n u m s [i - 2])$
上式说明，如果nums[i]可以和i-1, i-2组成等差数列，那么以nums[i-1]结尾的所有数组都能与nums[i]组合成新的等差数列，此时一共有dp[i-1]个，同时还新增了[i-2, i-1, i]这个新数组，最终结果对dp进行求和

vector求和函数：accumulate

头文件是#include<numeric>，sum = accumulate(nums.begin(),nums.end(), 0)(开始位置，结束位置，初始值)

代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int N = nums.size();
        if (N < 3)
            return 0;
        vector<int> dp(N, 0);
        for (int i = 2; i < N; i++) {
            if ((nums[i] - nums[i - 1]) == nums[i - 1] - nums[i - 2])
                dp[i] = dp[i - 1] + 1;
        }
        return accumulate(dp.begin(), dp.end(), 0);
    }
};

55. 跳跃游戏

题目描述

给定一个非负整数数组 nums ，你最初位于数组的第一个下标。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

输入输出

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

题解

记录能跳到的最远位置，也就是动态规划

遍历数组，记录可以到达的最远的距离max，如果在下标i时最远距离max<i，则返回false

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int m = 0;
        for (int i = 0; i < nums.size(); ++i) {
            if (m < i)
                return false;
            m = max(m, nums[i] + i);
        }
        return true;
    }
};

方法二：动态规划

状态dp[i]表示从i开始可以跳到最远的地方

状态转移方程

如果dp[i-1]小于i，也就是说前一个根本到不了i，则返回false

否则 $d p [i] = ma x (d p [i - 1], i + n u m s [i])$

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        int pre = 0;
        for (int i = 0; i < n; i++) {
            if (pre < i)
                return false;
            pre = max(pre, i + nums[i]);
        }
        return true;
    }
};

2.基本动态规划：二维

64. 最小路径和

题目描述

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

输入输出

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SiRij4bH-1658197012984)(https://raw.githubusercontent.com/Jolene-hust/Jolene/main/img/202207181335179.png)]

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

题解

定义状态：二维数组dp[i][j]表示从左上角开始到[i, j]位置的最优路径的数字和

定义状态转移方程：对于点[i, j]，要么是[i-1,j]向右移动，要么是[i,j-1]向下移动，所以
$d p [i] [j] = min (d p [i - 1] [j], d p [i] [j - 1]) + n u m s [i] [j]$
一定要注意边界条件，最上方和最左边的变换移动只有一种

代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int col = grid.size();//多少行
        int row = grid[0].size();//多少列
        vector<vector<int>> dp(col, vector<int>(row, 0));
        for (int i = 0; i < col; i++) {
            for (int j = 0; j < row; j++) {
                //注意边界条件
                //起点
                if (i == 0 && j == 0)
                    dp[i][j] = grid[i][j];
                    //最上面的行，只能向右
                else if (i == 0)
                    dp[i][j] = dp[i][j - 1] + grid[i][j];
                else if (j == 0)
                    dp[i][j] = dp[i - 1][j] + grid[i][j];
                else
                    dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[col - 1][row - 1];
    }
};

进阶优化空间

状态dp[i][j]的值只与它的上方和左方有关，将其压缩到一维，对应于列方向

对于第i行，在遍历到第j列的时候，因为第 j-1 列已经更新过了，所以 dp[j-1] 代表 dp[i][j-1] 的值，也就是左边的值；而dp[j] 待更新，当前 dp[j] 中存储的值是在第i-1行的时候计算的，所以代表 dp[i-1][j]的值，也就是上面的值。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int col = grid.size();//多少行
        int row = grid[0].size();//多少列
        vector<int> dp(row, 0);
        for (int i = 0; i < col; i++) {
            for (int j = 0; j < row; j++) {
                if (i == 0 && j == 0)
                    dp[j] = grid[i][j];
                else if (i == 0)
                    dp[j] = dp[j - 1] + grid[i][j];
                else if (j == 0)
                    dp[j] = dp[j] + grid[i][j];
                else
                    dp[j] = min(dp[j - 1], dp[j]) + grid[i][j];
            }
        }
        return dp[row - 1];
    }
};

542. 01 矩阵

题目描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

输入输出

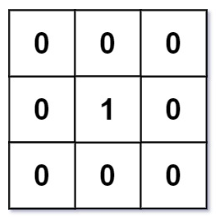
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

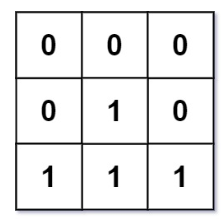
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

题解

由于涉及四个方向，所以采用两次动态规划，第一次是从左上到右下，只允许向右向下移动，第二次是右下到左上，只允许向左向上移动

定义状态：dp[i][j]表示当前点[i, j]到最近0的距离

定义状态转移方程：

对于从左上到右下的动态规划，当前点只能从左边或者上方看

如果mat[i][j]==0，那么dp[i][j]=0，否则dp[i][j]=min(dp[i][j-1], dp[i-1][j])+1

对于从右下到左上的动态规划，当前点只能从右方或者下方看

如果mat[i][j]==0，那么dp[i][j]=0，否则dp[i][j]=min(dp[i+1][j], dp[i][j+1])+1

int的最大值是INT_MAX

注意数组越界，因为dp数组的初始值是最大值

代码

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int col = mat.size();
        int row = mat[0].size();
        vector<vector<int>> dp(col, vector<int>(row, INT_MAX - 1));
        //先从左上角到右下角
        for (int i = 0; i < col; ++i) {
            for (int j = 0; j < row; ++j) {
                if (mat[i][j] == 0) {
                    dp[i][j] = 0;
                    continue;
                }
                if (i == 0 && j == 0);
                else if (i == 0)
                    dp[i][j] = min(dp[i][j], dp[i][j - 1] + 1);
                else if (j == 0)
                    dp[i][j] = min(dp[i][j], dp[i - 1][j] + 1);
                else
                    dp[i][j] = min(dp[i][j], min(dp[i][j - 1] + 1, dp[i - 1][j] + 1));
            }
        }
        //从右下角到左上角
        for (int i = col - 1; i >= 0; i--) {
            for (int j = row - 1; j >= 0; j--) {
                if (mat[i][j] == 0) {
                    dp[i][j] = 0;
                    continue;
                }
                if (i == col - 1 && j == row - 1);
                else if (i == col - 1)
                    dp[i][j] = min(dp[i][j], dp[i][j + 1] + 1);
                else if (j == row - 1)
                    dp[i][j] = min(dp[i][j], dp[i + 1][j] + 1);
                else
                    dp[i][j] = min(dp[i][j], min(dp[i][j + 1] + 1, dp[i + 1][j] + 1));
            }
        }
        return dp;
    }
};

62. 不同路径

题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径

输入输出

输入：m = 3, n = 7
输出：28

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

题解

定义状态：dp[i][j]表示从 [0, 0] 到达[i, j]一共有几条路径

定义状态转移方程：从[0, 0] 到达[i, j]，要么从[i-1, j]向下移动，要么从[i, j-1]向右移动，所以
$d p [i] [j] = d p [i - 1] [j] + d p [i] [j - 1]$
注意考虑边界条件，对于二维的一般是

if(i == 0 && j == 0)
    {}
else if(i == 0)
    {}
else if(j == 0)
	{}
else
	{}

代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 && j == 0)
                    dp[i][j] = 1;
                else if (i == 0)
                    dp[i][j] = dp[i][j - 1];
                else if (j == 0)
                    dp[i][j] = dp[i - 1][j];
                else
                    dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
            }
        }
        return dp[m - 1][n - 1];
    }
};

空间优化

定义状态：dp[j]，对于第 i 行，dp[j-1]表示第i行的第j-1列，而现在的dp[j]代表第i-1行的第j列

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> dp(n, 0);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 && j == 0)
                    dp[j] = 1;
                else if (i == 0)
                    dp[j] = dp[j - 1];
                else if (j == 0);
                else
                    dp[j] = dp[j - 1] + dp[j];
            }
        }
        return dp[n - 1];
    }
};

【LeetCode刷题笔记】动态规划合集

1. 基本动态规划：一维

70.爬楼梯

198. 打家劫舍

121. 买卖股票的最佳时机

53. 最大子数组和

413. 等差数列划分

55. 跳跃游戏

2.基本动态规划：二维

64. 最小路径和

542. 01 矩阵

62. 不同路径

猜你喜欢