【压缩感知合集1】(背景知识)香农奈奎斯特采样定理的数学推导和图解分析
【压缩感知合集2】(背景知识)信号稀疏表示的数学推导和解释理解
【压缩感知合集3】压缩感知的背景与意义
【压缩感知合集4】(背景知识)理想采样信号和随机采样信号两种采样信号的频谱分析,以及采样效果比较
主要目标
研究一下理想采样信号和随机采样信号两种采样信号的频谱,以及一些关联说明
环境假设
参数如下:
- 采样信号的时域总共点数:1024
- 针对所需要研究的两种信号(理想采样信号和随机采样信号)的采样频率:1KHz
- 两种信号的抽样频率
- 针对理想采样信号假设当这个抽样频率为10Hz时,一秒钟会有十个脉冲信号,且等间距分布,也即为这理想信号频谱的最高频上限 ω m \omega_m ωm
- 针对随机采样信号假设当这个抽样频率为10Hz时,为了方便比较一秒钟也设置相同数量的脉冲信号,间距随机,脉冲之间最小间隔可以到1
假设如下:
- 脉冲高度均为10
- 通过较窄的方波信号模拟理想采样信号中的脉冲信号
- 仅仅模拟1024点,在此1024点内理想采样信号是周期的,以此代替全时域的周期理想采样信号
图例说明如下:
每一张图图例

图一(10Hz)

图二(20Hz)

图三(50Hz)

图四(100Hz)
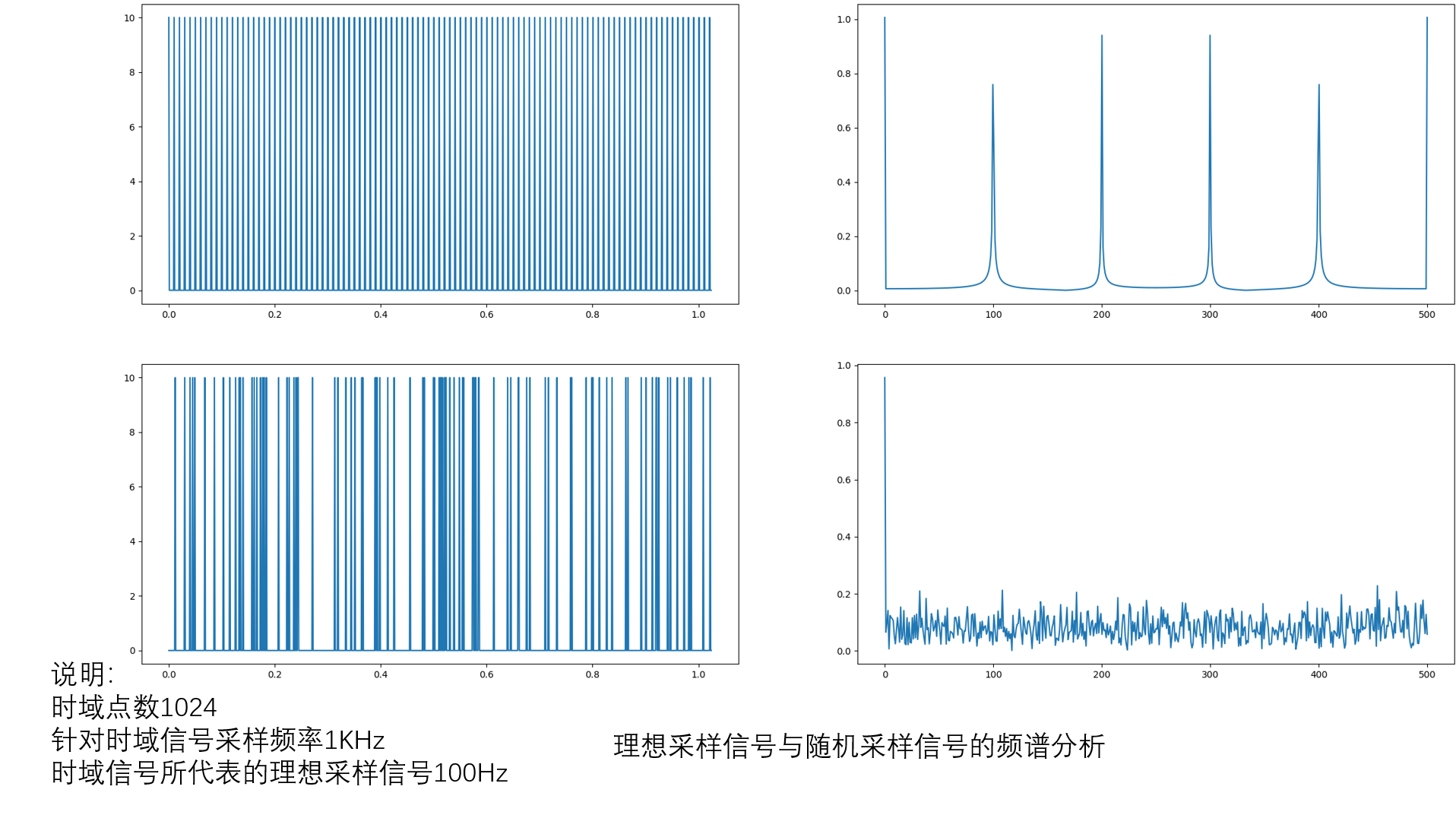
分析说明
说明1:图1->4理想采样信号频谱和数学推理结果略有不符
从10Hz到100Hz,理想采样信号的频谱(每张图的右上角)发现频谱效果变好变尖,慢慢符合奈奎斯特采样定律里面的补充证明(一个理想采样信号的频谱应该是什么样的,可以参考之前的blog 【压缩感知合集1】(背景知识)香农奈奎斯特采样定理的数学推导和图解分析)
为什么会出现这种情况呢,这次不做太多的数学推导仅仅从逻辑上尝试分析一下
原因如下:在10Hz的时候整个时域1024点就出现过10个脉冲信号,分别分布在0,100,…,1000点位上,然后做1024点的fft,但是我们要知道一个问题做完fft之后出来的1024点,和模拟域上看到的每一个频率点上都进行能量分析不一样,是存在一个理论频谱精度的,最低的精度是 Δ = 500 Hz / 512 = 0.9765625 \Delta = 500\text{Hz}/512 = 0.9765625 Δ=500Hz/512=0.9765625,也就相当于说并不能反应每一个频率的频率能量,只能精确反应 Δ \Delta Δ 整数倍上面的能量。举例 10 Hz 10\text{Hz} 10Hz最近的两个精确点位分别是 10 ∗ Δ = 9.765625 10*\Delta = 9.765625 10∗Δ=9.765625 和 11 ∗ Δ = 10.7421875 11*\Delta = 10.7421875 11∗Δ=10.7421875 。
由此我们可以做两个理论上的举例说明我们刚才的假设
举例一:当我们的频率精度足够高之后,是否可以看到更加清晰的频谱
参数设置如下
- 理想采样信号1的时域总共点数:1024
- 理想采样信号2的时域总共点数:1024*4
- 理想采样信号3的时域总共点数:1024*16
- 针对理想采样信号的采样频率:1KHz
- 3个信号的抽样频率10Hz
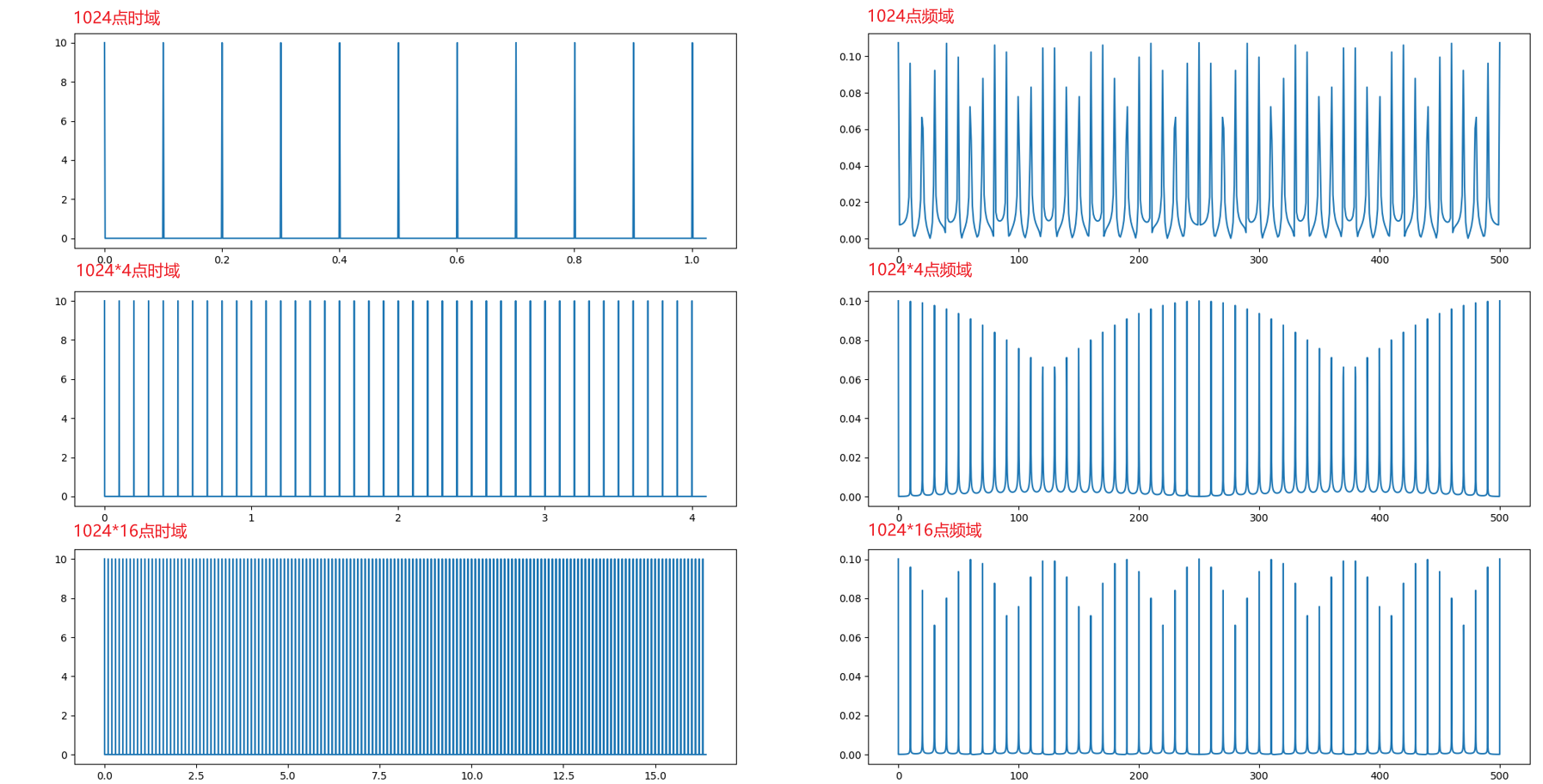
可以看到底下的泄露是很小的,随着采样点数的增加周期性愈发明显是一个一个尖锐的冲击,至于为什么高度不一样我们看第二个例子
举例二:不平频率频谱高度的问题(如果频谱能量正好在整数倍的频谱精度上面这个问题就可以被规避)
其实这个问题也是也是因为频谱精度的问题,即使例子一中第三个采样信号的点数很多,频谱精度很低还是不能正确的落在10Hz上面,这也就导致了现在所呈现出来的频谱能量周期性的涨跌,因为举例10Hz的整数倍的差值是周期性的,其实在最小公倍数处才是正确的值。但是在这个例子中我换一个方式去演绎。
参数设置如下
- 理想采样信号的时域总共点数:1024
- 针对理想采样信号的采样频率:512Hz
- 3个信号的抽样频率10Hz

在这种参数设置情况下就可以发现,每一个有频谱能量的地方都落在频率最低分辨率上。完整的根据频率周期延拓出去的脉冲形状的频谱就在这里可以被完整的展示出来。
说明2:图1->4随机采样信号与理想周期采样信号的不同是怎么来的
可以发现周期采样信号只有在自身采样频率的整数倍处会有频谱能量,其他地方都是0。
- 分析1(从数学公式推导出发):周期信号的可以写成傅里叶级数的形式(在奈奎斯特采样定理那一篇blog里面有讲过)具体形式可以写成这种形式。所以就可以很容易理解到其他的频率点上是没有能量的。
S i g n a l ( t ) = ∑ k = − ∞ ∞ a k e j k ω s t Signal(t)=\sum_{k=-\infty}^{\infty} a_{k} e^{j k \omega_{s} t} Signal(t)=k=−∞∑∞akejkωst
- 分析2(从抽象上去形容):在分析单个周期的时候,肯定是每一个频率点都会有能量的。但是在不断重复本周期的情况下,会起到一个频谱相加的作用。信号时域上的移动,频谱绝对值是不会改变的,但是相位会发生改变。周期重复其实就可以理解为一个单周期的信号经过一定的时域移动然后再相加,并且无限次重复。那这个就对应频谱中的操作就是,原始频谱经过一定的相位移动后相加。有些频率点能量会消失是因为(其实和刚才频率精度的问题类似)非与自己周期整数倍的频率点上的能量,在无数次不同相位的叠加中因为积分求和抵消了,与自己周期整数倍上的频率点上的能量会在无数次不同相位叠加中累加。
- 基于这两个分析就会发现随机采样信号,频谱是这样主要是因为,随机叠加造成的每一个小频率点都有一些频谱泄露造成。主峰高的原因主要反映在0频率点的均值能量。
说明3:随机采样信号最后可以用于压缩感知的原因
这个会在之后的blog里面再叙述一遍,这里先简单的叙述。
理想采样信号的分析
如果这些采样信号的采样点均匀分布,采样信号就会趋近于理想采样信号,理想采样信号和被采样信号进行时域卷积的时候等价于频域的相乘。会达到频谱搬移的效果,具体效果如下:

这也就是为什么需要两倍于被采样信号最高频谱进行采样的原因。
随机采样信号的分析
随着同一段时间信号内采样点的增多,随机信号频谱的主峰逐渐变高,拉高与频谱能量泄露之间的差值比重。此时随机采样信号的频谱因为主峰较高,旁瓣有不定量的随机频谱泄露,这些泄露也会小量的搬移之前稀疏的频谱,但是不会影响主峰主要的搬移效果。
具体采样过程中的效果可能是如下图所示(频谱内三个高峰都在最后一张图用不一样的颜色画出来了不一样的频谱搬移和泄漏效果,蓝色的线是三个效果的合成图)
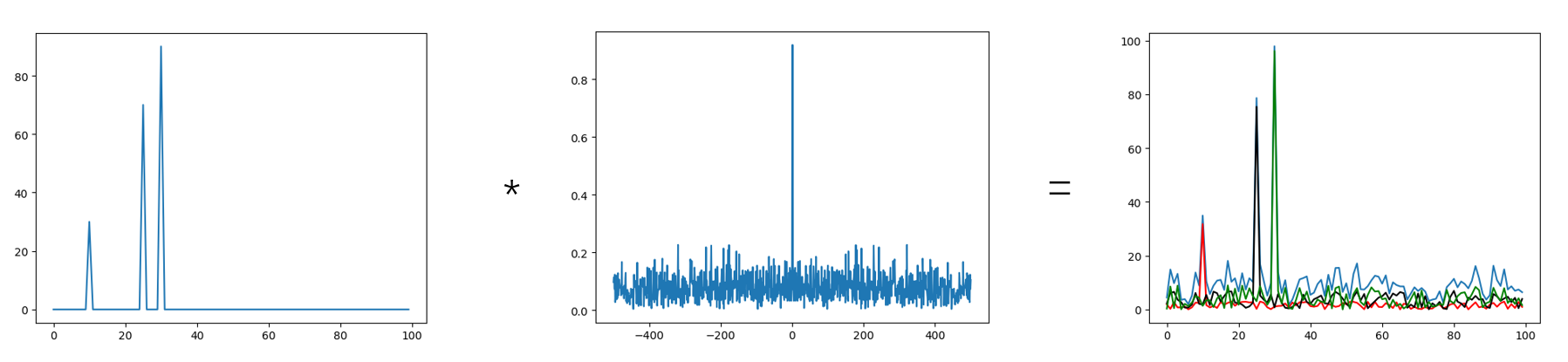
至于如何使用这个性质和怎么样对这个信号进行恢复会在下一篇里面讲一下。(如果我能讲清楚的话)