目录
1.矩阵分解(矩阵乘法)
1.1矩阵分解算法思想
首先举一个关于矩阵分解的例子。
现让五位使用者对四种商品的性价比进行打分,有如下R(5,4)的商品打分矩阵,其中打分矩阵R(m,n)是m行和n列,m表示不同的使用者,n行表示商品种类,‘-’表示使用者没有对该商品进行打分。
| 使用者\商品 | D1 | D2 | D3 | D4 |
|---|---|---|---|---|
| U1 | 5 | 3 | - | 1 |
| U2 | 4 | - | - | 1 |
| U3 | 1 | 1 | - | 5 |
| U4 | 1 | - | - | 4 |
| U5 | - | 1 | 5 | 4 |
现在要对这个表格中未打分项的值进行预测,我们可以利用矩阵分解的思想来解决,该思想可以看作是有监督的机器学习问题(回归问题)。
矩阵R可以近似的表示为P与Q的乘积:
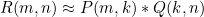
矩阵分解的过程中,将原始的R(m,n)评分矩阵分解成两个矩阵P(m,k)和Q(k,n)的乘积:
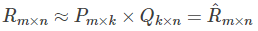
矩阵P(m,k)表示m个使用者与k个特征之间的关系矩阵,矩阵Q(k,n)可以转制为Q(n,k),Q(n,k)表示n个商品与k个特征之间的关系。在这里,k是中间变量,是自己控制的,可以使用交叉验证的方法获得最佳的K值。
1.2矩阵乘法的计算
设矩阵C、A、B满足C=A*B,则矩阵运算应该满足以下原则:
(1)C的行数应该与A的行数相同,C的列数应该与B的列数相同
(2)C的第 i 行第 j 列的元素应由A的第 i 行元素与B的第 j 列元素对应相乘,再取乘积之和。

2.梯度下降
2.1梯度下降算法思想
梯度下降法又名最速下降法。下面举例说明。
如果一个人想要下山,但是不知道怎么下山,于是决定走一步算一步,每次沿着当前最陡峭最易下山的方向前进,这样一直走下去,直到走到山脚,这里的下山最陡的方向就是梯度的负方向。梯度就是表示某一函数在该点处的方向导数沿着该方向取得较大值,即函数在当前位置的导数。
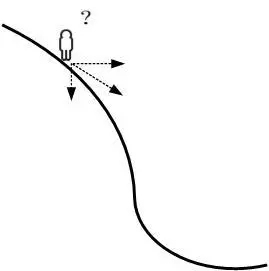

其中,θo是自变量参数,即下山位置坐标,η是学习因子,即下山每次前进的一小步(步进长度),θ是更新后的θo,即下山移动一小步之后的位置。
2.2梯度下降求解步骤

2.3梯度下降的详细推导过程

2.4梯度下降经典例题

3.矩阵分解算法推导
3.1常规推导公式

3.2正则项介绍
正则化是一种回归的形式,它将系数估计(coefficient estimate)朝零的方向进行约束、调整或缩小。也就是说,正则化可以在学习过程中降低模型复杂度和不稳定程度,从而避免过拟合的危险。通俗的说正则化就是为了防止过拟合,增强泛化能力。
正则化可分为以下三种。

3.3加正则项的推导公式
加入正则项来防止过拟合

4.矩阵分解python代码实现
import matplotlib.pyplot as plt
from math import pow
import numpy
#建立矩阵分解函数
def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):
Q=Q.T # .T操作表示矩阵的转置
result=[]#创建一个列表
for step in range(steps):
for i in range(len(R)):
for j in range(len(R[i])):
#构建损失函数
if R[i][j]>0:
eij=R[i][j]-numpy.dot(P[i,:],Q[:,j]) # .dot(P,Q) 表示矩阵内积
#根据负梯度的方向更新变量,即修改当前函数的参数值
for k in range(K):
P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
eR=numpy.dot(P,Q)
e=0
#求解所有损失函数值之和
for i in range(len(R)):
for j in range(len(R[i])):
if R[i][j]>0:
e=e+pow(R[i][j]-numpy.dot(P[i,:],Q[:,j]),2)
for k in range(K):
e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
result.append(e)#在列表尾部添加一个新的元素
#判断是否收敛
if e<0.001:
break
return P,Q.T,result
#初始矩阵
if __name__ == '__main__':
#当.py文件被直接运行时,if __name__ == '__main__'之下的代码块将被运行;
#当.py文件以模块形式被导入时,if __name__ == '__main__'之下的代码块不被运行。
R=[
[5,3,0,1],
[4,0,0,1],
[1,1,0,5],
[1,0,0,4],
[0,1,5,4]
]
R=numpy.array(R)
N=len(R)
M=len(R[0])
K=2
#定义P、Q矩阵
P=numpy.random.rand(N,K) #随机生成一个 N行 K列的矩阵
Q=numpy.random.rand(M,K) #随机生成一个 M行 K列的矩阵
nP,nQ,result=matrix_factorization(R,P,Q,K)
print("原始的评分矩阵R为:\n",R)
R_MF=numpy.dot(nP,nQ.T)
print("经过MF算法填充0处评分值后的评分矩阵R_MF为:\n",R_MF)
#-------------损失函数的收敛曲线图---------------
n=len(result)
x=range(n)
plt.plot(x,result,color='r',linewidth=3)
plt.title("Convergence curve")
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()
运行结果:

