最小二乘法
数据拟合的目的:
1.从大量实验数据(xi,yi) (i=0,1,2…m)中寻找其函数关系 y = f(x)的近似表达式y=p(x)
2.插值法要求插值曲线严格通过每个数据点,在n比较大时,差值多项式往往是告辞多项式,容易出现震荡现象。
3.当不必要求近似函数y=p(x)过所有点,即yi=p(xi) i=0,1,2 … m,只要求其误差ri=p(xi)-yi i = 0,1,2 … m,按某种标准最小,以反映原函数整体的变化趋势消除局部波动影响,这样的函数y=p(x)称为拟合函数。
最小二乘法的基本原理
求p(x)使
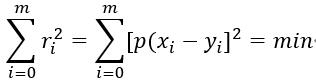
多项式拟合步骤
定义:对给定一组数据(xi,yi) (i=0,1,2 ... m),求次数不超过n的多项式

使其满足

该曲线拟合称为多项式拟合,满足上式Pn(x)叫最小二乘拟合多项式,当n = 1时,一次多项式又叫直线拟合。

由多元极值必要条件知 aj满足

即

化为矩阵形式为:

称为正规方程组或法方程组
且有如下定理:
定理1:设点xi互异,则法方程组存在且唯一。
对给定数据进行数据拟合
xi -2 -1 0 1 2
yi 0.2 0.8 2 3 4
输出拟合函数,以及平方误差
使用最小二乘法进行数据拟合,第一步先构造正规方程组,
这里采用的方法为:
将输入的数据保存在两个一位数组x,y中,声明tempx[2n]数组,保存的是Σx^i
,使用下标访问对应次方的和。其次声明tempy[n]数组,保存Σxi^nyi.
使用到的变量
double zhengGui[8][9] = {
0 };
double x[8] = {
0 }; //保存拟合数据xi
double y[8] = {
0 }; //保存拟合数据yi
double tempx[15] = {
0 }; //使用下标保存 xi^n的和
double tempy[9] = {
0 }; //保存xi^n*yi
完整代码:
#include<iostream>
#include<math.h>
using namespace std;
double zhengGui[8][9] = {
0 };
double x[8] = {
0 }; //保存拟合数据xi
double y[8] = {
0 }; //保存拟合数据yi
double tempx[15] = {
0 }; //使用下标保存 xi^n的和
double tempy[9] = {
0 }; //保存xi^n*yi
void printGuass(double a[8][9], int n) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n + 1; j++)
printf("%12f,", a[i][j]);
printf("\n");
}
}
struct Max
{
double value = 0;
int row = 0; //保存行
int col = 0; //保存列
};
void SelectMainE(int n)
{
double temp; //记录消元时的因数
Max max;
for (int m = 1; m <= n; m++) {
max.value = -1000000000;
for (int i = m; i <= n; i++)
{
if (abs(zhengGui[i][m]) > max.value) {
max.value = abs(zhengGui[i][m]);
max.row = i;
max.col = m; //记录主元素列坐标
}
}
if (max.row != m || max.col != m) {
for (int i = m; i <= n + 1; i++) {
swap(zhengGui[m][i], zhengGui[max.row][i]);
}//行变换
}
for (int j = m + 1; j <= n; j++) {
//消元
temp = zhengGui[j][m] / zhengGui[m][m];
for (int k = m; k <= n + 1; k++)
zhengGui[j][k] -= zhengGui[m][k] * temp;
}
}
}
void Gauss(int n) {
SelectMainE(n);
//回代求解
for (int i = n; i >= 1; i--) {
//回代求解
for (int j = i + 1; j <= n; j++)
zhengGui[i][n + 1] -= zhengGui[i][j] * zhengGui[j][n + 1];
zhengGui[i][n + 1] /= zhengGui[i][i];
}
}
void GaussCol(int n) {
printGuass(zhengGui, n);
cout << endl;
Gauss(n);
for (int i = 1; i <= n; i++) {
cout << "a" << i << "=" << zhengGui[i][n + 1] << endl;
}
}
void getZhengGui(int m,int n) {
//n为拟合多项式最高次数
//m为数据个数
zhengGui[1][1] = m + 1;
for (int i = 1; i <= 2 * n; i++) {
for (int j = 1; j <= m; j++) {
tempx[i] += pow(x[j], i);
}
}
for (int i = 1; i <= n + 1; i++) {
for (int j = 1; j <= m; j++) {
if (i == 1) {
tempy[i] += y[j];
}
else {
tempy[i] += y[j] * pow(x[j],i - 1);
}
}
}
for (int i = 2; i <= n + 1; i++) {
//构造正规方程组的第一列,从第2行到第n+1行
zhengGui[i][1] = tempx[i - 1];
}
int count = 1;
for (int i = 2; i <= n + 1; i++) {
//构造正规方程组的第2列到第n+1列
//外循环控制列数,内循环控制行数
for (int j = 1; j <= n + 1; j++) {
zhengGui[j][i] = tempx[count];
count++;
}
count -= n;
}
for (int i = 1; i <= n + 1; i++) {
//构造第n+2列保存xi^n*yi
zhengGui[i][n + 2] = tempy[i];
}
}
void disp(int n) {
cout << "\n拟合函数为:";
cout << "f(x)=";
printf("%.3lf",zhengGui[1][n + 1]);
for (int i = 2; i <= n; i++) {
printf("+%.3lf*",zhengGui[i][n + 1]);
cout<< "x^" << i - 1;
}
}
//计算平方误差
double niHeFunction(double x0,int n,int m) {
//n表示矩阵中保存结果的最后一列
//m为数据个数
double sum = 0;
sum += zhengGui[1][n + 1];
for (int j = 2; j <= n; j++) {
sum += pow(x0,j-1) * zhengGui[j][n + 1];
}
return sum;
}
void I(int m,int n) {
//m为数据个数
//n 拟合次数
double sum = 0;
for (int i = 1; i <= m; i++) {
sum += pow(y[i] - niHeFunction(x[i], n, m),2);
}
cout << "\n平方误差为:" << sum;
}
void reset() {
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 9; j++) {
zhengGui[i][j] = 0;
tempy[j] = 0;
}
}
for (int i = 0; i < 15; i++) {
tempx[i] = 0;
}
}
void LeastSquares() {
cout << "请输入需要拟合的数据的个数:";
int m = 0;
cin >> m;
cout << "\n请输入xi:";
for (int i = 1; i <= m; i++) {
cin >> x[i];
}
cout << "\n请输入yi:";
for (int i = 1; i <= m; i++) {
cin >> y[i];
}
int cishu = 0;
for (int i = 1; i <= m; i++) {
cishu = i;
getZhengGui(m, cishu);
cout << "\n++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++" << endl;
cout << "\n当前拟合函数的最高次数为:" << cishu << endl;
//求解正规方程组
cout << "\n正规方程组为:" << endl;
GaussCol(cishu+1);
disp(cishu + 1);
I(m,cishu+1);
cout << "\n++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++" << endl;
reset();
}
}
int main() {
LeastSquares();
return 0;
}
运行结果
程序会使用最小二乘法对给输入数据进行拟合,打印最高次数为1-6次的拟合函数并每次将正规矩阵打印出来(求解正规矩阵的方法是高斯列主消元法),并将每次拟合结果进行误差分析,打印输出平方距离。对于正确性,使用matlab对所给出的6个拟合函数进行绘图结果如下:

此时的输入数据为:
xi 0 0.5 0.6 0.7 0.8 0.9 1.0
yi 1 1.75 1.96 2.19 2.44 2.71 3.00
