一.实验目的
通过算法确定RSA算法中的公钥n
在RSA算法中,n是由两个素数的乘积来确定的。但由于n是公开的,为了避免攻击者用穷举法求出p和q(根据n=pq),应该从足够大的集合中选取p和q,即p和q必须是大素数。但目前还没有有效的方法可以产生任意大素数,用Miller-Rabin素性概率检测法能够有效地实现素数的生成。
Miller-Rabin算法可以确定一个整数是合数,但不能确定其一定是素数。不过尽管如此,该算法所产生的数几乎可以肯定是素数
二.实验原理
数学原理
算法的主要思想就是检验数是否满足特定的素数条件,这些条件在Miller-Rabin算法中是一个强概率条件, 所以通过条件检验的数,一般能以大概率认定为素数.
设检验数n>2是一个奇数,可以改写为n=2k∗q+1,其中k,q均为正数,且q为奇数.
引入一个基数a,(0<a<n),当满足以下的同余式条件之一时,称n为关于a的强概率素数
条件包括
(1)aq≡1(mod n)

(2)a2kq≡1(mod n)
(3)a2k-1q≡1(mod n) or a2-1kq≡p-1(mod n)
主要依据是
费马小定理
对于素数n,和正数a,且n不整除a,有an−1≡1(mod n)和基于1(mod n)的平方根只有1,-1
算法示例
举几个例子方便直观感受
(1)n=233
233−1=23∗29,这里的k=3,q=29,选择a=2
检验: aqmod n=229mod233=1所以判定为素数
(2)n=237
237−1=22∗59,这里的k=2,q=59,选择a=2
检验: aqmod n=259mod237=167所以判定为合数(非素数)
三.实验步骤
Miller-Rabin算法检测步骤:
1.任取一个大奇数N。
2.任取一正整数a∈{2,3,..,N-2}。
3.如果gcd(a,N)=1且a∉PN,则称N通过一次测试,即N有可能是素数;否则,N必定为合数。
4. 重复上述步骤2、3,任意选择不同的a共s次,以进行测试。
用Matlab实现如下:
n=1097;
k=1;
%%计算k和q
while true
if mod((n-1),power(2,k))==0 %%能整除出q
q = (n-1)/2^k;
if mod(q,2) ==1%%q要为奇数
break
else
k=k+1;
end
else
k=k+1;
end
if k == 9999999%%设置查找上限,避免一直找下去
flag=0;
break;
end
end
if flag==0%%当找不到k和q时直接判断是否为素数
for i=2:sqrt(n)%%遍历2~根号n
if mod(n,i)==0%%n是i的倍数,则n不是合数
n="无法求出k和q,n为合数";
else
n="无法求出k和q";%%当n不是合数但是又无法求出k和q
end
end
else
for a=2:n-1
if mod((a^q),n)==1
n="n通过了Miller-Rabin素数测试,是素数";
else
for j = 1:1:k
if mod((a^(2^((j-1)*q))),n)==n-1
n= "n通过了Miller-Rabin素数测试,是素数";
else
for i=2:sqrt(n)
if mod(n,i)==0
n="n是合数";
end
end
end
end
end
end
end
选取不同的n进行测试:
n=100、97、17、29、47、83、99
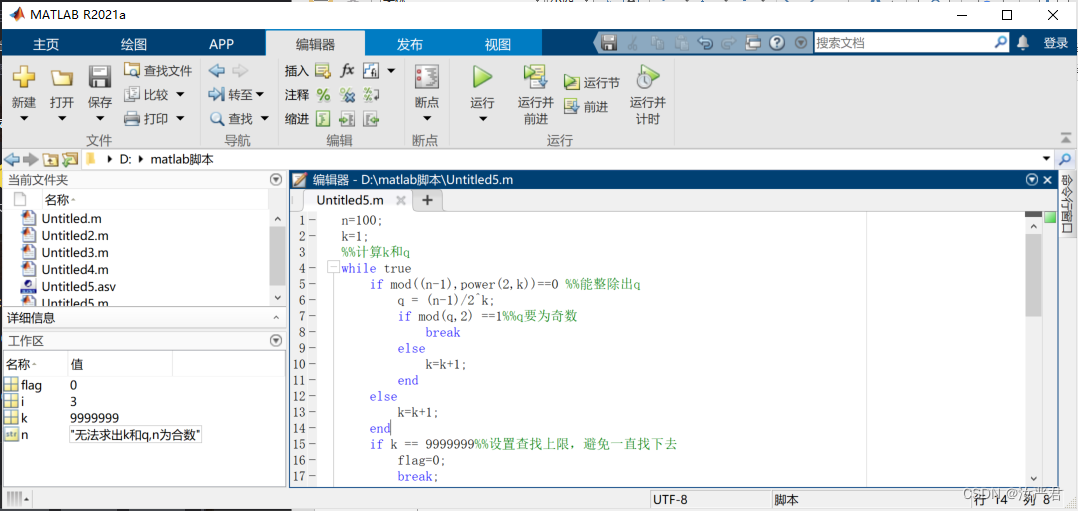
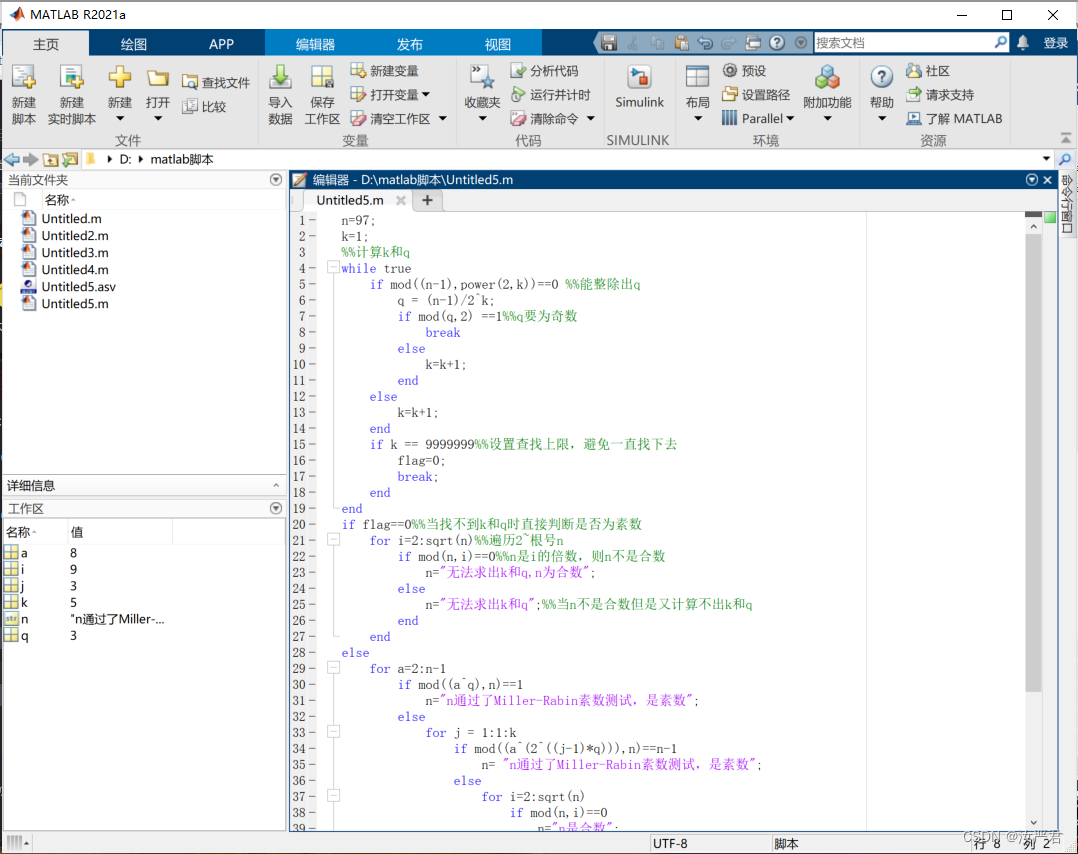
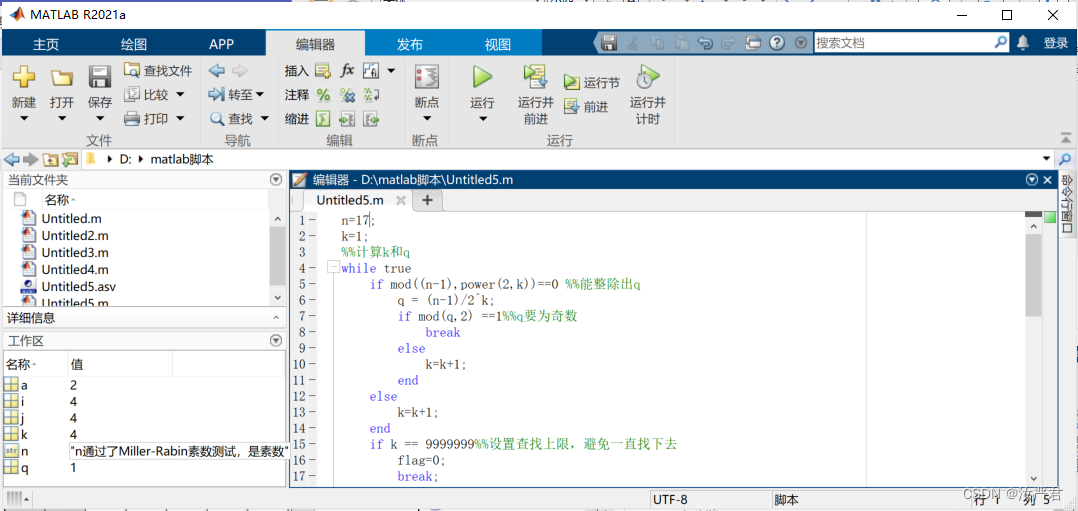

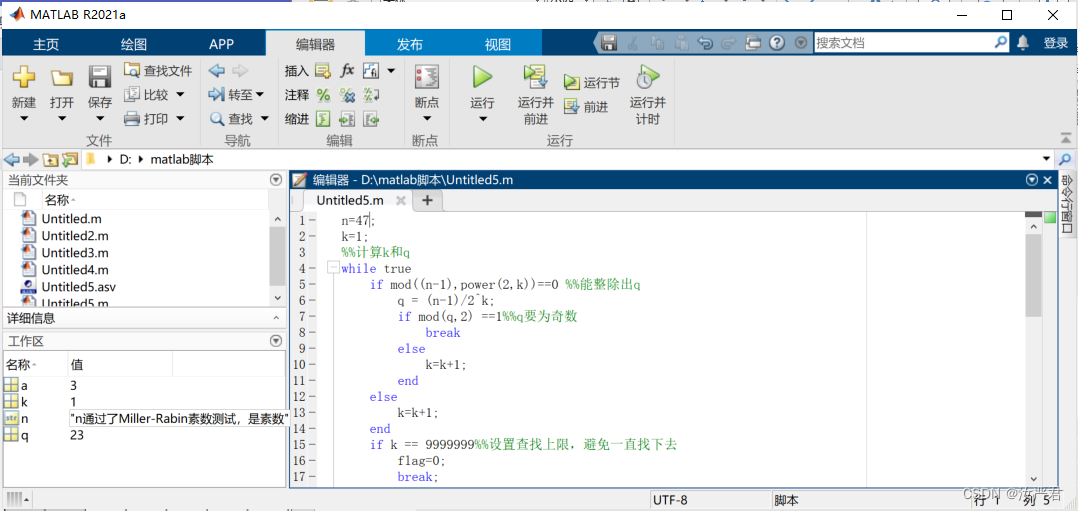
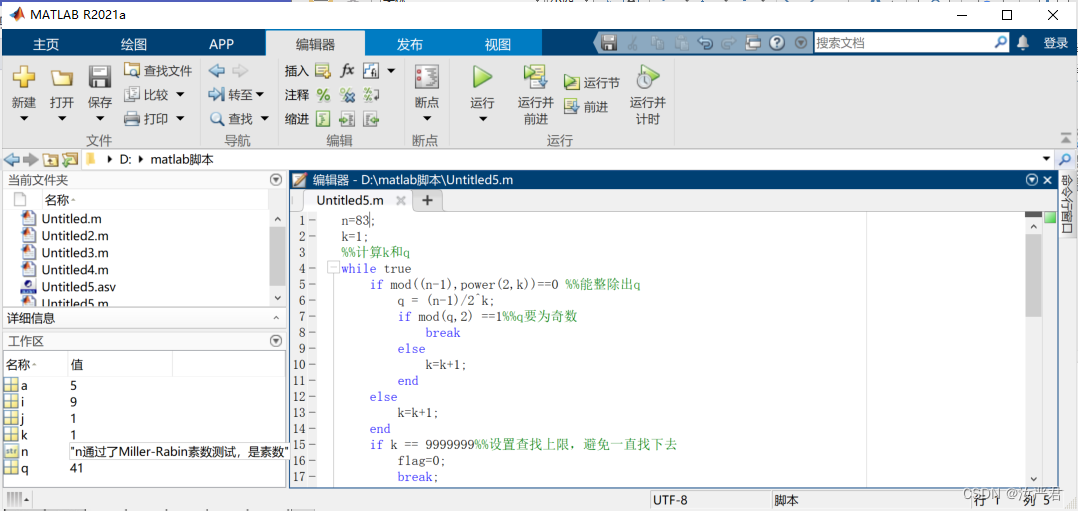
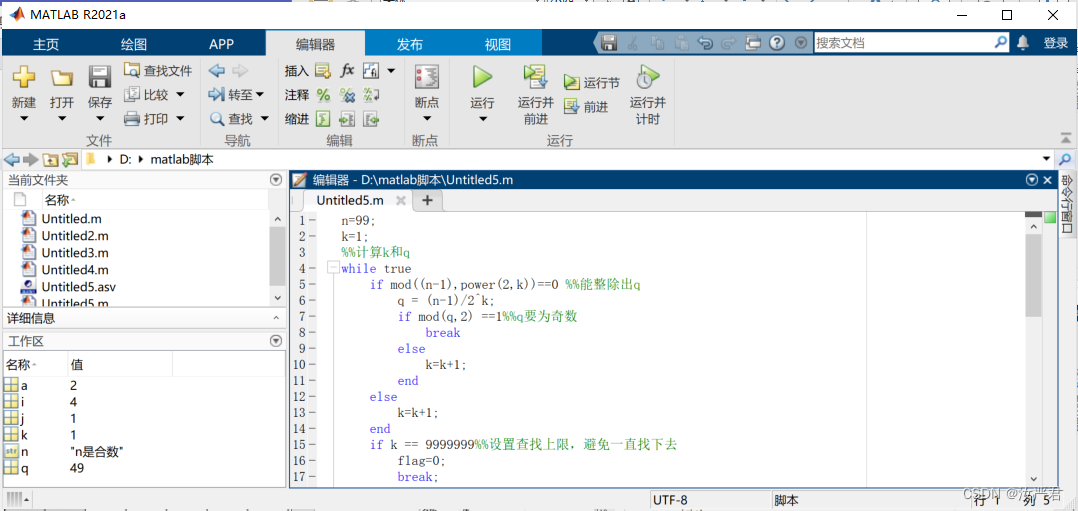
C++代码实现如下:
#include <bits/stdc++.h>
using namespace std;
//实用函数做模幂运算。
// 返回 (x^y) % p
int power(int x, unsigned int y, int p)//x为随机数a,y为q,p为n
{
int res = 1; // 初始化结果
x = x % p; //1<a<n-1,如果x大于或等于p,则更新x
while (y > 0)
{
//如果y是奇数,则用结果乘以x。
if (y & 1)
res = (res*x) % p;
y = y>>1; // 左移,相当于y = y/2
x = (x*x) % p;
}
return res;
}
//此函数用于所有s次试验。如果n是合数的,则返回false;如果n可能是素数,则返回true。q是奇数,使得对于某些r>=1,q*2^r=n-1
bool miillerTest(int q, int n)
{
//在【2,n-2之间】选择一个随机数a,同时保持n>4
int a = 2 + rand() % (n - 4);
// 计算 a^d % n
int x = power(a, q, n);
//保持x的平方下列情况之一。
// (i) q does reach n-1
// (ii) (x^2) % n is 1
// (iii) (x^2) % n is n-1
if (x == 1 || x == n-1)
return true;
while (q != n-1)
{
x = (x * x) % n;
q *= 2;
if (x == 1) return false;
if (x == n-1) return true;
}
// 返回值表示合数
return false;
}
//如果n是合数的,则返回false;如果n可能是素数,则返回true。k是确定精度水平的输入参数。k值越高表示精度越高。
bool isPrime(int n, int s)
{
if (n <= 1 || n == 4) return false;
if (n <= 3) return true;
//对于某些r>=1,求r使得n=2^r*d+1
int q = n - 1;
while (q % 2 == 0)
q /= 2;
//给定“s”次的变换
for (int i = 0; i < s; i++)
if (!miillerTest(q, n))
return false;
return true;
}
int main()
{
int s = 99;//迭代次数
cout << "所有小于100的素数: \n";
for (int n = 1; n < 100; n++)
if (isPrime(n, s))
cout << n << " ";
return 0;
}
运行效果:

与教材数据做对比
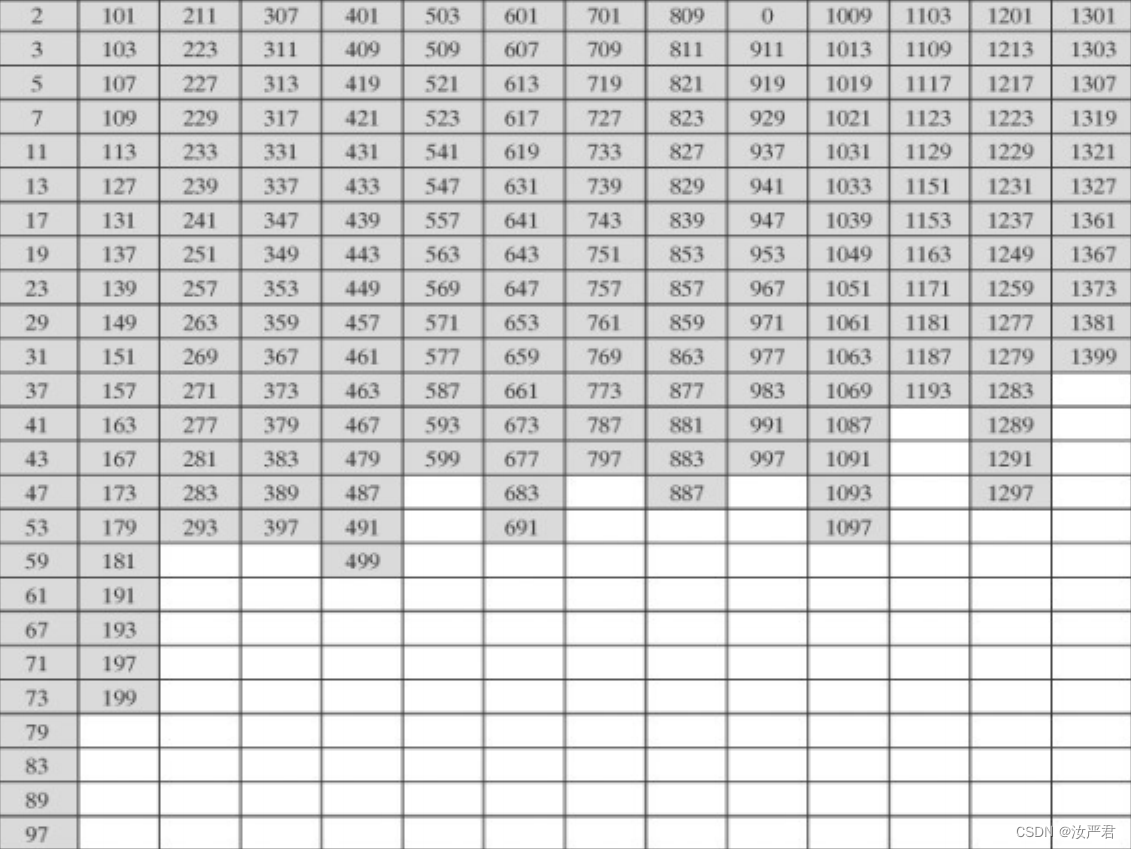
从结果上看,基本验证了算法的可行性
至此,本次实验结束,实验达到了预期效果
四.实验总结
本次实验学习了Miller—Rabin素性检测算法,Miller-Rabin素数检验或Rabin-Miller素数检验是一种概率素数检验:一种确定给定数是否可能是素数的算法,类似于费马素数检验和Solovay-Strassen素数检验。作为实践中使用比较广泛的素性检验算法的一种,Miller-Rabin算法最早在1976年由Gary L. Miller提出(当时该算法是确定性的),并在1980年由Michael O. Rabin改进为无条件的概率算法.