这篇文章的主要记录我对于基于优化方法的视觉里程计的理解,并利用C++代码实现了一个输入两张图片和图片对应的深度,输出一个位姿变换的视觉里程计算法。
视觉里程计是视觉SLAM中最重要的部分之一,其位于整个视觉SLAM的前端,核心任务是为整个SLAM过程提供一个不错的位姿估计,实现视觉里程计的方法有很多,本文主要探讨基于优化方法实现的视觉里程计的原理和代码实现。
(如果有错误或者不准确的地方,请大家批评指正!)
基于优化方法实现的视觉里程计主要流程如下:
- 从相机中读取两帧图片,并提取特征点,进行特征点匹配。
- 利用匹配好的特征点进行重投影,从而构建重投影误差,将整个问题转换为一个最小二乘问题。
- 利用优化方法求解。
我们最关注的位姿在重投影过程中用到了,所以重投影误差越小,那么用来进行重投影的位姿就越好。接下来结合代码一起看整个过程,必要的时候会补充一些理论和公式。
第一步,提取特征点和特征点匹配
Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);
assert(img_1.data && img_2.data && "Can not load images!");
vector<KeyPoint> keypoints_1, keypoints_2;
vector<DMatch> matches;
find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
//完成特征点的提取和匹配之后,图一的特征点保存在keypoints_1中
//matches中保存的是两张图匹配好的特征点特征点的提取和匹配十分简单,主要调用了opencv自带的函数,这里就不多赘述,最后得到的结果是三个容器,keypoints_1,keypoints_2,matches,保存的是特征点的像素坐标(一定要注意每个容器中放的是什么坐标,视觉slam中涉及到像素坐标,相机坐标,世界坐标,归一化平面坐标等多个坐标系的坐标转换,如果不搞清楚很容易出错)。
第二步,进行坐标变换,为后续的重投影做准备
这一步的转换用到了双目相机的成像模型,双目相机可以根据焦距、基线、视差等还原出相片上每一个像素点的深度,从而做到把2d的像素点转换成3d的世界坐标点。
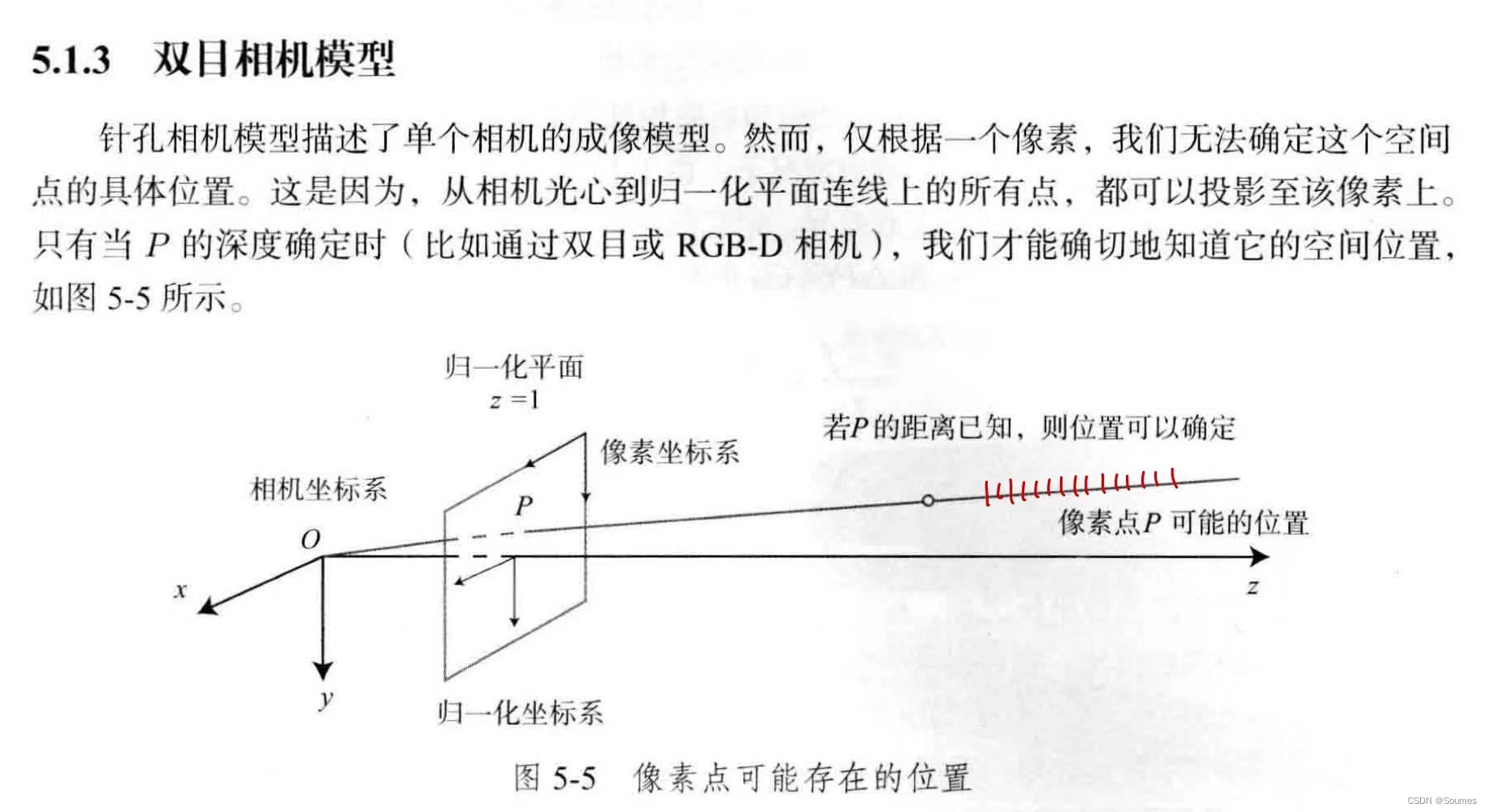
双目相机模型(摘自视觉slam14讲)
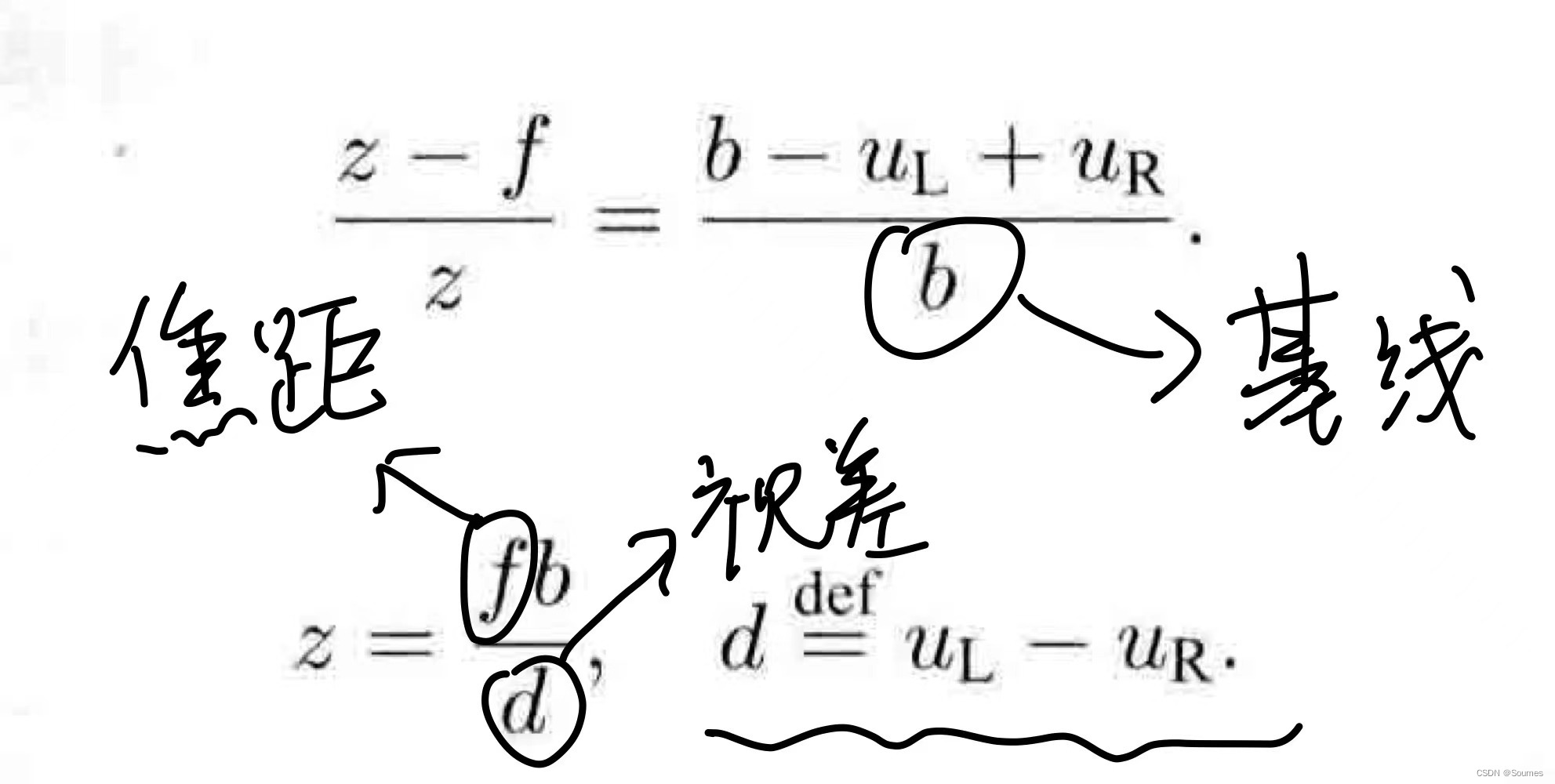
z表示深度,这是深度的计算公式
具体代码如下:
// 第二步是利用双目相机的深度图,还原匹配的特征点的世界坐标
Mat d1 = imread(argv[3], CV_LOAD_IMAGE_UNCHANGED); // 深度图为16位无符号数,单通道图像
Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);//相机内参
vector<Point3f> pts_3d;//特征点的世界坐标容器
vector<Point2f> pts_2d;//特征点的像素坐标容器
//遍历匹配好的特征点
for (DMatch m:matches) {
ushort d = d1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
//上述代码用来获取某一个点的深度
//keypoints_1[m.queryIdx].pt.y和.x作为索引来使用,所以转换为int类型,代码可以化简为ushort d = d1.ptr<unsigned short>(y')[x'];
//意思就是获取y行x列的深度值
if (d == 0) // bad depth
continue;
//这里是进行一个归一化的操作,5000是一个常用的经验值,不太明白
float dd = d / 5000.0;
//像素坐标转换到相机坐标,由于要获取世界坐标,所以先把像素坐标转换到相机坐标
Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
//通过乘以深度将相机坐标转换到了世界坐标,这里涉及到双目相机的模型知识,注意这里的世界坐标来源是图一的特征点
pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));
//图2的特征点直接插入到pts2d中去了,作为后面构建重投影误差的观测,这里是像素坐标
pts_2d.push_back(keypoints_2[m.trainIdx].pt);
//pts3d放的是由图一特征点得到的世界坐标,后面用来重投影(估计值
//pts2d得到的是由图二特征点得到的像素坐标,后面座位重投影中的观测(真值
//由于是遍历matches得到的,所以pts3d和pts2d的点都是匹配上的特征点,是对应的
}完成转换后,得到了pts3d和pts2d,这里要注意一下这两个容器中的内容,pts3d放的是由图一特征点得到的世界坐标,后面用来进行重投影,作为估计值,pts2d得到的是由图二特征点得到的像素坐标,后面作为重投影中的观测,也就是真值,由于是遍历matches得到的,所以pts3d和pts2d的点都是匹配上的特征点,是一一对应的。
第三步,构建重投影误差,建立最小二乘问题,采用高斯牛顿方法进行求解
先贴代码,然后再把代码拆开了一部分一部分讲解
void bundleAdjustmentGaussNewton(
const VecVector3d &points_3d,
const VecVector2d &points_2d,
const Mat &K,
Sophus::SE3d &pose) {
//传入进来的points3d是世界坐标下的图一特征点
//传入进来的points2d是像素坐标下的与图一特征点匹配的图二像素点
typedef Eigen::Matrix<double, 6, 1> Vector6d;
const int iterations = 10;//迭代次数
double cost = 0, lastCost = 0;//代价值
//相机内参
double fx = K.at<double>(0, 0);
double fy = K.at<double>(1, 1);
double cx = K.at<double>(0, 2);
double cy = K.at<double>(1, 2);
for (int iter = 0; iter < iterations; iter++) {
//初始化海森矩阵
Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
//初始化误差矩阵
Vector6d b = Vector6d::Zero();
cost = 0;
// compute cost
for (int i = 0; i < points_3d.size(); i++) {
//因为此时的坐标是世界坐标,因此要转到相机坐标下
Eigen::Vector3d pc = pose * points_3d[i];//这里用的是世界坐标到相机坐标的公式
//pc就是相机坐标下的三维点
double inv_z = 1.0 / pc[2];//1/Z,在相机转像素用到
double inv_z2 = inv_z * inv_z;//在雅可比计算中才用到
Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);
//再把相机坐标一步到位投影到像素坐标,经历了内参和外参
Eigen::Vector2d e = points_2d[i] - proj;//构建最小二乘方程
cost += e.squaredNorm();//但是误差不能用上面的来描述,用的是平方范数
Eigen::Matrix<double, 2, 6> J;
//下面是雅可比矩阵的计算,通过求导推倒出雅可比矩阵,然后把值都代进去算,每个值都是知道的
J << -fx * inv_z,
0,
fx * pc[0] * inv_z2,
fx * pc[0] * pc[1] * inv_z2,
-fx - fx * pc[0] * pc[0] * inv_z2,
fx * pc[1] * inv_z,
0,
-fy * inv_z,
fy * pc[1] * inv_z2,
fy + fy * pc[1] * pc[1] * inv_z2,
-fy * pc[0] * pc[1] * inv_z2,
-fy * pc[0] * inv_z;
//计算海森举证
H += J.transpose() * J;
//计算误差矩阵
b += -J.transpose() * e;
}
Vector6d dx;
//求解dx,dx就是代估计量,在这里就是位姿
dx = H.ldlt().solve(b);//求解用到了海森矩阵和误差矩阵,就是上面求的
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
// cost increase, update is not good
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// update your estimation
//通过dx来更新位姿,从而达到视觉里程计的目的,提供一个不错的位姿供后续操作
pose = Sophus::SE3d::exp(dx) * pose;
lastCost = cost;
cout << "iteration " << iter << " cost=" << std::setprecision(12) << cost << endl;
if (dx.norm() < 1e-6) {
// converge
break;
}
}
cout << "pose by g-n: \n" << pose.matrix() << endl;
}首先明确重投影误差的概念,举个简单的例子,在你的面前放了一个水壶,你在不同的位置对水壶拍了两张照片,在这个过程中水壶并没有移动,那么按理来说两张照片中的水壶在世界坐标中的位置应该是相同的,那么利用第一张照片得到水壶的世界坐标,并将水壶通过一个估计的位姿变换投影到第二张照片上去,这个过程就是重投影,由于位姿变换是估计的,不一定准确,所以投影过去的位置和水壶在第二张照片上的位置肯定有一定的差距,这两个位置之间的差距就是重投影误差,下面详细说一下这个过程。
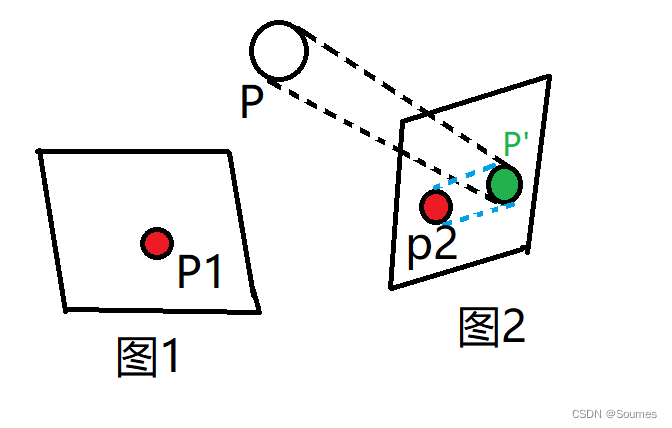
如图所示,图1和图2为对P这个物体的两次拍摄,这个过程中P没有动过,但是拍摄的位置和姿态有了变换,我们构建重投影误差来求这个位姿的变换。首先通过图1和图2的特征点匹配,我们得到了一对匹配好的特征点P1和P2,随后我们利用P1的像素坐标+相机的深度(没错我们用的是双目相机,这个过程就和上面的第二部分一样)还原P的世界坐标P(X,Y,Z),得到P的世界坐标之后,我们开始做投影。
投影的第一步是把P点从世界坐标系转换到拍摄图二时的相机坐标系下,这个过程依据下面这个公式,位姿就是在这里用到。
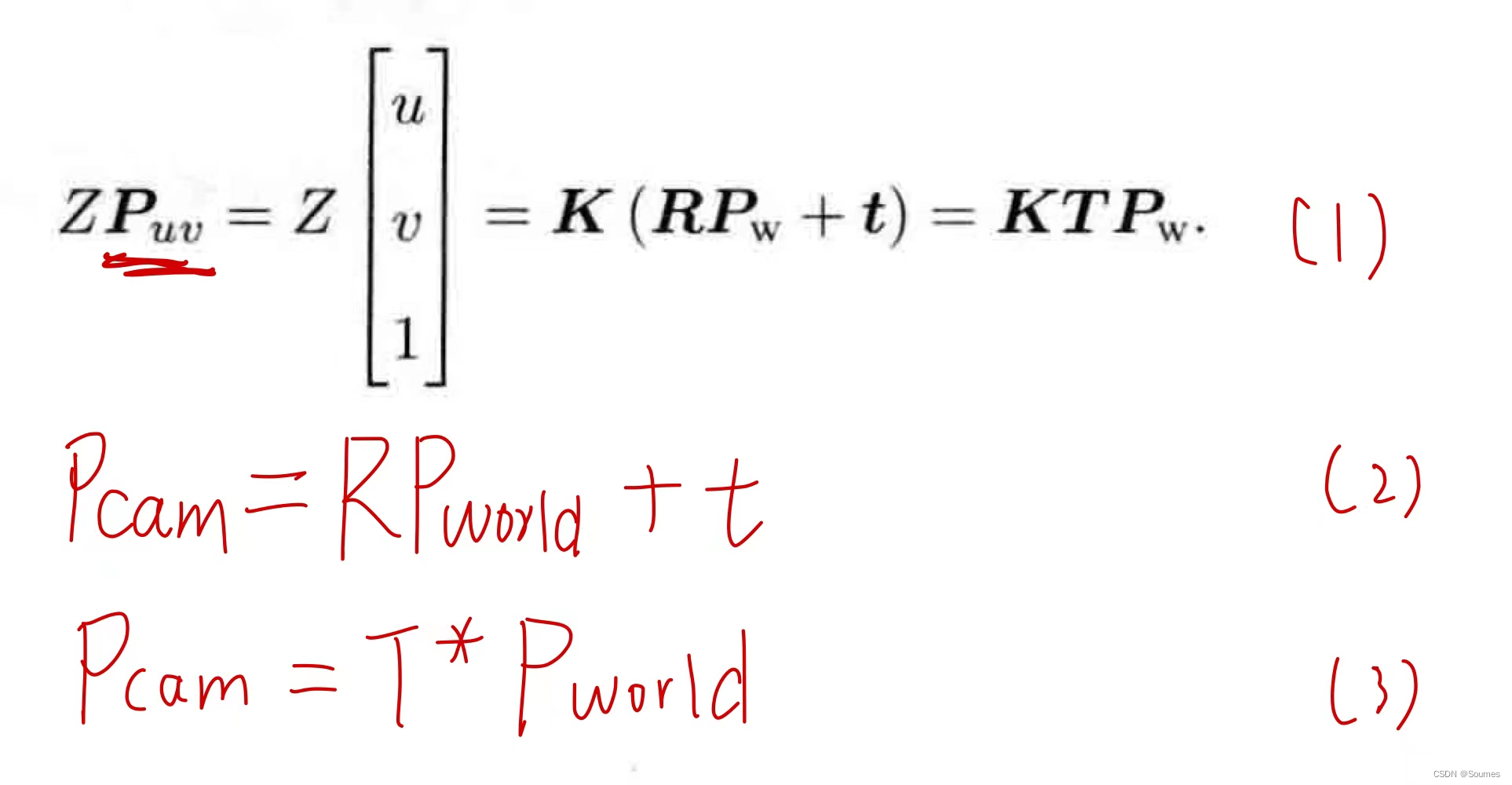
由(2)或者(3)可见,从世界坐标系到相机坐标系需要用到位姿,通过一个估计的位姿将世界坐标P转换到图2的相机坐标系下后,还需要将其转换为像素坐标,这样才算是真正把一个世界坐标点投影到相片上,这个过程的公式可以参考公式(1),通过外参R,t和内参K一步到位,也可以先转换到相机坐标系,再通过下面的公式,将相机坐标转换到像素坐标。
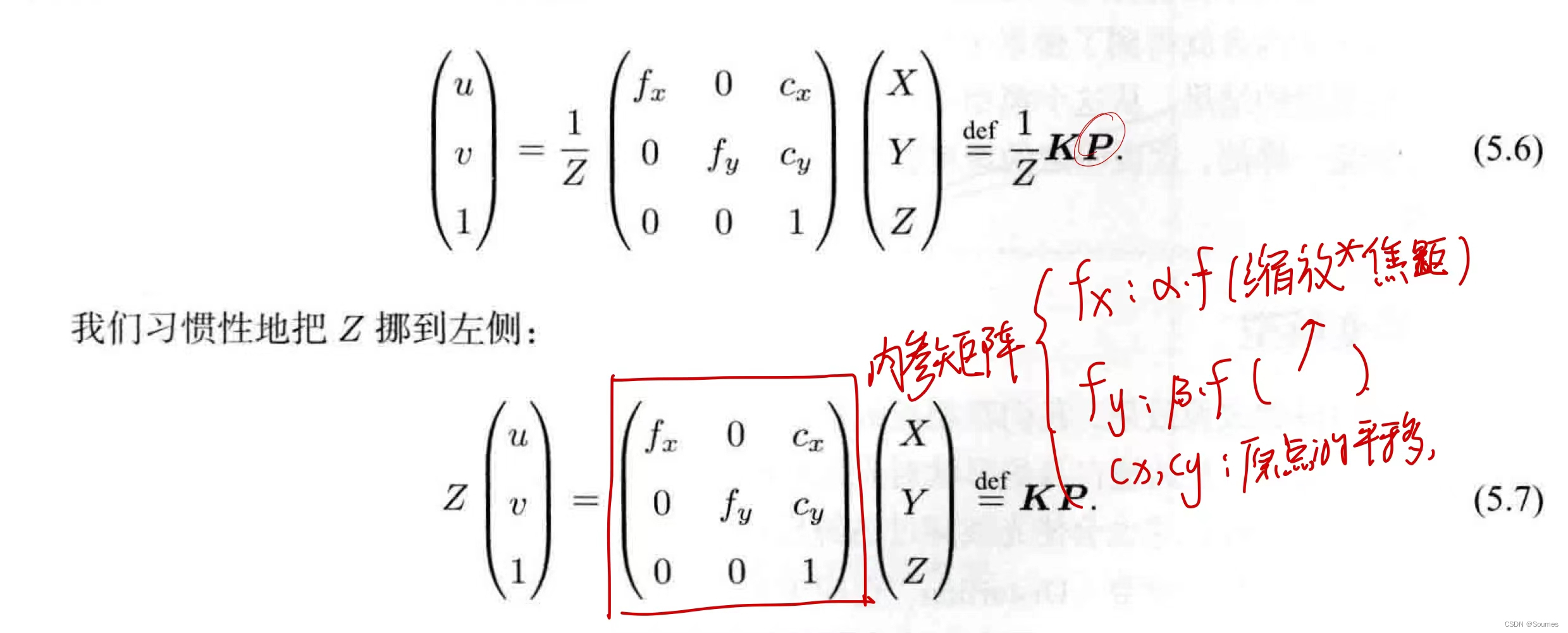
通过这两步转换,我们就得到了草图中P‘的坐标(绿色),这就是P在图2上的投影,P’与P2之间的蓝色连线,就是重投影误差,P2作为观测,是真值,而P’是投影过来的,作为估计值,这两者的差值就是重投影误差所在。这部分对应的代码如下:
//因为此时的坐标是世界坐标,因此要转到相机坐标下
Eigen::Vector3d pc = pose * points_3d[i];//这里用的是世界坐标到相机坐标的公式
//pc就是相机坐标下的三维点
double inv_z = 1.0 / pc[2];//1/Z,在相机转像素用到
double inv_z2 = inv_z * inv_z;//在雅可比计算中才用到
Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);
//再把相机坐标一步到位投影到像素坐标,经历了内参和外参
Eigen::Vector2d e = points_2d[i] - proj;//构建最小二乘方程
cost += e.squaredNorm();//但是误差不能用上面的来描述,用的是平方范数到这里就完成了重投影误差的构建,我们也得到了最小二乘的算式,接下来就可以利用各种方法来求解最小二乘问题了,这里采用高斯牛顿方法求解。
最小二乘的本质实际上就是一个误差函数,这个误差函数和某个待估计值有关,在这里是重投影误差,待估计值是位姿变换T,可以用下面的算式进行描述:

高斯牛顿求解最小二乘的思路,就是寻找一个待估计值的增量,这个增量让待估计值向着使整体误差变小的方向变化,可以用如下算式表示:
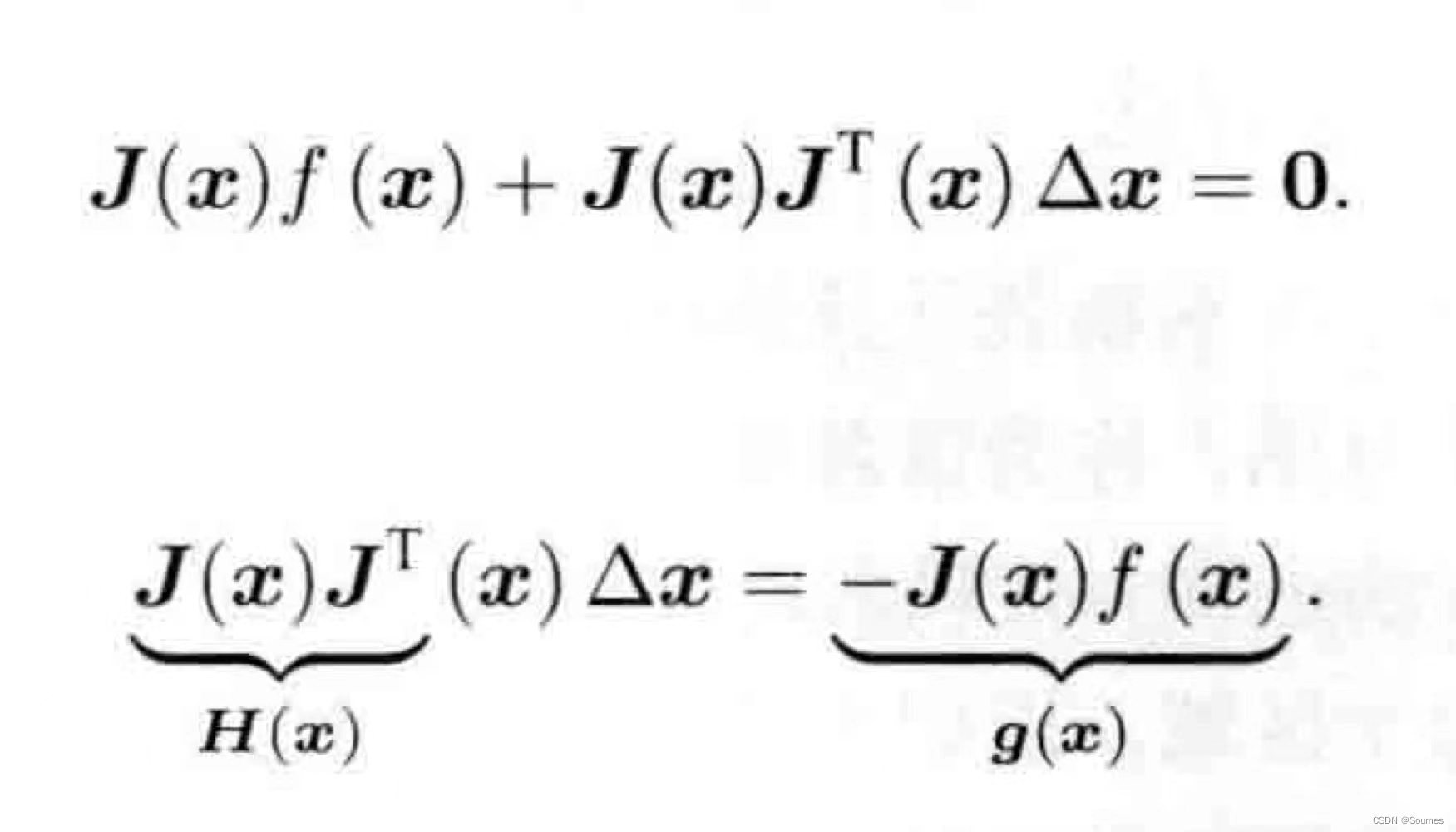
在这个式子中,我们要求解的就是,J(x)是雅可比矩阵,里面存放的是误差函数对于待估计量的偏导数,f(x)就是当前的误差大小,所以在高斯牛顿法中,每次迭代都需要计算雅可比矩阵的大小和f(x)的大小,利用这两个值解出
,然后再用
更新位姿。在这里,雅可比矩阵的式子如下:

这部分的代码如下:
//下面是雅可比矩阵的计算,通过求导推倒出雅可比矩阵,然后把值都代进去算,每个值都是知道的
J << -fx * inv_z,
0,
fx * pc[0] * inv_z2,
fx * pc[0] * pc[1] * inv_z2,
-fx - fx * pc[0] * pc[0] * inv_z2,
fx * pc[1] * inv_z,
0,
-fy * inv_z,
fy * pc[1] * inv_z2,
fy + fy * pc[1] * pc[1] * inv_z2,
-fy * pc[0] * pc[1] * inv_z2,
-fy * pc[0] * inv_z;
//计算海森举证
H += J.transpose() * J;
//计算误差矩阵
b += -J.transpose() * e;
}
Vector6d dx;
//求解dx,dx就是代估计量,在这里就是位姿
dx = H.ldlt().solve(b);//求解用到了海森矩阵和误差矩阵,就是上面求的可见在这里求出了H和b,也就是雅可比矩阵构成的H矩阵和表示f(x)的b,随后利用ldlt算法直接求解dx,最后用dx来更新位姿,就得到了我们所需要的位姿了,代码如下:
pose = Sophus::SE3d::exp(dx) * pose;
lastCost = cost;到此,我们就完成了一个基于优化方法的视觉里程计,输入的是两帧图片和深度,输出的是一个位姿
后续考虑用自己的双目相机跑一下这个程序,然后把位姿轨迹画出来,和真实的轨迹对照一下,看看这个方法好不好用,完成了再继续更新