A fltering algorithm for constraints of difference in CSPs

一. 摘要

Alldierent约束它们在变量子集上由一组元组修饰，在同一元组中出现的值都是不同的。
本文针对这些约束条件提出了一种新的过滤算法。得到了这些非二元约束的广义弧一致性条件。它基于匹配理论，复杂度低。

二.介绍

CSP解的存在性问题是NP完全的。因此，一些方法已经发展起来，以简化CSP之前或期间的搜索解决方案。一致性技术是最常用的技术。对于二进制CSP和N元CSP提出了几种实现弧一致性的算法。
引入的特殊约束的算法AC-4进行了改进，研究了单调和泛函二元约束。在本工作中，我们对n元约束的一个特殊情况：“不同约束”感兴趣，为此我们提出了一个过滤算法。
如果一个约束在变量子集上被一组元组定义，而在同一元组中出现的值都是不同的，则称为“不同约束”。它们存在于现实生活中的许多问题中。
这些约束可以表示为n元约束，并用广义弧一致性算法GAC4进行分层。这种过滤会减少域，但它的复杂性可能会很昂贵。事实上，它取决于所有可容许元组的长度和数目。让我们考虑p个变量的“不同约束”，p个变量的值取自基数D的集合。因此，允许元组的数目对应于从d个元素中选择的p个元素不重复的排列数目：d Pp=d！/（d- p）！ .
因此，一些约束解析系统，用一组二进制约束来表示这些n元约束。在这种情况下，对属于同一“不同约束”的每对变量建立一个不同的的二元约束。
但由于这些约束条件，圆弧一致性的剪枝性能较差。实际上，对于两个变量i和j之间的二元Alldierent约束，只有当j的定义域减少到一个值时，弧一致性才从i的定义域中移除一个值。
让我们假设我们有一个具有3个变量x1，x2，x3和这些变量之间的一个不同约束的CSP（图1）变量的定义域为D 1 = {a, b} , D 2 ={a, b} and D 3 ={a, b,c} . GAC4用一个三元约束表示的不同约束消除了x3域中的a和b值，而用不同的二元约束表示的不同约束的弧一致性不删除任何值。
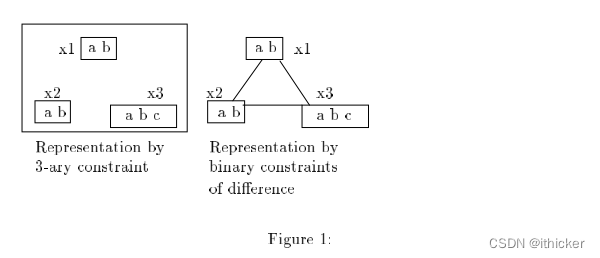
本文给出了一种实现广义弧一致性条件的有效方法，以便从它的剪枝性能上得到更好的结果。其空间复杂度为O(Pd)，时间复杂度为O(P2d2)。

论文的其余部分组织如下。第2节对约束满足问题和匹配问题作了一些初步的探讨，并提出了一种仅涉及约束条件的弧一致性约束表示：双弧一致性。第3节提出了一个新的条件来保证CSPS中的双弧一致性。在第4节中，我们提出了一个ECIANT实现来实现这个条件，并分析了它的复杂性。在第五节中，我们用一个例子说明了它的性能和它的兴趣。第六节给出了结论。

三.准备工作

基本定义

变量x i的域中的值a i与给定的n元约束一致，如果约束中的所有其他变量都存在值使得这些值与a i同时满足该约束。更一般地说，n元CSP的弧一致性或广义弧一致性如下[Mohr和Masini,1988a]

从前面的定义中，我们提出了一个特殊的弧一致性，它只涉及“不同的约束”：

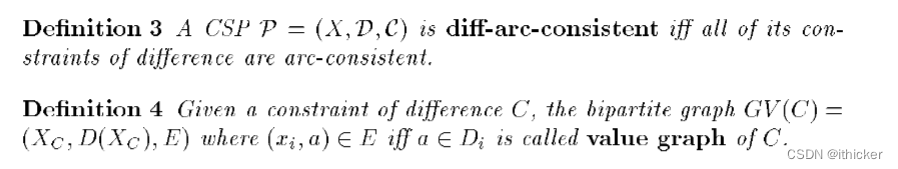
如果X中的每个顶点都是匹配（M）中边的端点，则匹配（M）覆盖集合X。
注意，在二分图G=(X；Y；E）中覆盖X的匹配一定是最大匹配。 （无共同接节点的边集合叫做匹配，那么所有节点一节点对应一个边，一定数量最大，一定四最大匹配）
在下一节中，我们从匹配的定义和值图的定义出发，给出了一个新的必要条件，以保证diff-arc-consistency 在constraints of difference的CSPs上。

四. CSPs具有constraints of difference约束的一个新条件

下面的定理在constraints of difference的值图中建立了diff-arc-consistency 和匹配概念之间的联系。
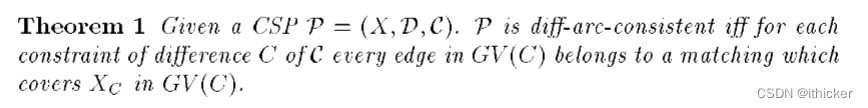
在这里插入图片描述
证明：
=>让我们考虑一个constraints of difference和它的值图GV©的约束。从C的每个可容许元组中，可以建立一组对。对由元组中的变量及其赋值组成。对集包含每个变量的对。这个集合对应于一组边，在GV©中用A表示。由于p是双弧一致的，所以每个元组中的值都是双弧一致的。因此，A的两条边不可能有一个公共顶点，A是覆盖X C的匹配。而且，约束中每个变量的每个值都属于至少一个元组。因此，GV©的每条边都属于覆盖X的匹配
<=
让我们考虑一个变量x i和它的定义域的一个值a。对于constraints of difference C的每一个约束，对（x i,a）都属于GV©中覆盖x c的匹配。由于在匹配中没有两条边有一个共同的顶点，所以约束中的所有其他变量都存在值，使得这些值同时满足约束。所以P是双弧一致的。
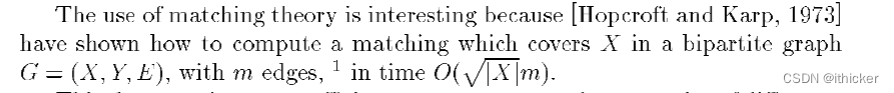
在这里插入图片描述
这个定理给我们提供了一种在CSP中表示constraints of difference 约束的有效方法。实际上，一个constraints of difference 约束只能用它的值图来表示，空间复杂度为O(pd)。它还允许我们给出一个基本的算法（算法1）来过滤一个在其上被constraints of difference约束的集合的变量域。该算法通过建立迭代约束的值图，计算一个覆盖Xc的匹配，以删除所有不属于匹配覆盖Xc的边（delete every edge which belongs to no matching covering Xc）匹配不覆盖。图3给出了这种轻量化的应用程序。
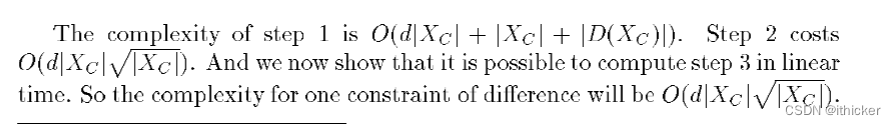
在这里插入图片描述

在这里插入图片描述

五. 删除覆盖X的不匹配边

在这里插入图片描述
为了简化表示法，我们考虑了一个二分图G=(x，y，e）而不是二分图G=(Xc,D(Xc)，e）和一个在G中覆盖X的匹配M。为了理解我们如何删除所有不属于匹配的边（不匹配），我们提出了一些关于匹配理论的定义。欲了解更多信息，读者可以咨询[Berge，1970]或[Lovasz and Plummer，1986]
在这里插入图片描述
一个属于每个最大匹配的边是至关重要的。

图3给出了一个在二分图中覆盖x的匹配示例。粗边是匹配的边。顶点7是自由的。路径（7,x6,6,x5,5）是从自由顶点开始的交替路径。循环（1,x3,3,x2,2,x1,1）是一个交替循环。边缘(x4,4)是至关重要的。

在这里插入图片描述

每个matching序列当中个都有元素（x4,4）因此是vital
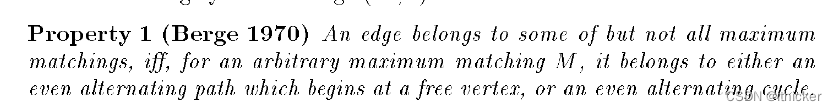
在这里插入图片描述

根据这个性质，我们可以得到一个覆盖X的任意匹配M，每条不属于匹配覆盖X的边（delete every edge which belongs to no matching covering Xc）。有一些边既不属于M（不属于重要），也不属于从自由顶点开始的偶数交替路径，也不属于偶数交替循环。
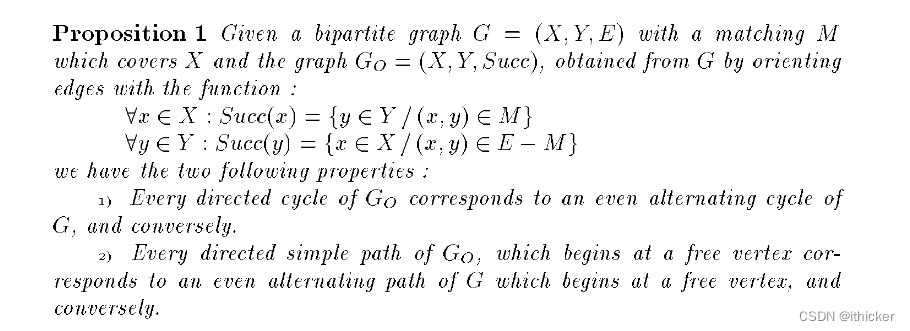
在这里插入图片描述
证明
1）如果我们忽略等价，很明显这个命题是真的。在第一种情况下，由于G是二部的，所以它没有任何奇圈。
2）在第二种情况下，我们必须证明G O的每一条从自由顶点开始的有向简单路径对应于G的一条从自由顶点开始的偶数交替路径。 M是覆盖X的匹配，所以X中没有自由顶点。由于G是二部的，并且由于每条路径都从一个自由顶点开始，所以在Y中，每条奇数有向简单路径都以X中的一个顶点结束。从这个顶点出发，我们总是可以在Y中找到一个不属于该路径的顶点，因为X中的每一个顶点都有一个后继，而Y中的一个顶点都有一个前驱。因此，从一个奇数有向简单路径，我们总是可以建立一个偶数有向简单路径。

从这个命题出发，我们得到了一个线性算法（算法2)，它删除了所有不属于匹配覆盖X的边。（does not belong to any matching which covers X.）
第2步寻找所有属于GO的有向简单路的边，它从一个自由顶点开始。此外，它还得到了一些属于GO的有向圈的边。
步骤3计算GO的强连通分量，因为连接同一强连通分量中两个顶点的边属于有向圈，反之则不属于有向圈。这些边属于G的偶交替圈（cf point 1 of proposition 1）。在这一步之后，属于覆盖X的一些但不是所有匹配的所有边的集合A是已知的。（property1）
G中除去的边的集合Re是:
这是由步骤4完成的。算法复杂度与强连通分量的搜索相同
即对具有m条边和n个顶点的图的O(m+n)。我们给出了对于constraints of difference的一个约束，如何删除覆盖xc的所有不匹配边（o no matching which covers Xc）。 但是，一个变量可能受到多个约束，需要传播删除。事实上，让我们考虑Xi是Xc的一个变量，x i可以受到几个约束。
因此，由于独立于C的原因，可以删除Di的值。该删除涉及从GV©中删除一条边。因此，有必要研究这种GV©调整结构的后果。

六.删除传播

对一个constraints of difference的值的删除可能涉及对其他约束的一些修改。对于constraints of difference的其他约束，我们可以利用删除前已知覆盖X的匹配这一事实来做得比重复第一个算法更好。
我们提出的传播算法有两组集合作为参数。第一个表示要从二分图中删除的边集，第二个表示要通过过滤删除的边集。该算法需要一个用MatchingCoveringX（G，M1，M2)表示的函数，该函数从一个不是最大值的匹配M1中计算出一个覆盖X的匹配M2。如果M2存在，则返回true，否则返回false。新的过滤由算法3表示。
全文共分为三个部分。首先，它从二分图中去除边。其次，它最终计算一个覆盖Xc的新匹配。第三，删除不属于任何匹配覆盖Xc的边。如果ER包含重要边或不存在覆盖Xc的匹配，则该算法返回false
现在，让我们来计算它的复杂性。设M为G的边数，N为顶点数。假设我们必须从中去掉K条边G (|ER| = k).。算法 1的复杂度在O(k)中。在最坏的情况下，步骤2包括从基数|M-K|的匹配计算匹配覆盖Xc。这种计算的代价是O（根号K乘M）（参见[Hopcroft and Karp，1973])。步骤3的复杂度为O(m)。
在最坏的情况下，G的边可以一条一条地删除。那么前一个函数将被调用m次。因此全局复杂性在O(M2)中。若p=|Xc|且d是x c的变量域的最大基数，则对于一个constraints of difference约束，复杂度为O(p2d2)。

六. 一个例子：斑马问题

那里有5个房子，每个房子都有一个明亮的颜色，住着不同国籍的男人，有宠物，饮料和香烟。
英国人住在红房子里。
西班牙人养了一只狗。
Coee在绿色房子喝醉了
乌克兰人喝茶
绿色的房子就在象牙色房子的右边。
老金烟鬼拥有蜗牛
在黄色的房子里，库尔斯正在被熏
Milk在中间的房子里喝。
挪威人住在左边的第一个房子里
切斯特尔德吸烟者住在狐狸主人旁边
库尔斯在养马的房子旁边的房子里被熏。
幸运的吸烟者喝橙汁
日本人吸烟议会
挪威人住在蓝房子旁边。
问题是：谁喝水，谁拥有斑马？

这个问题可以表示为一个包含25个变量的约束网络，每个变量对应5个颜色、饮料、国籍、香烟和宠物：

每个变量具有域值{1，2， 3， 4，5}，每个数字对应一个房子位置（例如将值2赋给可变马意味着马主人住在第二个房子里）[Dechter，1990]。断言2到15被转换为一元和二元约束。此外，有三种表示第一个断言的方法，这意味着同一集群中（颜色、饮料、国籍、香烟和宠物）的变量必须采用不同值：

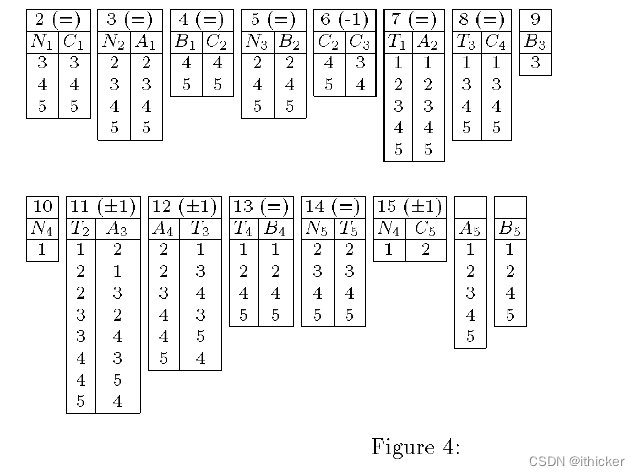
第一种表示法通常被用来解决这个问题[Dechter，1990；Bessiere和Cordier，1993]。从这三种表示形式出发，我们可以研究弧相合的一些结果。它们在图4和5中给出。对应于断言2到15的约束在扩展中表示。为了清楚起见，省略了各聚类变量之间的不确定性约束。

对于第一种表示，在图4中给出了圆弧相合化的结果。
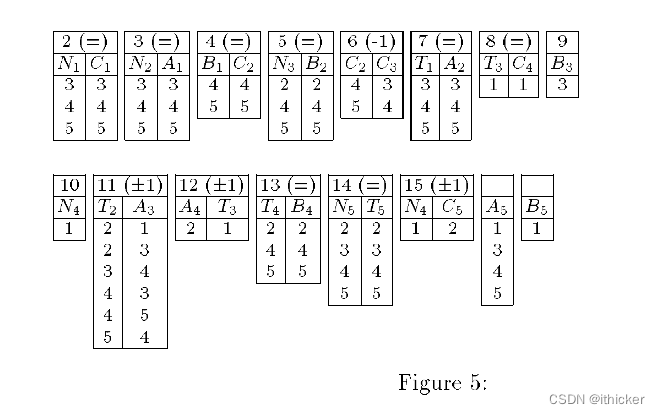
对于第二种表示，采用了广义弧相合算法。图5显示了新的结果。它修剪了比上一个更多的值。
对于第三种表示，对二元约束采用圆弧一致性算法，并结合对二元约束采用新的迭代算法。所得结果与第二种方法相同。

让我们用与断言2到15相对应的二进制约束的数目来表示，p表示一个簇的大小，c表示簇的数目，d表示一个域中的值的数目，o(ed2)表示二进制CSPs中弧一致性2的复杂度。让我们计算这三种方法的复杂性：

第二个轻量化消除了比第一个更多的值。但它的复杂性更高。本文提出的表示和算法给出了与第二种方法相当的剪枝结果，其复杂度与第一个方法相同。因此，我们可以得出结论，新的过滤是好的来解决问题即看起来像斑马的问题。

七. 结论

本文给出了CSPS中的一种离散约束的过滤算法。该算法可以看作是实现一类特殊约束&离散约束的广义弧一致性条件的一种有效方法。它使我们能够以较低的复杂度从前面条件的剪枝性能中获得提高。实际上，对于一个约束条件，其空间复杂度为O(Pd)，时间复杂度为O(P2，d2)。它已经被证明对斑马问题非常有效。并成功地用于复杂有机合成方案的计算机辅助设计系统Resyn[Vismara et al.，1992]中的子图同构问题的求解。