柱面拟合
一、背景
这篇文章是用于通过测量柱面上一些三维点建立方程求解柱面方程,源于python库py_cylinder_fitting,相识于GTE,终于《Least Squares Fitting of Data by Linear or Quadratic
Structures》。
二、圆柱的表达式
无限圆柱由一个包含点C和过点的单位长度方向为W的轴指定。圆柱的半径为r > 0。设右手标准正交集{
U,V,W},即U,V,W相互垂直,向量积表示为U × V = W,V × W = U,W × U = V,单位向量U · U = V · V = 1,则任意点X都可以表示为
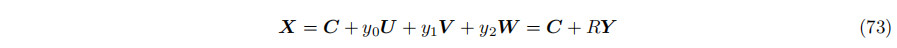
其中,R是一个旋转矩阵,其列是U、V和W,其中Y是一个列向量,其行是y0、y1和y2。在圆柱上,则
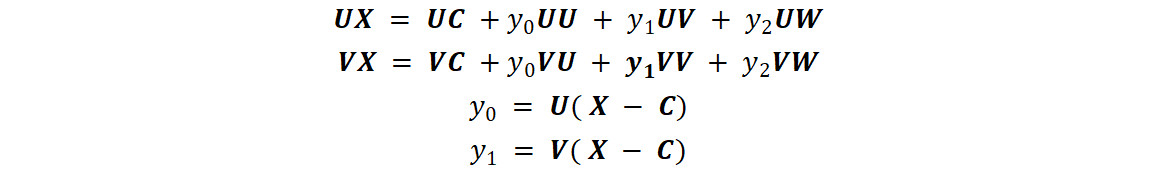
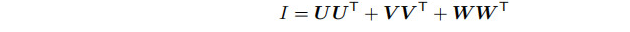
得半径

在有限圆柱上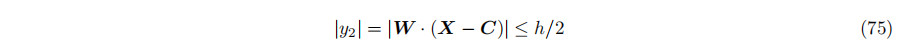
二、最小二乘法损失函数
另输入点集合为{ Xi},基于公式74得到得圆柱误差函数为
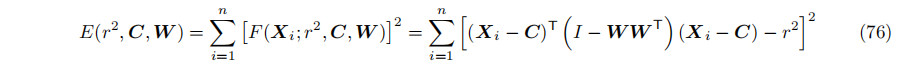
公式里有6个待求参数,分别是1个半径r、点C的3个坐标和W的两个方向向量
为了提高数值计算的稳健性和减少数值计算的误差,我们从样本中减去样本均值,这种方法通常被称为"零均值化"或"中心化"。接下来,设
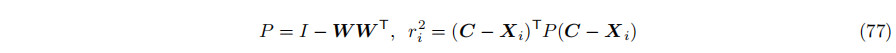
这里矩阵P表示在W平面上的投影,因此P^2 = P只依赖于方向W。半径ri^2取决于中心C和方向W。误差函数简洁地写成如下形式
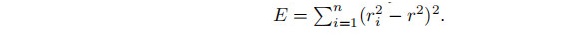
三、半径方程式
将误差函数相对于平方半径的偏导数设置为零,我们就有了约束条件
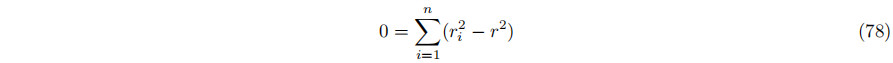
相当于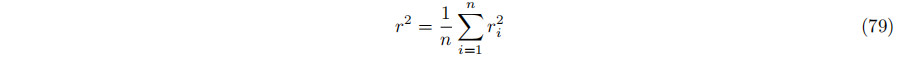
平方半径是Xi−C在包含C和具有正态W的平面上的投影的平方距离的平均值,取决于C和W。
如果以下等式成立

则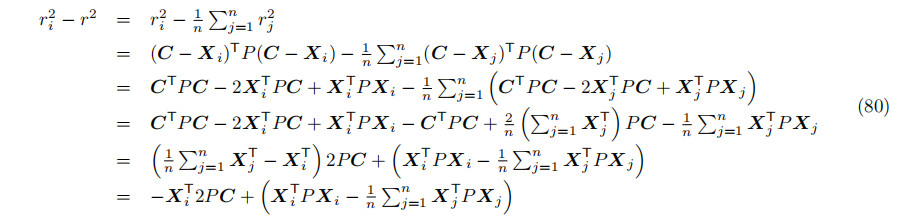
四、中心方程式
将误差函数相对于中心的偏导数设置为零
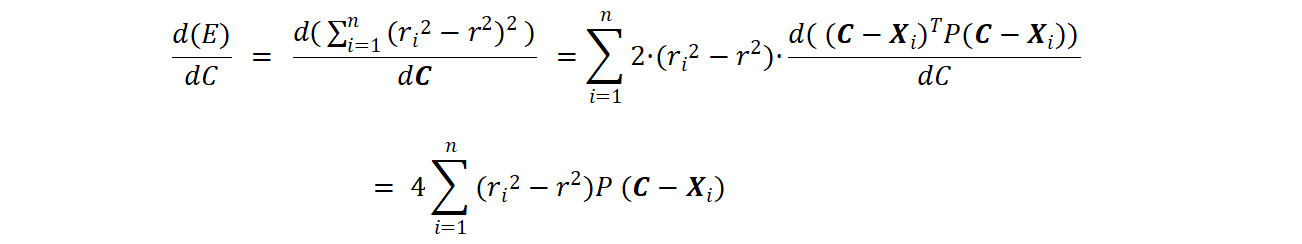
结合公式78,我们就有了约束条件
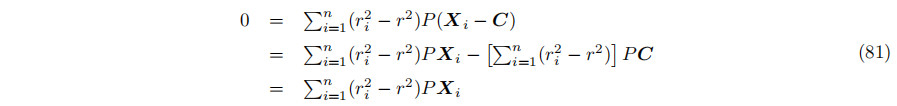
将公式80乘PXi的总和,使用公式81得到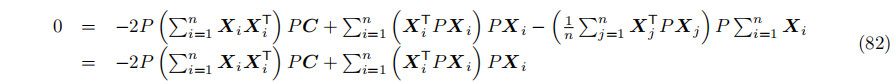
C + tW是所有t的有效中心,只要计算出一个没有分量的中心就足够了在w方向;也就是说,我们可以构造一个点,其中C = PC。它足以求解PC的方程(82)写成线性系统A(PC)= B/2
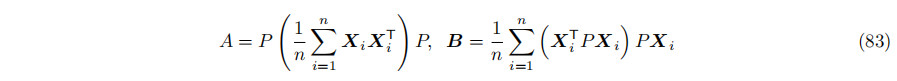
投影矩阵是对称的P = PT ,引入P = P2,则XiT P Xi = XiT P2 Xi = XiT PT P**Xi**
矩阵A是奇异的,因为投影矩阵P是奇异的,所以我们不能直接反转A来求解方程。线性系统涉及的项只存在于垂直于W的平面上,所以实际上线性系统在投影空间中简化为两个未知数的方程,只要系数矩阵是可逆的,它是可解的。
选择U和V,使{
U、V、W}是一个右手标准正交集;然后是PXi =µiU+νiV和PC = k0U + k1V,其中µi=U·Xi、νi = V·Xi、k0 = U·PC和k1 = V·PC。矩阵A变成了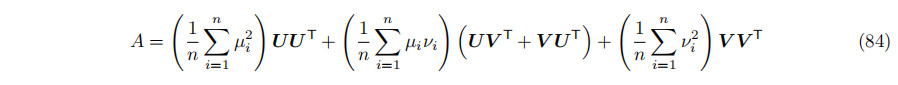
向量B就变成了
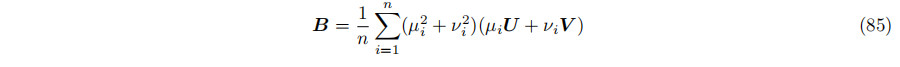
向量A(PC)就变成了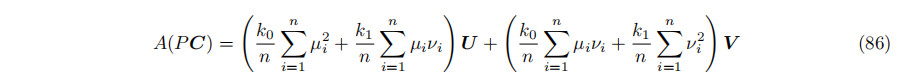
将其等于B/2,并将U和V的系数分组,得到线性系统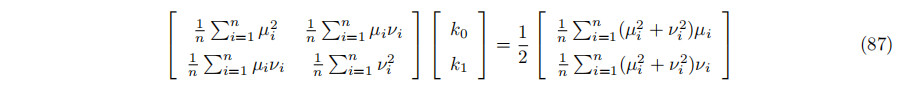
系数矩阵是样本在垂直于W的平面上的投影的协方差矩阵。直观地说,只要投影不在一条直线上,该矩阵是可逆的。如果矩阵是奇异的(或在数值上几乎是奇异的),则原始样本是在一个平面上(或在数值上几乎是在一个平面上)。它们不能很好地用一个圆柱体安装,或者说它们不能用一个无限半径的圆柱体安装。
方程(87)的矩阵体系的解为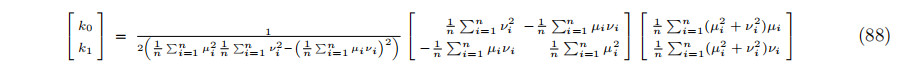
这样就得到了圆柱体中心PC = k0U + k1V;在公式(74)中用这个来代替C。
虽然解决方案似乎取决于U和V的选择,但它不是。设W =(w0、w1、w2),并定义斜对称矩阵
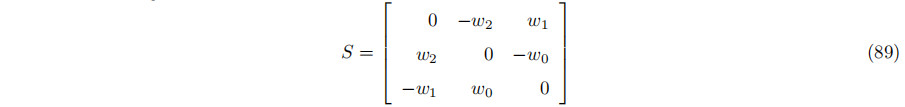
根据倾斜对称的定义,ST =−S。这个矩阵表示任何向量ξ的交叉积运算: Sξ = W×ξ。因为{
U,V ,W}是一个右交标准正交集,所以它遵循SU = V和SV =−U。它还可以显示,S = VUT−UVT。定义矩阵Aˆ为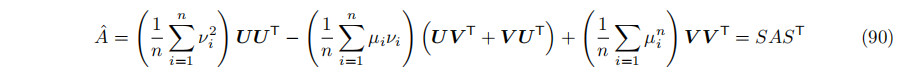
实际上,这生成了一个2×2矩阵,它是表示A的2×2矩阵的辅助器。它具有属性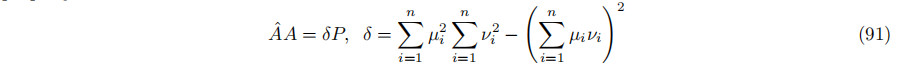
一个矩阵的轨迹是对角线项的和。观察到跟踪§ = 2,因为|W| 2 = 1。通过对AˆA=δP的跟踪,我们得到了2δ = Trace(AˆA)。圆柱体中心是通过将A(PC)= B/2乘以Aˆ得到的,使用公式(83)中的定义和公式(91),
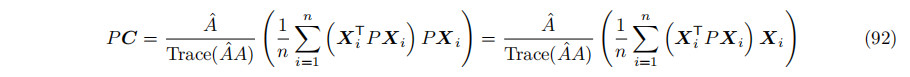
其中,最后一个等式使用AˆP=Aˆ,因为STP = ST。方程(92)独立于U和V,但依赖于W。
五、方向方程式
让方向参数化为W(s) =(w0(s),w1(s)、w2(s)),其中s是一个二维参数。例如,球坐标是这样一个参数化:W =(cos s0 sin s1,sin s0 sin s1,cos s1),s0∈[0,2π)和s1∈[0,π/2],其中w2(s0,s1)≥0。E的偏导数是
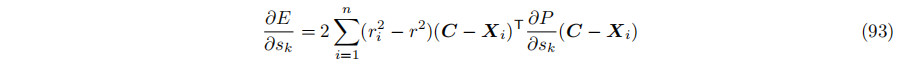
以封闭形式求解∂E/∂sk=0是难以处理的。可以在W的分量中生成一个多项式方程组,利用消去理论得到一个变量中的多项式,然后找到它的根。这种方法通常很乏味,而且在数值上也不健壮。
或者,我们可以跳过∂E/∂sk=0的根查找,而不是将方程(80)和(92)直接输入误差函数E/n = 1 n P n i=1(ri 2−r 2)2,得到一个非负函数,
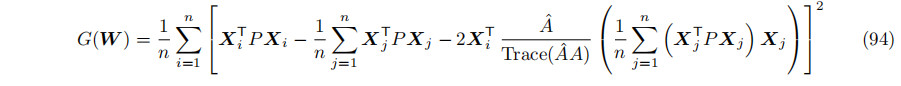
可以采用一种定位G的最小值的数值算法。或者,如示例代码中所示,(s0,s1)的域可以被划分为被用来计算G的样本。产生最小G值的样本决定了一个合理的方向w。中心C和平方半径r2是在G的评价中固有的,所以最终我们有一个拟合的圆柱体。对于大量的样本来说,G的计算是昂贵的:方程(94)包含一个项的和,然后是平方,然后是另一个和。
一些代数操作导致封装和,允许我们预先计算和,并将G (W)表示为w分量的有理多项式。这种方法提高了CPU上的性能。它还允许在GPU上实现大规模并行性能的有效实现——从一个半球采样的一个方向向量有一个GPU线程。投影矩阵P由其上三角元素p =(p00、p01、p02、p11、p12、p22)决定。我们可以写在下面,其中p被表示为一个6×1向量,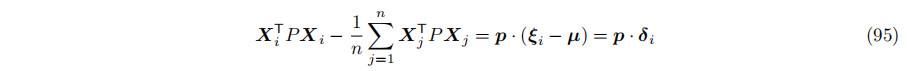
接下来定义了6个×1向量ξi、µ和δi(写为6个元组)。作为一个3元组,让西=(西,一,子)
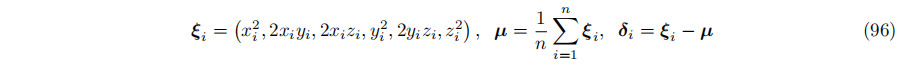
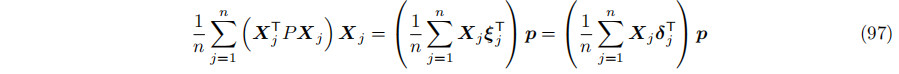
最后一个等式是真的,因为P n j=1 Xj = 0意味着P n j=1 XjµT = 0。阐明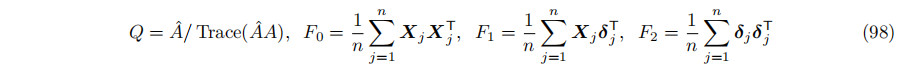
其中,Q和F0为3×3,F1为3×6,F2为6×6;然后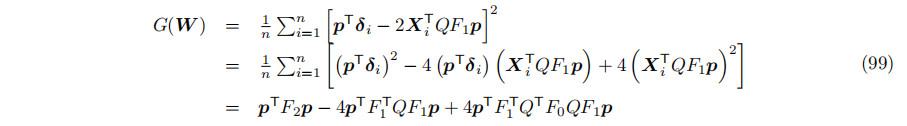
对输入样本{Yi} n i=1的预计算如下依次计算。这些步骤与方向向量W无关。
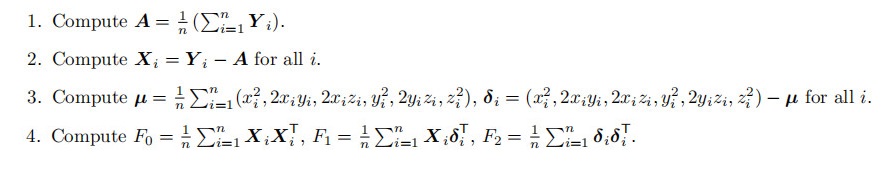
对于每个指定的方向W,依次执行以下步骤。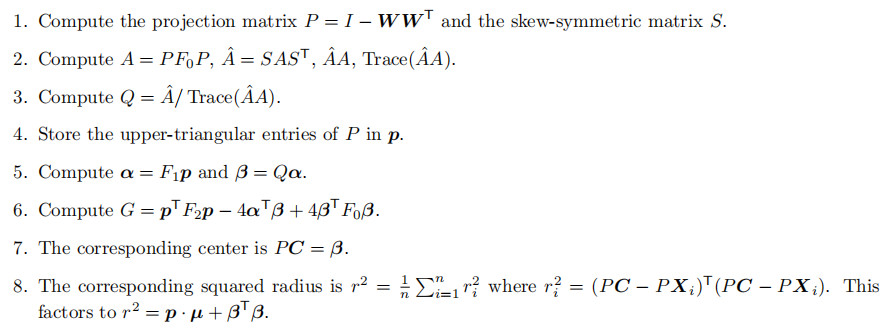
六、整体流程
首先求方向向量W,再求点P,最后求r2,
预处理伪代码如下:
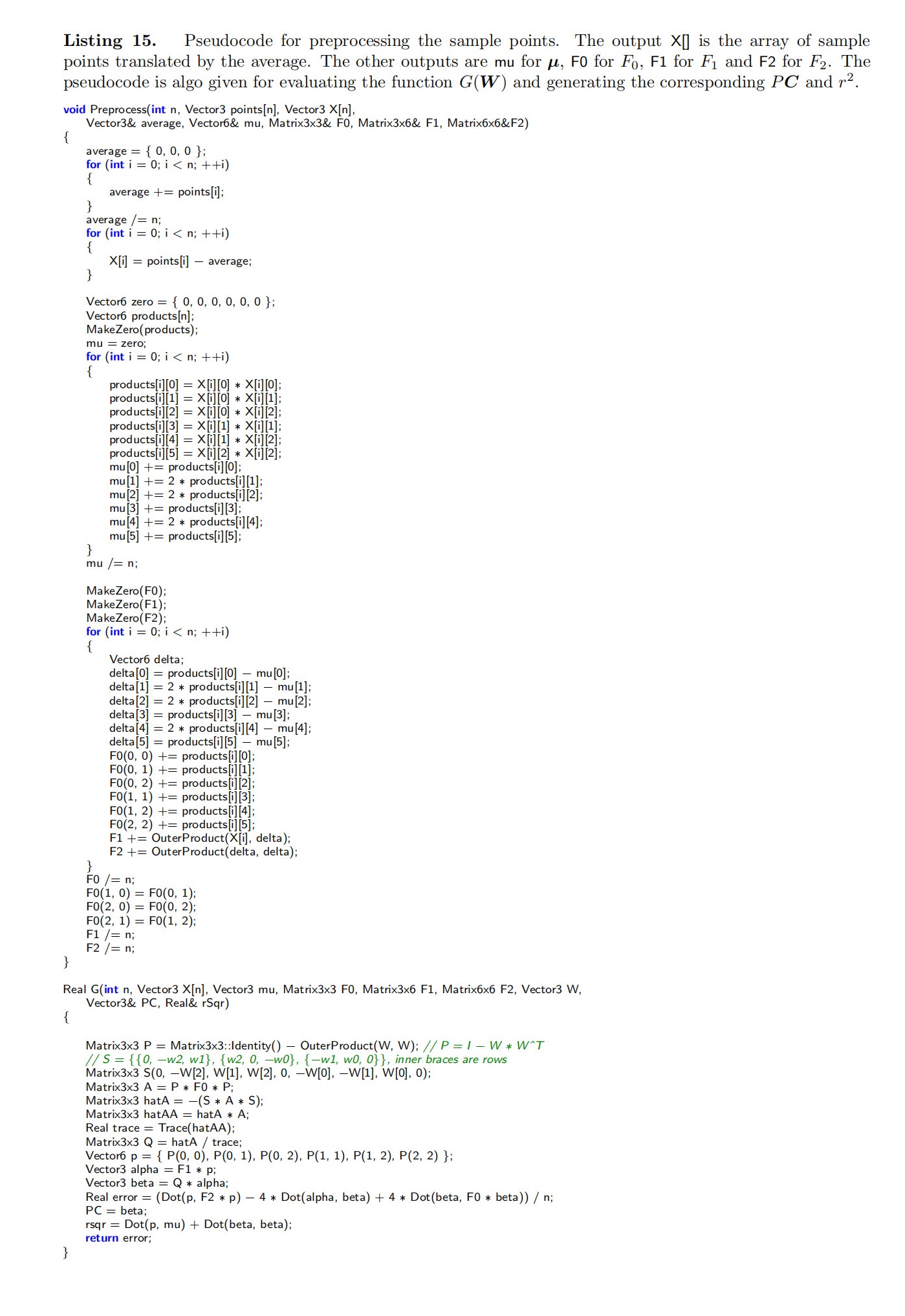
求解如下:
