关系代数
关系代数是通过对关系的运算来表达查询的。它的运算对象是关系,运算结果也是关系。
关系代数的五个基本运算
(1)并(∪)
R∪S≡{t∣t∈R∨t∈S},t为元组变量,R和S结构相同。
其含义为: 任取元组t,当且仅当t属于R或t属于S时,t属于R∪S。 R∪S是一个n目关系。
(2)差(-)
R-S≡{t∣t∈R∧t∉S},t为元组变量,R和S结构相同。
其含义为: 当且仅当t属于R并且不属于S时,t属于R-S。 R-S也是一个n目关系。
(3)笛卡尔积(Χ)
用一个关系的每一行与另一个关系的所有行拼接起来,最后得到的关系的行数等于原来两个关系行数的积
RΧS≡{t∣t=〈tr,ts〉∧tr∈R∧ts∈S}
(4)投影(Π)
对一个关系进行垂直分割,消去某些列,并重新安排列的顺序,再删去重复元组。
Πi1,…,im(R)≡{t∣t=〈ti1,…,tim〉∧〈t1,…,tk〉∈R}
(5)选择(σ)
根据某些条件对关系做水平分割,选择符合条件的元组。
σF(R) ≡{t∣t∈R∧F(t)∈true}
关系的四个组合操作
(1)交
设关系R和关系S具有相同的元数n(即两个关系都有n个属性),而且相应的属性取自同一个域。关系R和S的交记为R∩S,结果仍为n元的关系。由即属于R又属于S的元组组成。
R∩S≡{t︱t∈R∧t∈S}
R∩S≡R-(R-S) 或R∩S≡S-(S-R)
(2)联接
联接操作是笛卡儿积、选择操作的组合。
其中A是R的属性,B是S的属性。
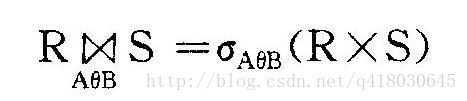
如果θ为等号“=”,那么这个联结操作称为等值连接。
(3)自然联接
将关系R和S中公共属性组满足对应分量相等的元组联接起来, 并且要在结果中把重复的属性去掉。
R⋈S≡Π去掉S中公共属性(σ公共属性上值相等(RΧS))
(4)除
设关系R和S的元数分别为:r、s(r>s>0),
R÷S: 是一个(r-s)元的元组的集合,
是满足下列条件的最大关系:
其中每个元组t与S中每个元组u组成的
新元组必在关系R中。
除运算快速计算的方法:R减去与S中相等的列名的列,剩下的列名就是结果列中的列名。根据结果列的元组值进行分组,判断这些组是否包含有S,如果包含,则是最后得到结果的元组值
关系的三个扩充操作
(1)外联接 
在R和S做自然联接时,把原该舍弃的元组也保留在新关系中,同时在这些元组新增加的属性上填上空值(null),这种操作称为“外联接”操作
(2)外部并
如果R和S的关系模式不同,构成的新关系属性有R和S的所有属性组成(公共属性只取一次),新关系的元组由属于R或属于S的元组构成,同时元组在新增加的属性上填上空值
(3)半联接
关系R和S的半联接操作记为R ⋉ S:
R和S的自然联接在关系R的属性集上的投影
即: R ⋉ S ≡ πR(R ⋈ S)
关系演算
元组关系演算
元组表达形式{ t∣P(t)},t为元组变量,P(t)是由原子公式和运算符组成的。表示满足公式P的所有元组t的集合。
原子公式有三类:
(1) R(t)
R为关系名,意为t是R中的一个元组。{t|R(t)}意为,任取t,只要t是R中的一个元组,t就是结果中的一个元组。{t|R(t)}即表示关系R。
(2)t[i]θu[j]
t和u都是元组变量,θ是比较比较符。 公式表示t 的第i个分量和u的第j个分量满足比较关系θ,则t为结果关系中的元组。
如{t|R(t)∧t[5]>t[3]},意为: 对于R中的任一元组,当且仅当其第5列属性值大于第3列属性值时,它就是结果关系的一员。
(3)t[i]θC或Cθt[i]
C为常数。 表示t的第i个分量与常数C之间满足θ比较符时,t为结果关系中的元组。 如{t|R(t)∧t[7]=‘01’},意为: 对R中的元组,当且仅当其第7列属性值为‘01’时,它就是结果关系中的一个元组。
公式的完整定义:
在一个公式中,如果一个元组变量的前面没有存在量词或全称量词的符号定义,称之为自由元组变量,否则称为约束元组变量。
原子公式的完整定义如下:
(1) 单个原子公式是公式。
(2) 若P1和P2是公式,则P1∧P2、 P1∨P2、┒P1也是公式。
(3) 若φ是公式,则彐(ti)φ也是公式。其中,i=1,2,…,k。
(4) 若φ是公式,则∀(ti)φ也是公式。其中,i=1,2,…,k。
用元组关系演算表达式来表示关系代数的五种基本运算:
并R∪S={ t∣R(t)∨S(t)}
差R-S={ t∣R(t)∧┓S(t)}
笛卡尔积RΧS={t∣(彐u)(彐v)(R(u) ∧S(v) ∧t[1]=u[1] ∧…∧t[n]=u[n] ∧t[n+1]=v[1] ∧…∧t[n+m]=v[m])}
投影Πi1,…,ik(R)={t∣( 彐u)(R(u) ∧t[1]=u[i1] ∧…∧t[k]=u[ik])}
选择σF(R) ={t∣R(t)∧F’ }
在公式中,各种运算符的优先次序为:
(1)算术比较运算符
(2)量词次之
(3)逻辑运算符最低,且┒的优先级高于∧和∨的优先级
(4)加括号时,括号中运算符优先,统一括号内的运算符的优先级遵循(1)(2)(3)
三个等价转换规则:
(1)P1∧P2等价于┒(┒P1∨┒P2);P1∨P2等价于┒(┒P1∧┒P2)
(2)(∀s)(P1(s))等价于┒(彐s)(P1(s));(彐s)(P1(s))等价于┒(∀s)(┒P1(s))
(3)P1=>P2等价于┒P1∨P2
域关系演算
域关系演算类似于元组关系演算,不同之处是用域变量代替元组变量的每一个分量,域变量的变化范围是某个值域而不是一个关系。
原子公式有两种形式:
(1)R(t1…tk):R是K元关系,每个ti是域变量或常量。
(2)xθy,其中x,y是域变量或常量,但至少有一个是域变量,θ是算术比较运算符。
域关系演算的公式中也可使用∧、∨、┒和=>等逻辑运算符也可用(彐x)和(∀x)形成新的公式,但变量x是域变量,不是元组变量。
自由域变量、约束域变量等概念和元组演算中一样
例:R1={XYZ∣R(XYZ)∧Z<8∧X=d}
元组表达式到域表达式的转换
(1)对于k元的元组变量t,可引入k个域变量t1…tk,在公式中t用t1…tk替换,元组分量t[i]用ti替换
(2)对于每个量词(彐u)或(∀u),若u是m元的元组变量,则引入m个新的域变量u1…um。在量词的辖域内,u用u1…um替换,u[i]用ui替换,(彐u)用(彐u1)…(彐um)替换,(∀u)用(∀u1)…(∀um)替换
例:{w|(彐u)(彐v)(R(u)∧S(v)∧u[2]=v[1]∧w[1]=u[1]∧w[2]=v[2])
}这个元组关系可以用上述方法转换为域表达关系:
{w1w2|(彐u1)(彐u2)(彐v1)(彐v2)(R(u1u2)∧S(v1v2)∧u2=v1∧w1=u1∧w2=v2)},
再进一步简化得{w1w2|(彐u2)(R(w1u2)∧S(u2w2))}
用域关系演算表达式来表示关系代数的五种基本运算:
并R∪S={ t1,…,tk∣R(t1,…,tk)∨S(t1,…,tk)}
差R-S={ t1,…,tk∣R(t1,…,tk)∧┓S(t1,…,tk)}
笛卡尔积RΧS={ t1,…,tn ,…,tn+m∣( u1…un)(v1…vm)(R(u1…un) ∧S(v1…vm) ∧t1=u1∧… ∧tn=un∧tn+1=v1 ∧…∧tn+m=vm)}
投影Πi1,…,ik(R)={ t1,…,tk∣( u1…un)(R(u1…un) ∧t1=ui1 ∧…∧tk=uik)}
选择σF(R) ={t1,…,tk∣R(t1,…,tk)∧F’ }
关系运算的安全性和等价性
任何一个有限关系上的关系代数操作结果都不会导致无限关系和无穷验证,所以关系代数系统总是安全的。然而元组关系演算系统和域关系演算系统可能产生无限关系和无穷验证。
无限关系(指元组个数为无穷多个的关系)
无穷验证(验证公式真假时需要进行无限次验证)
我们约定,运算只对表达式中公式设计到的关系值范围内的变量进行操作,这样就不会产生无限关系和无穷次验证的问题,关系演算才是安全的。
关系运算的等价性:
并、交、笛卡尔积、投影、选择运算是关系代数最基本的运算,构成了关系代数运算的最小完备集。在这基础上,关系代数、安全的元组关系演算、安全的域关系演算在关系的表达和操作能力上是完全等价的。它们典型的代表是ISBL语言、QUEL语言、QBE语言。
SQL语言是介于关系代数和关系演算之间的一种关系查询语言。
查询优化
在关系代数表达式中,由于操作次序的不同而执行效率差别很大,那么怎样的操作次序执行起来既省时间,又省空间,这就是优化问题。
关系代数表达式的等价变换规则
(1)联接和笛卡尔积的交换律
如下
(2)联接和笛卡尔积的结合律
如下
设E1和E2是两个关系代数表达式,F是连接运算的条件,则

(3)投影的串接
设E是一个关系代数表达式,A1,A2,…,An是属性名,并且Bi∈{A1,A2,…,An}(i=1,2,…,n),则
∏B1,B2,…,Bm(∏A1,A2,…,An(E))≡∏B1,B2,…,Bm(E)
(4)选择的串接
设E是一个关系代数表达式,F1和F2是两个选择条件,则 σF1(σF2(E))≡σF1∧F2(E)
本规则说明,选择条件可合并成一次处理。
(5)选择和投影操作的交换
此条比较重要,之后画优化树必备等价交换规则
设E为一个关系代数表达式,选择条件F只涉及属性A1,A2,…,An,
则σF(∏A1,A2,…,An(E))≡∏A1,A2,…,An(σF(E))
若上式中F还涉及不属于A1,A2,…,An的属性集B1,B2,…,Bm,则有
∏A1,A2,…,An(σF(E))≡∏A1,A2,…,An(σF(∏A1,A2,…,An,B1,B2,…,Bm(E)))
主要关注后面部分,等于先把我们需要的列投影后,在选择出满足关系的元组,最后选择出结果列。为什么要这么做,之后总结优化树的时候会介绍
(6)选择对笛卡尔积的分配律
设E1和E2是两个关系代数表达式,若条件F只涉及E1的属性,则有 σF(E1×E2)≡σF(E1)×E2
若有F=F1∧F2,并且F1只涉及E1中的属性,F2只涉及E2中的属性,则 σF(E1×E2)≡σF1(E1)×σF2(E2)
若F1只涉及E1中的属性,F2却涉及了E1和E2两者的属性,则有 σF(E1×E2)≡σF2(σF1(E1)×E2)
及早地执行选择操作是重要的操作规则。可以减少做笛卡尔积的行数从而优化关系代数
(7)选择对并的分配律
同(6)
(8)选择对集合差的分配律
同(6)
(9)选择对自然联接的分配律
同(6)
(10)投影对笛卡尔积的分配律
∏L1∪L2(E1XE2)≡∏L1(E1)X∏L2(E2)
其中L1是E1中的属性集,L2是E2中的属性集
(11)投影对并的分配律
同(10)
优化的一般策略
(1)在关系代数表达式中尽可能早地执行选择操作(最基本的,使得中间的结果显著变小)
(2)把笛卡尔积和其后的选择操作合并成F联接运算
(3)同时计算一连串的选择和投影操作,以免分开运算造成多次扫描文件(这里和优化树有很大的区别)
(4)如果在一个表达式中多次出现某个子表达式,那么应该将该子表达式预先计算出结果保存起来,以免重复计算
(5)适当地对关系文件进行预处理
(6)在计算表达式前应先估计一下怎么计算合算
优化算法(画优化树)
利用等价变换规则,使优化后的表达式能遵循一般原则。 这就是优化算法的工作。
(1)利用规则4,把形如σF1∧F2∧…∧Fn(E)的内容变换为 σF1(σF2(…σFn(E)…))
(2)对于每一个选择,使用规则4至规则8,尽可能把它移到树的叶端(即尽可能使它早一点执行)。
(3)对每一个投影,利用规则3,5,9,10,把它尽可能移向树的叶端。 使用规则3可能会消去一些投影,使用规则5可能把一个投影分成两个,其中一个有可能被移向树的叶端。
(4)利用规则3,4,5把选择和投影串接成单个选择、 单个投影或一个选择后跟一个投影,使多个选择或投影能同时执行或在一次投影中同时完成。(这里就提到了用之前强调的规则5进行,有投影+选择都要变成投影+选择+投影)
(5)生成一个程序,每一组结点的计算是程序中的第一步,各步的顺序是任意的只要保证任何一组不会再它的子孙组之前计算
例:“检索选修LIU老师所教课程的女学生的学号和姓名”
πSNO,SNAME(σTNAME =‘LIU’∧SEX =‘F’(S⋈SC⋈C))
该表达式的语法树为:
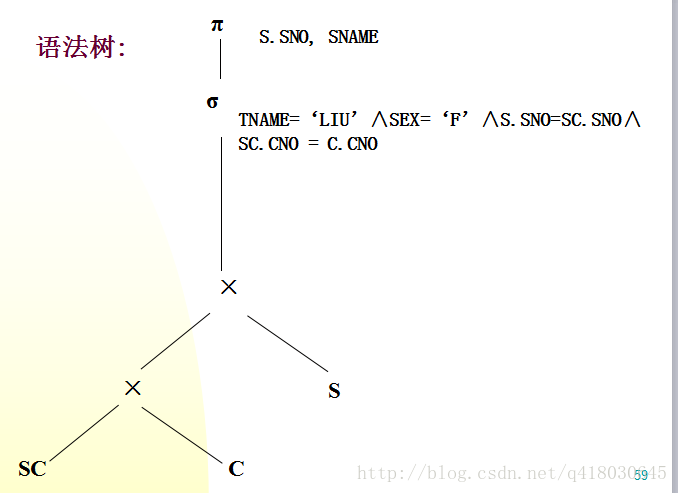
将每个选择操作尽可能的靠近树的叶端:
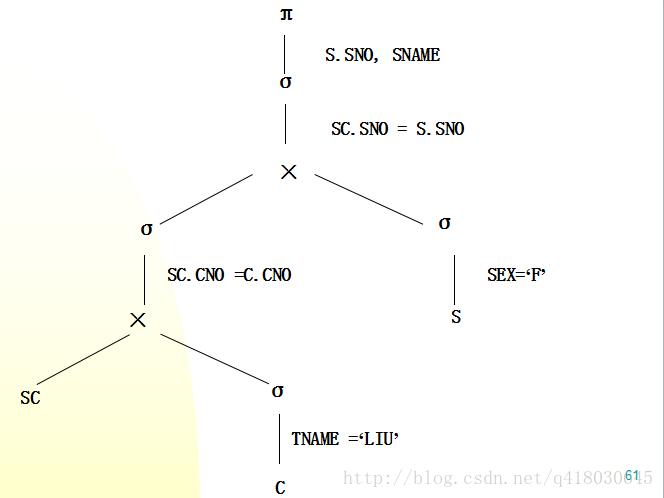
然后使用规则5
关系代数表达式的运用技巧
(1)对于只涉及到选择、投影、联接的查询可用下列表达式表示:
π…(σ…(R×S)) 或者 π…(σ…(R⋈S))
(2)对于否定的操作,一般要用差操作表示
例如: “检索不学C2课的学生姓名”。
不能用下式表示: πSNAME,AGE(σCNO≠’C2’(S⋈SC))
一定要用“差”的形式:
πSNAME,AGE(S)-πSNAME,AGE(σCNO=’C2’(S⋈SC))
(3)对于具有“全部”或“包含”问题的检索,一般要用除法操作表示
例: “检索学习全部课程的学生学号”:
πSNO,CNO(SC)÷πCNO(C)
不能表示为:πSNO (SC÷πCNO(C))