支持向量机（SVM），适合初学者读的一篇博客

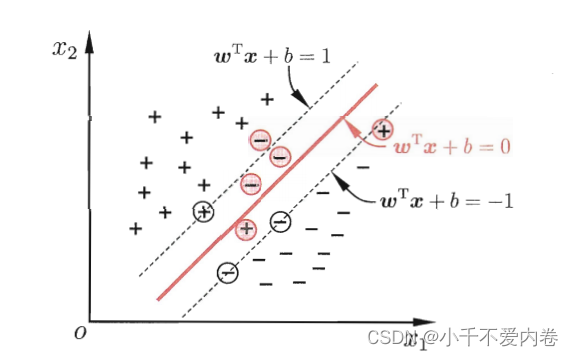
目标：找到一个超平面，将不同类别的样本分开。这样的超平面可能有很多，如下图，在这些超平面中，我们想要这个超平面有比较好的泛化能力，因此，应该选较粗的那个，这个有什么特点呢？该平面是“正中间”的那个！
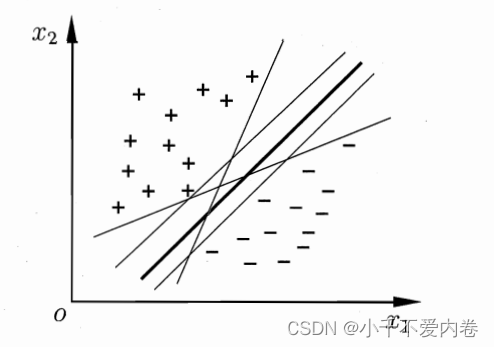
在这里插入图片描述

间隔和支持向量

划分的超平面用如下线性方程描述：
$w^Tx+b=0$
其中， $w=(w_1;w_2;…;w_d)$ 为法向量，决定了超平面的方向，b为位移项，决定了超平面和原点间的距离。
任意点x到超平面的距离为：
$r=\frac{|w^Tx+b|}{||w||}$
为了将样本正确分类，应该有 $(x_i, y_i)\in D$ 有，若 $y_i=1$ （正例），则有 $w^Tx_i+b>0$ ;若 $y_i=-1$ （反例），则有 $w^Tx_i+b<0$ 。为了提升泛化性能，我们想要将这种差距拉大，因此对上个式子进行了放缩（放缩是有前提的，数据需要能够r可分，就是存在r这么宽的一条线，使得数据被分开。在这里，r等于 $\frac{2}{||w||}$ ，因此不等式右边为1，当然遇到特殊问题，可以替换r），得到：
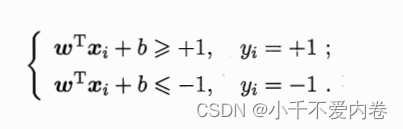
在这里插入图片描述
距离超平面最近的点，应该使得上式等号成立。这种距离最近的点成为“支持向量”。超平面应该位于正例的支持向量和负例的支持向量的正中间。此时，正例支持向量和负例的支持向量间的距离为：

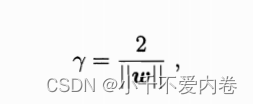
直观图如下。
一个问题：这个r越大越好？还是越小越好？答案是显然的，应该越大越好，越大说明两个类别的数据被分的越开。相反，如果这个距离很小，说明两类数据并没有分的特别开，泛化能力可想而知。
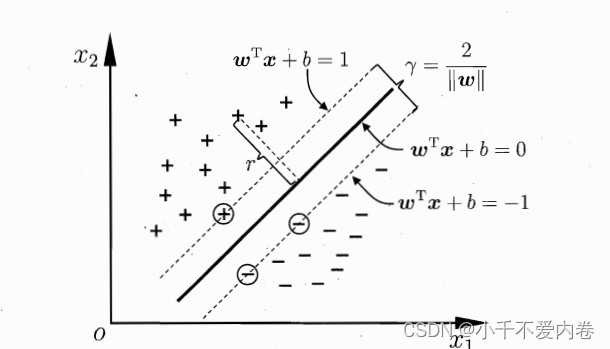
在这里插入图片描述
根据上面的思想，我们可以构造我们的优化函数了，就是在一定的条件下（正例和反例都分类正确的情况下），最大化距离r！

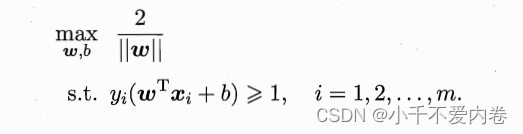
机器学习中，总是将最大化问题转化为最小化问题，上式就可以重写为：

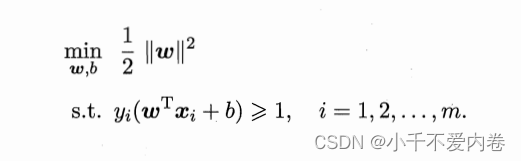
这就是支持向量机的基本型！下面该怎么解w和b呢？使用“对偶问题”进行求解！

对偶问题

（如果看不懂可以跳过，这部分是在通过一些数学方法算出w和b）
整个的求解思路是，使用拉格朗日乘子法，引入变量 $\alpha_i$ ，将w和b都转化为 $\alpha_i$ 的表达式，再通过求解 $\alpha_i$ ，进一步借出w和b。

拉格朗日乘子法表达式：

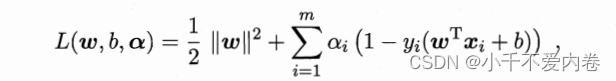
所以现在的优化函数变为了：
$min_{w,b}max_{\alpha_i}L(w,b,\alpha)$
由于需要从内到外计算，然而内部的 $max_{\alpha_i}L(w,b,\alpha)$ 并不容易求偏导，因此进行转换！转换为：
$max_{\alpha_i}min_{w,b}L(w,b,\alpha)$
这样就可以在内部对w和b求偏导了！得到：

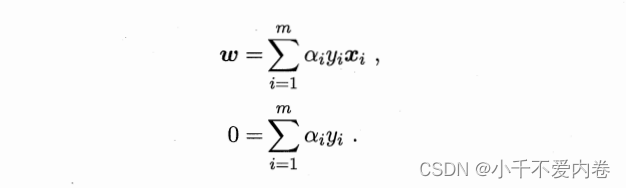
再将得到的式子带入到 $L (w, b, a)$ 中，得到对偶问题：

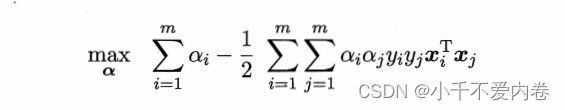
条件为：

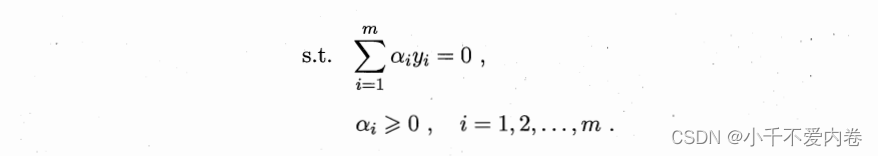
请观察这个式子，x，y我们都是知道的，将所有点和上面根据对b求偏导所得到的条件代入到这个式子中，就能够求得所有的 $\alpha_i$ 了。之后带入上面根据对w求偏导得到的式子，就能够求得w了。
说明，根据对偶问题求得的 $\alpha_i$ 需要满足一定的条件，即kkt条件：

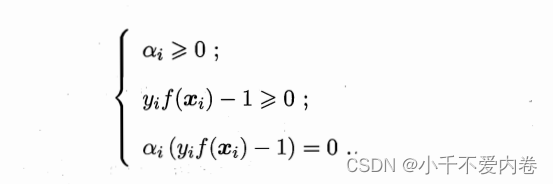
因此，如果借出的一些值不符合这个条件的，需要舍弃。解出的结果中有一些结果不为0，有一些结果是为0的，根据下面的式子可以看出，为0的对w的值并没有任何的影响，说明该点不是支持向量，不为0的才会对w起作用，说明该点是支持向量！超平面只和局部数据有关！

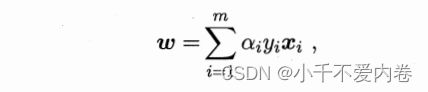
在这里插入图片描述
至于如何求b？对于支持向量，我们有 $y_sf(x_s)=1$ ，则有

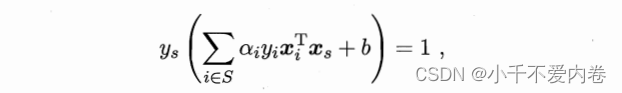
请观察这个式子， $y_s,\alpha_i,y_i,x_i,x_s$ 这些变量都是知道的，仅b不知道，因此可以轻松接出来b的值。
到此为止，我们得到了超平面的表达式！

核函数

前面的支持向量机对于线性可分的数据可以做到很好的分类，但是对于线性不可分的呢？如何做到分类？核心思想就是，假如说二维的数据线性不可分，那么我想办法把这些数据点映射到三维或者更高维，映射过后的数据点能够表示之前的数据点，在更高维的空间中这些数据点线性可分，并找到一个高维空间的超平面进行分类。如下图所示。
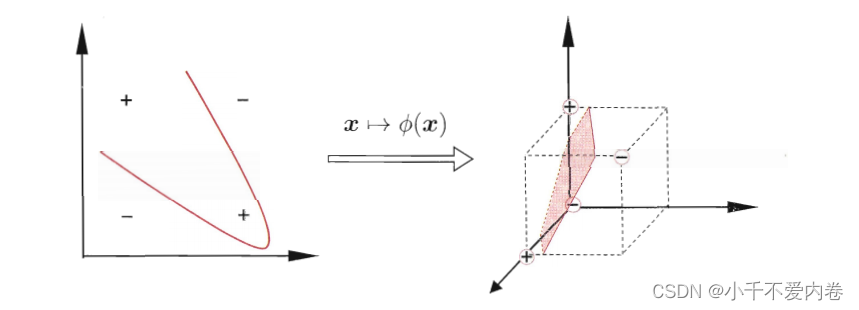
在这里插入图片描述
经过证明，如果原始空间是有限维，即属性数目有限，那么一定存在一个高维特征空间使得样本可分！
假设映射关系为 $x\to \phi(x)$
那么，类似于上一章，我们的优化函数就变成了：

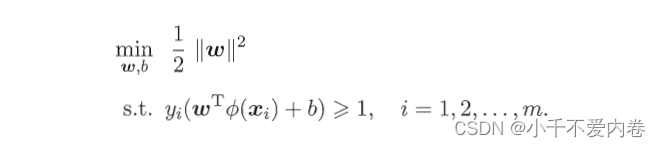
对偶问题是：

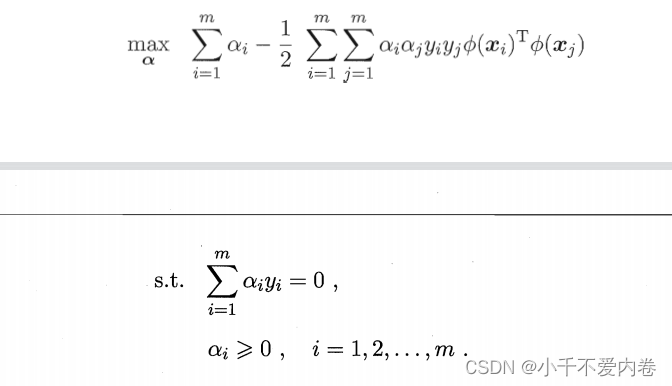
请注意这个式子，最右边有一个 $\phi(x_i)^T\phi(x_j)$ ，这是样本映射过后的内积，这个很难算的！为什么？因为映射过后的维度可能相当高！怎么避开这个问题？数学上可能找到这样一个函数，这个函数能将映射过后的内积转化为映射前数据之间的运算（映射前数据是有限维的，就能够方便地进行计算了），如下：
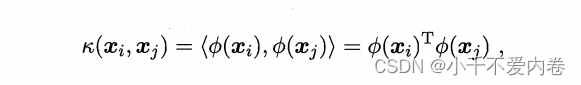
在这里插入图片描述

$\kappa(x_i,x_j)$ 就被称为核函数， $x_i,x_j$ 在高维空间的内积等于他们原始样本空间中通过核函数计算出来的结果。
ok，还是经过一系列相似的计算，求出超平面，超平面如下：
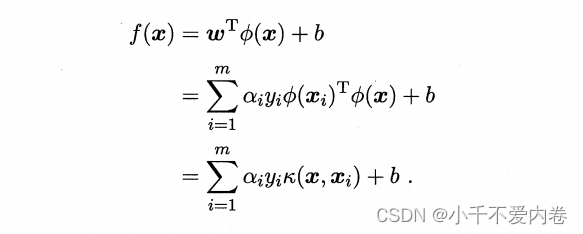
在这里插入图片描述
按说， $\phi(x)$ 应该是与核函数一一对应的，然而，现实中，能够满足以上条件的核函数并不多，一般有以下几个常用的核函数：

软间隔

前面的讨论中，我们默认超平面是能够将所有的数据全部分开的，现实生活中，往往有一些错误的数据点，而这些数据点如果被作为支持向量，则会对超平面产生很大的影响。我们能不能给予超平面一些宽松的条件，即不需要将所有的数据完全分开，这样有利于泛化性能的提升。为此引入“软间隔”，示意图如下：
在这里插入图片描述
为此，将之前的优化函数引入一个松弛变量：

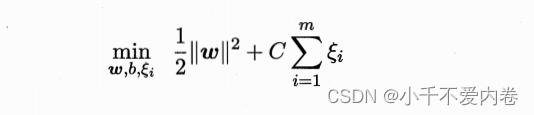
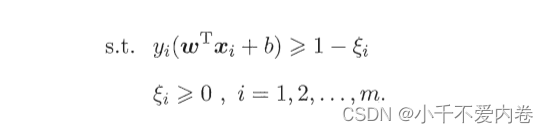
条件进行了一些宽松，即不需要完全大于等于1。这个松弛变量用以表征该样本不满足约束的程度。继续用之前的拉格朗日乘子法，对偶问题进行求解，就能够得到w和b了！

总结

思想与计算：支持向量机的思想是找到超平面将样本分开，这个超平面需要在两类数据的正中间，并且间隔越大越好！根据间隔越大越好就能够构造优化函数，进而使用拉格朗日乘子法进行求解。
核函数：对于无法线性可分的样本，我们想办法将这些样本映射到更高维的空间，使得可以线性可分，这就引入了映射函数，但是计算过程中很难算出映射后的内积，因此引入了核函数，将映射后的内积运算转化为了映射前的样本运算。而常用的核函数就那么几个！
软间隔：最后，为了防止一些错误数据的干扰，提升泛化性能。引入了软间隔，使得超平面的约束条件不那么严格！松弛变量表征了不满足约束的程度。