学习数学建模原理与应用【插值与拟合基本原理与编程实现】

主要内容

插值与拟合是数学建模中的一种基本的数据分析手段被公认为建模中的常用算法之一
学习了插值问题、插值原理、高次插值的Runge现象，Matlab中的一维和二维插值命令
拟合问题、拟合原理与步骤,然后介绍了Matlab的拟合计算。

插值

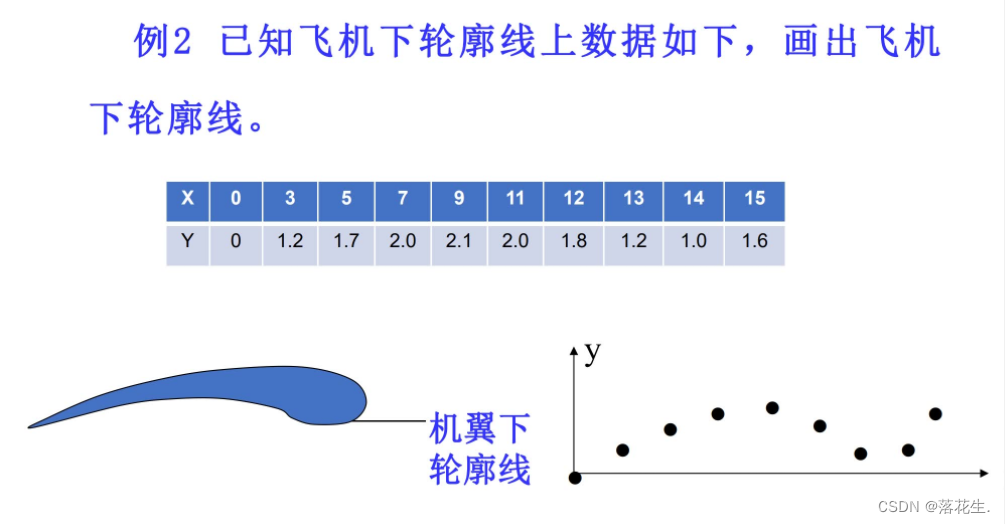
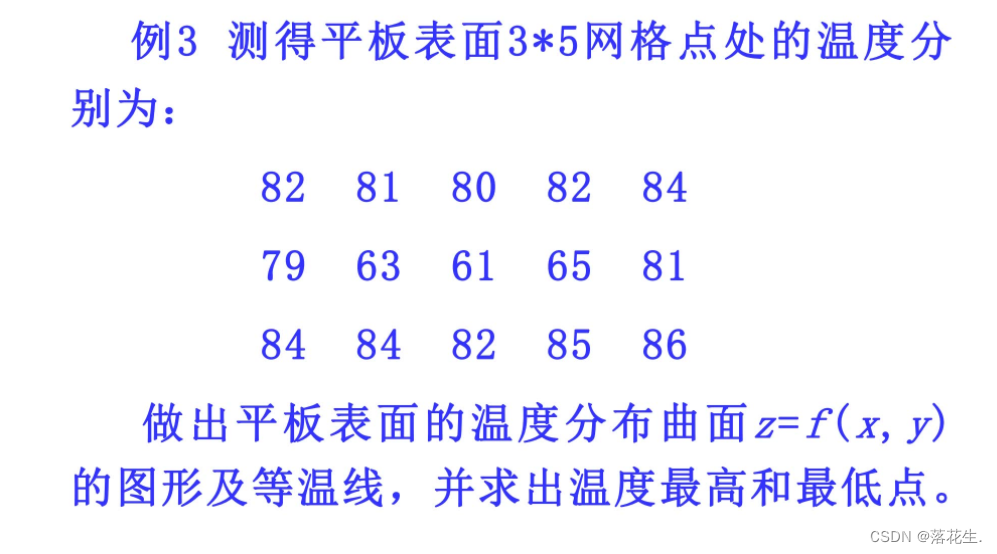
上述问题可归结为“已知函数在某区间(域)内若干点处的值，求函数在该区间(域)内其它点处的值”，这种问题适宜用插值方法解决。
一维插值问题可描述为: 已知函数在Xo, x1,···,xn处的值Yo, Y1,···, Yn，求简单函数p(x)，使 p(xi) = yi通常取p(x)为多项式
可以用范德蒙行列式和克莱姆法则证明:
在x0，x1,xn处取值y0，y1，·yn的多项式存在且唯一，即插值问题的解唯一存在。
常用的插值方法有Lagrange插值法和Newton插值法。

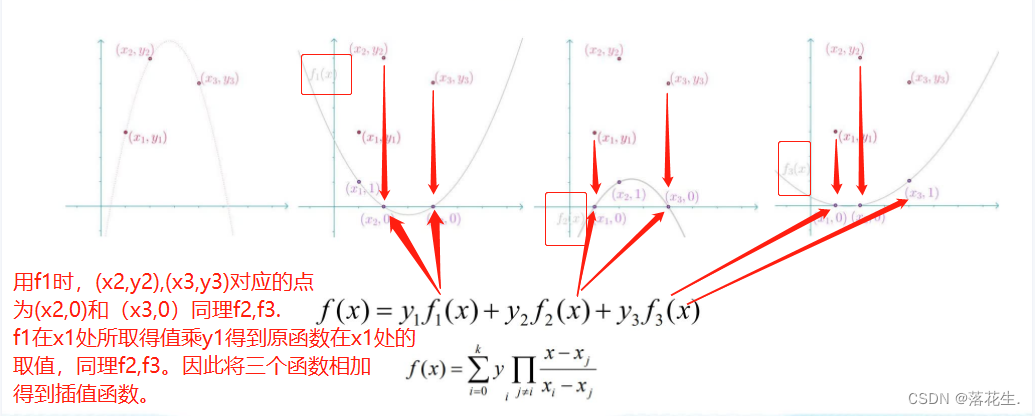
拉格朗日插值法

拉格朗日插值公式(外文名Lagrange interpolation formula指的是在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值的一种插值多项式。

高次插值的Runge现象（龙格现象）

插值多项式的次数越高，插值精度越高。结论仅仅在插值多项式的次数不超过七时成立;插值多项式的次数超过七时，插值多项式会出现严重的振荡现象，称之为Runge现象。

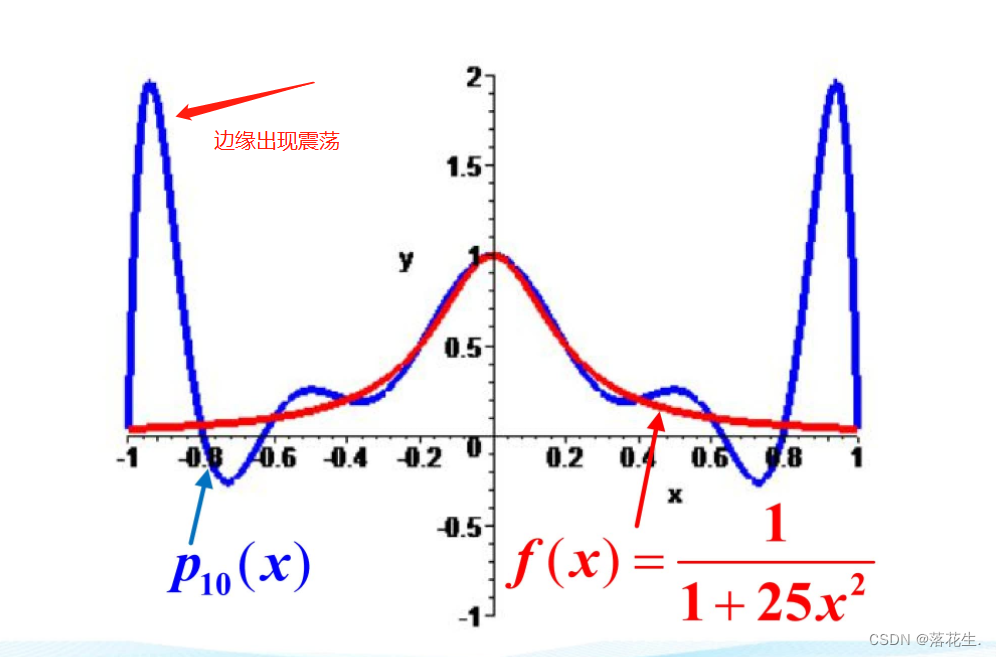
在实际中不应使用七次以上的插值。
避免Runge现象的常用方法是: 将插值区间分成若干小区间，在小区间内用低次(二次，三次)插值，即分段低次插值，如样条函数插值。

MATLAB插值

1.一维插值

一维插值命令是interp1，其基本格式为yi= interp1(x,y,xi, ‘method’).
x,y为已知点，xi,yi为被插值点和插值结果，x,y和xi,yi通常为向量;
method’表示插值方法:
nearest’-最邻近插值
‘linear’-线性插值
spline’-三次样条插值，
'cubic’一立方插值，
缺省为线性插值。

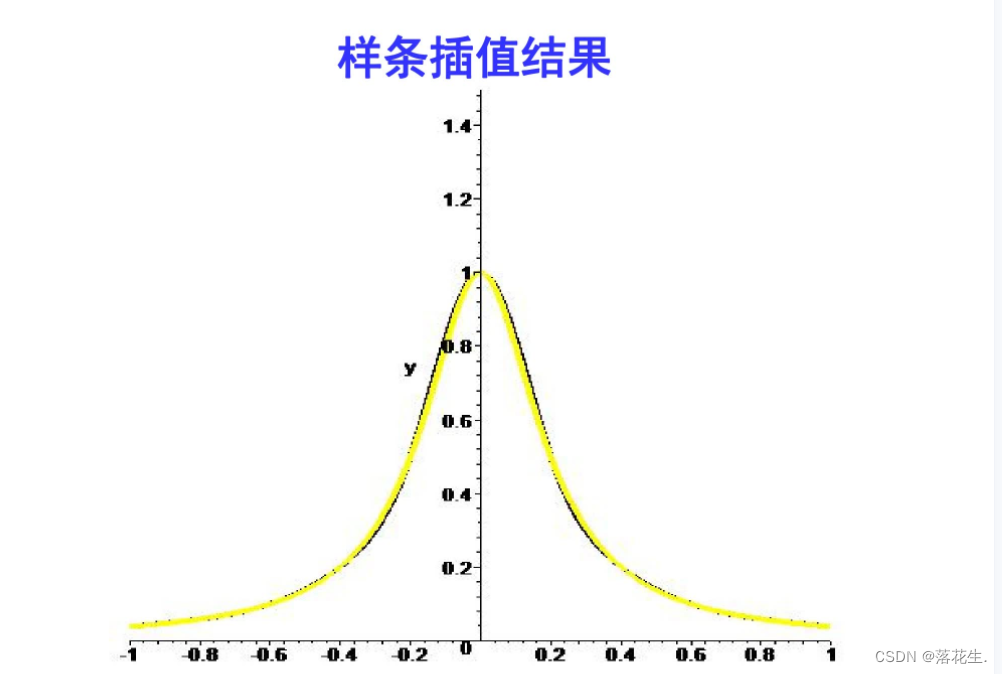
三次样条插值编程应用

x=0:2:24;
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
x1=13;%插值点在13处
yl=interp1(x,y,x1,'spline')%求出在该点的值
xi=0:1/3600:24;
yi=interp1(x,y,xi, 'spline');
plot(x,y,'*',xi,yi)

在x=13处的值

所画出的图

三种插值法的比较

首先创建拉格朗日插值函数并命名为lagrange.m文件
函数代码如下

function y=lagrange(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:m
    z=x(i);
    s=0.0;
    for k=1:n
        p=1.0;
        for j=1:n
            if j~=k
                p=p*(z-x0(j))/(x0(k)-x0(j));
            end
         end
s=p*y0(k)+s;
    end
     y(i)=s;
en

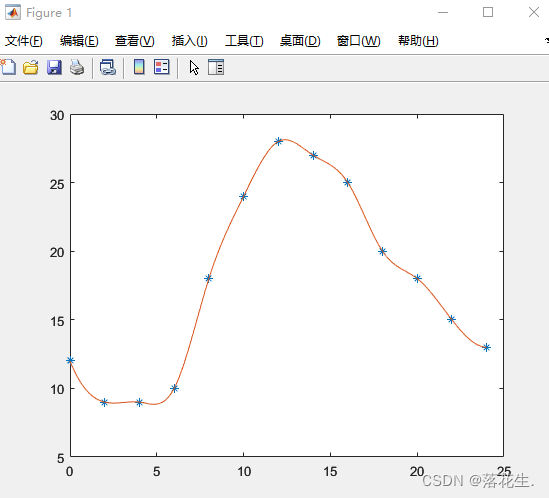
创建程序%拉格朗日插值，线性插值法和三次样条插值的比较

x0=[0 3 5 7 9 11 12 13 14 15 ];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y1=lagrange(x0,y0,x);%使用拉格朗日插值法
y2=interp1(x0,y0,x);%使用一维插值命令的线性插值法
y3=interp1(x0,y0,x,'spline');%使用一维插值命令的三次样条插值法
subplot(3,1,1);
plot(x0,y0,'k+',x,y1,'r');
grid;%生成网格点
title('lagrange');
subplot(3,1,2);
plot(x0,y0,'k+',x,y2,'r');
grid;
title('piecewise linear');
subplot(3,1,3);
plot(x0,y0,'k+',x,y3,'r');
grid;
title('spline');

运行结果

结果表明此处用三次样条插值法更好一些

• 程序依次用Lagrange、分段线性和三次样条三种插值方法进行了计算其中Lagrange高次插值明显出现了Runge现象;
• 因为Matlab没有Lagrange高次插值功能，所以程序中单独编写了高次插值函数lagrange，然后调用。

2.二维插值

二维插值命令是interp2，基本格式为zi=interp2(x,y,z,xi,yi,‘method’).二维插值命令的使用较复杂
x,y,z为已知插值点，z可以理解为被插值函数在(x,y)处的值;xi,yi为被插值点,zi为输出的插值结果，可理解为插值函数在(xi,yi)处的值;x,y为向量，xi,yi为向量或矩阵而z和zi则为矩阵。
'method’表示插值方法:
'nearest’一最邻近插值，
‘linear’-双线性插值
‘spline’-双三次样条插值，
'cubic’双立方插值，
默认双线性插值。
程序实践

x=1:5;
y=1:3;%表示三行五列的数据，x在此表示列数，y在次表示行数
temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
figure(1);
mesh(x,y,temps);
xi=1:0.2:5;
yi=1:0.2:3;
zi=interp2(x,y,temps,xi,yi','cubic');
figure(2);
mesh(xi,yi,zi);
figure(3);
contour(xi,yi,zi,20,'r');%画出20条等高线
[i,j]=find(zi==min(min(zi)));
%==表示判断或者寻找位置，
% min(zi)寻找每一列最小值，min(min(zi))在得到的最小值中继续寻找最小值
x=xi(j),y=yi(i),zmin=zi(i,j)
[i,j]=find(zi==max(max(zi)));
x=xi(j),y=yi(i),zmax=zi(i,j)

运行结果




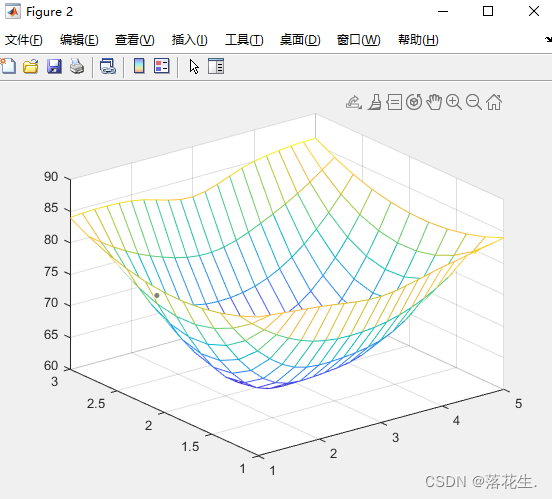
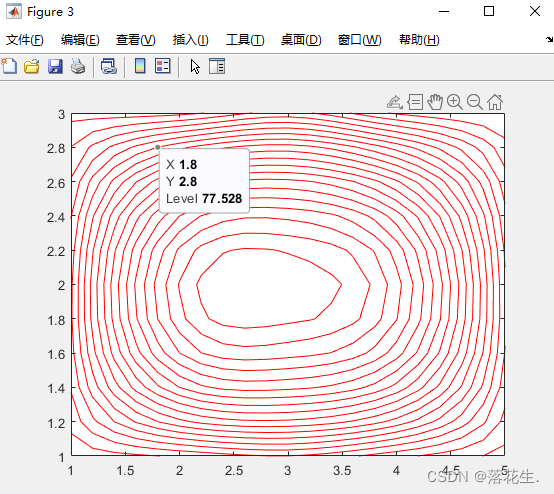
(1) interp2中的xi为行向量，而yi为列向量，其实xi和yi行列不同即可。
(2) plot3(空间曲线),
mesh(空间曲面)
surf (空间曲面)，
contour(等高线)是三维作图中的常用命令。
mesh和surf的区别是mesh画的是曲面网格图，只是单纯的用网格连接起来。而surf画的是曲面表面图。
contour(x,y,z,n)的功能是作出由点(x,y,z)插值而成曲面的n条等高线。
用meshc和surfc可在曲面下方画等高线
meshz和surfz是画垂帘图
如果除去figure,则只会画出最后一个图象，作用有点类似于hold on


程序

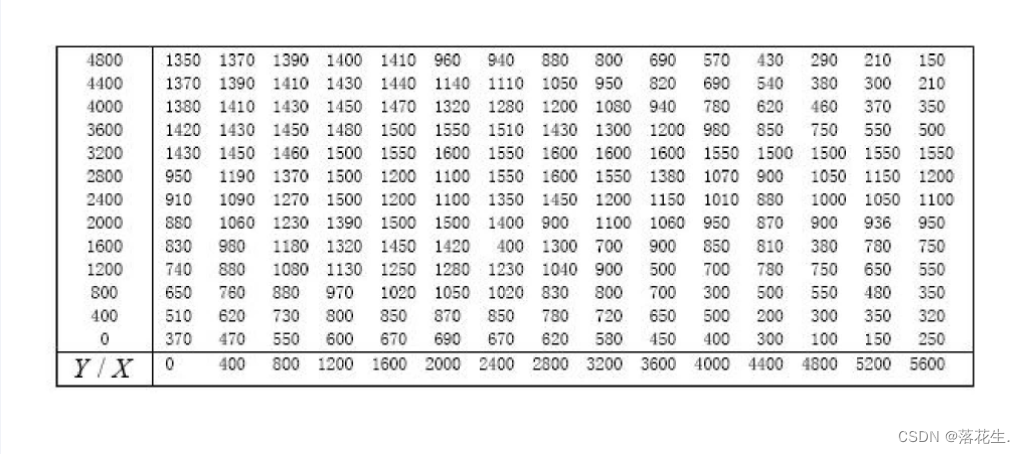
x=0:400:5600;
y=0:400:4800;
z=[370 470 550 600 670 690 670 620 580 450 400 300 100 150 250;...
    510 620 730 800 850 870 850 780 720 650 500 200 300 350 320;...
    650 760 880 970 1020 1050 1020 830 900 700 300 500 550 480 350;...
    740 880 1080 1130 1250 1280 1230 1040 900 500 700 780 750 650 550;...
    830 980 1180 1320 1450 1420 1400 1300 700 900 850 840 380 780 750;...
    880 1060 1230 1390 1500 1500 1400 900 1100 1060 950 870 900 930 950;...
    910 1090 1270 1500 1200 1100 1350 1450 1200 1150 1010 880 1000 1050 1100;...
    950 1190 1370 1500 1200 1100 1550 1600 1550 1380 1070 900 1050 1150 1200;...
    1430 1430 1460 1500 1550 1600 1550 1600 1600 1600 1550 1500 1500 1550 1550;...
    1420 1430 1450 1480 1500 1550 1510 1430 1300 1200 980 850 750 550 500;...
    1380 1410 1430 1450 1470 1320 1280 1200 1080 940 780 620 460 370 350;...
    1370 1390 1410 1430 1440 1140 1110 1050 950 820 690 540 380 300 210;...
    1350 1370 1390 1400 1410 960 940 880 800 690 570 430 290 210 1501];
figure(1);
meshz(x,y,z);%带帷幕的网格曲面图
xlabel('X'),ylabel('Y'),zlabel('Z');
[xi,yi]=meshgrid(0:50:5600,0:50:4800);%基于向量 x 和 y 中包含的坐标返回二维网格坐标
figure(2);
z1i=interp2(x,y,z,xi,yi,'nearest');%最邻近插值法
surfc(xi,yi,z1i);%画垂帘图
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(3);
z2i=interp2(x,y,z,xi,yi);%默认双线性插值法
surfc(xi,yi,z2i);
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(4);
z3i=interp2(x,y,z,xi,yi,'cubic');%双立方插值法
surfc(xi,yi,z3i);
xlabel('X'),ylabel('Y'),zlabel('Z');
figure(5);
subplot(1,3,1),contour(xi,yi,z1i,10,'r');
subplot(1,3,2),contour(xi,yi,z2i,10,'r');
subplot(1,3,3),contour(xi,yi,z3i,10,'r');%画出三个图的等高线

程序用“[xi,yi]=meshgrid(0:50:5600,0:50:4800);”生成网格点(xi,yi)，作用相当于“xi=0:50:5600;yi=0:50:4800;”但meshgrid(x,y)生成的xi,yi为同维矩阵xi的行均为x，而yi的列均为y。
运行结果

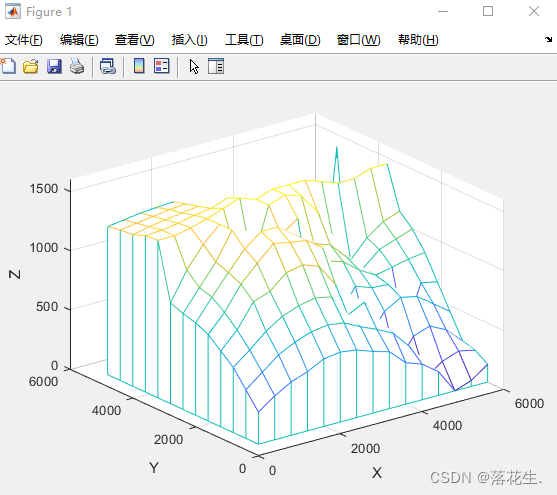
最邻近点插值

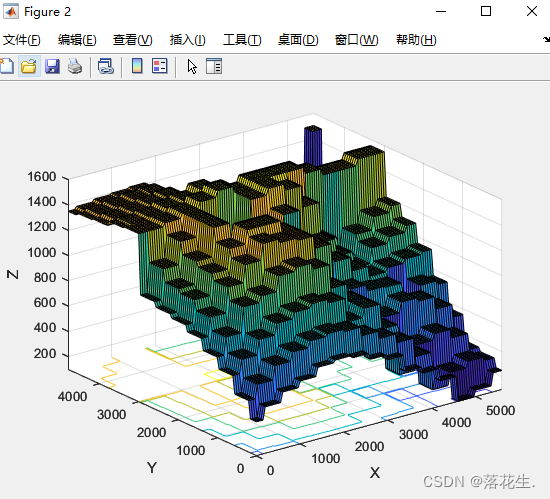
双线性插值

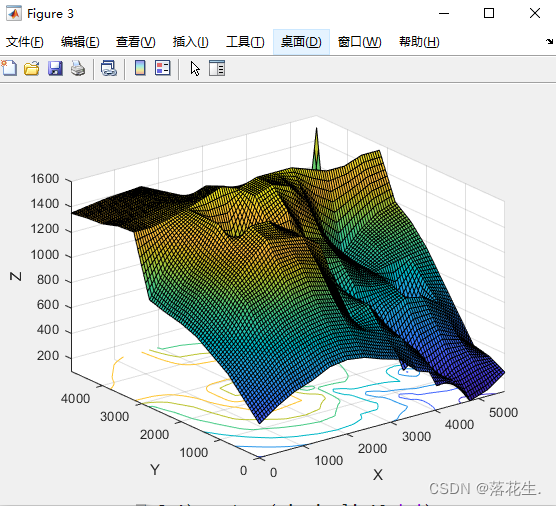
双三次插值

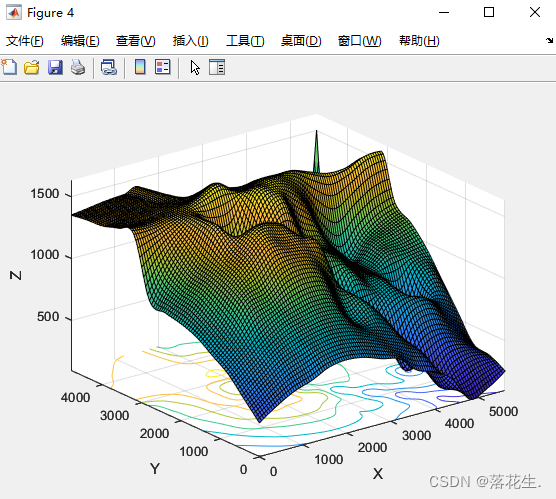
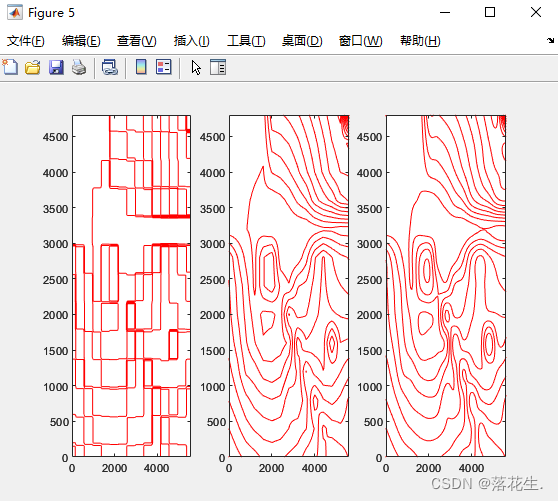
散乱点插值

前面讨论的插值问题的插值点(x,y)均为网格点。当(x,y)为散乱点时，可用griddata(x,y,z,xi,yi,‘method’) 命令进行二维插值。

示例

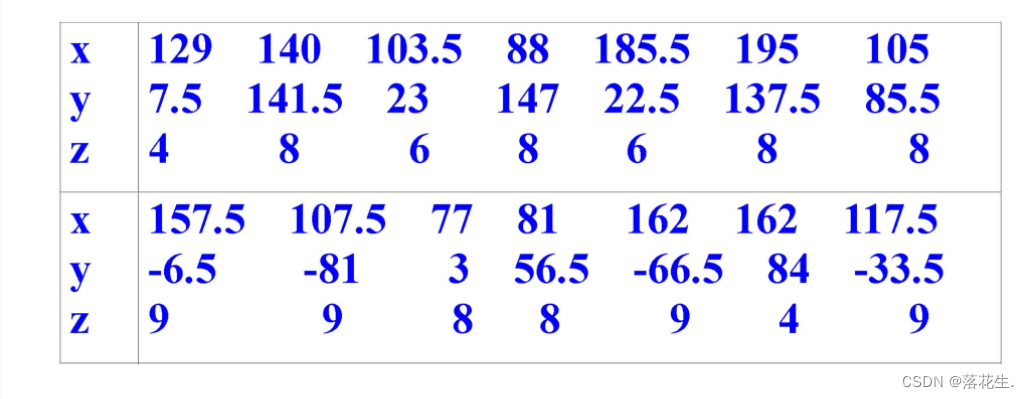
程序

x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];
[xi,yi]=meshgrid(75:0.5:200,-70:0.5:150);%基于向量 x 和 y 中包含的坐标返回二维网格坐标
zi=griddata(x,y,z,xi,yi,'cubic');%对二维或三维散点数据插值,双立方插值法
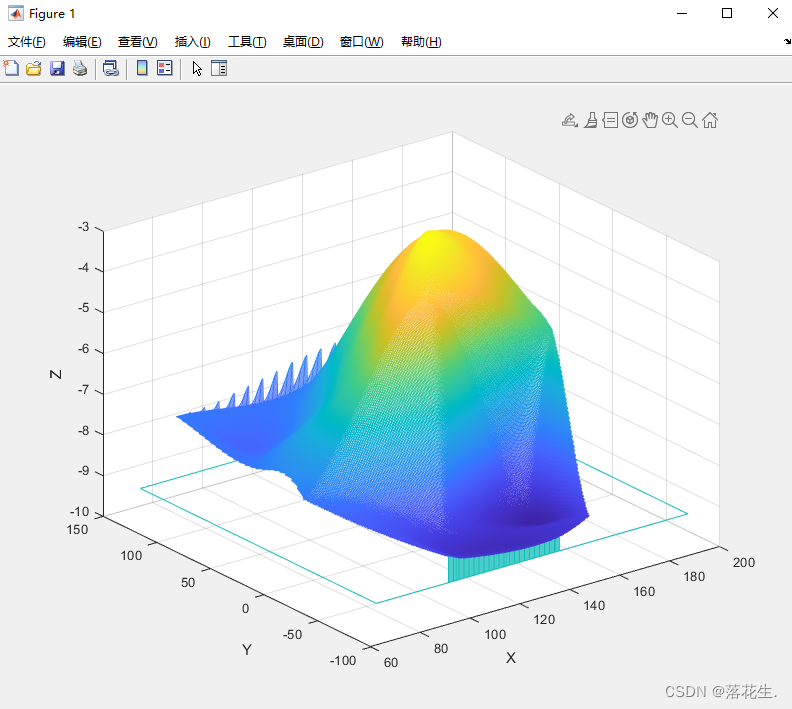
figure(1);
meshz(xi,yi,zi);%带帷幕的网格曲面图
xlabel('X'),ylabel('Y'),zlabel('Z');
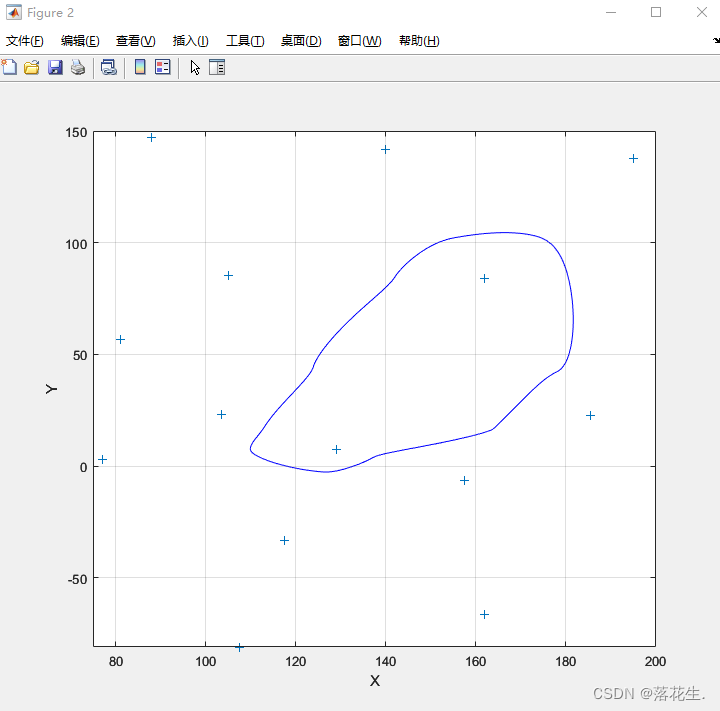
figure(2);
contour(xi,yi,zi,[-5 -5], 'b');%画出高度-5的等高线
grid;%显示或隐藏坐标区网格线
hold on;
plot(x,y,'+');
xlabel('X'),ylabel('Y');

运行结果

拟合问题

例子

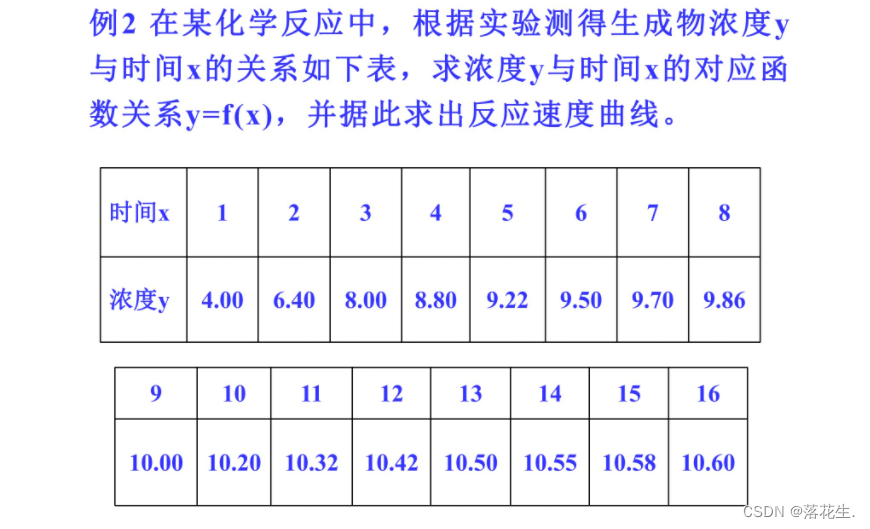
例1的第1问是典型的插值问题，但第2问不宜用插值方法，因为13.5已超出所给数据范围用插值函数外推插值区间外的数据会产生较大误差
用Matlab求出的高次插值、样条插值及外推的结果

高次插值出现了Runge现象，外推t>12时的数据出现了巨大误差。
样条插值的第一个图表明样条插值可以很好地解决第一个问题，但第二个图显示，用样条插值外推t>12时的数据也会产生较大误差。
综上，第二问不宜用插值方法。
解决第2问的常用方法是，根据1到12点间的温度数据求出温度与时间之间的近似函数关系f(t)，由f(t)推断t =13.5时的温度这种根据离散数据求数据间近似函数关系的问题称为曲线拟合问题
拟合问题与插值问题的区别在于:
(1) 插值函数过已知点，而拟合函数不一定过已知点;
(2) 插值主要用于求函数值，而拟合的主要目的是求函数关系，从而进行预测等进一步的分析。
当然，某些特定问题既可以用插值也可以用拟合。
例二也是拟合问题

2.拟合的计算

(1) 线型的选择:
(2) 线型中参数的计算。线型的选择是拟合计算的关键和难点通常主要根据专业知识和散点图确定线型。线性拟合中参数的计算可采用最小二乘法，而非线性拟合参数的计算则要应用Gauss-Newton迭代法。

3.Matlab拟合

Matlab多项式拟合命令格式为:
[a,S]=polyfit(x,y,n)其中，x和y是被拟合数据的自变量和因变量; n为拟合多项式的次数; a为拟合多项式系数构成的向量; S为分析拟合效果所需的指标(可省略)
代码展示拟合一组数据

%拟合
x=1:12;
y=[5, 8, 9, 15,25, 29, 31, 30, 22, 25, 27, 24];
a=polyfit(x,y,9);%进行9次多项式拟合
xp=1:0.1:12;
yp=polyval(a,xp);%计算多项式 a 在 xp 的每个点处的值。
% 参数 a 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）
plot(x,y,'.k',xp,yp,'r');

结果如下

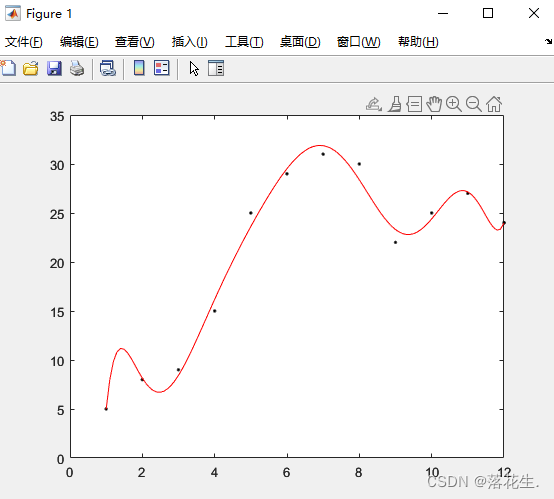
(2）非线性拟合
Matlab非线性拟合命令格式为:[b,r]=polyfit(x,y,fun,b0,option)
其中，x和y是被拟合数据的自变量和因变量; fun为拟合函数; b0为拟合参数的初始迭代值; option为拟合选项;b为拟合参数;r为拟合残差。
利用例二进行MATLAB实践

x=1:16;
y=[4.00 6.40 8.00 8.80 9.22 9.50 9.70 9.86 10.00 10.20 10.32 10.42 10.50 10.55 10.58 10.60];
y1=@(b,t)b(1)*exp(-t/b(2))+b(3)*exp(-t/b(4))+b(5);%此关系式可以写的更简单一些，作用只是确定拟合函数的类型
b0=[-1 1 -1 1 1];%初值
a=nlinfit(x,y,y1,b0);%nlinfit非线性回归拟合，此处等效polyfit。
xp=1:0.1:16;
yp=y1(a,xp);%带插点的坐标
plot(x,y,'.k',xp,yp,'r');

用MIatlab编程进行拟合有诸多的不方便
(1) 需要编程。比如在例2的程序中要用到匿名函数，这对初学者而言并不容易。
(2) 拟合结果不完整。Matlab拟合命令般只提供拟合系数等基本结果。若要获取表示拟合优劣的统计量有时需要另外计算。
(3) 不能保证非线性拟合迭代收敛。由于非线性拟合的初始迭代参数需要人为取定，所以不能保证迭代一定收敛。
所以可以借助MATLAB工具箱cftool(曲线拟合器)

cftool(曲线拟合器)

对例二的数据利用cftool工具箱进行拟合


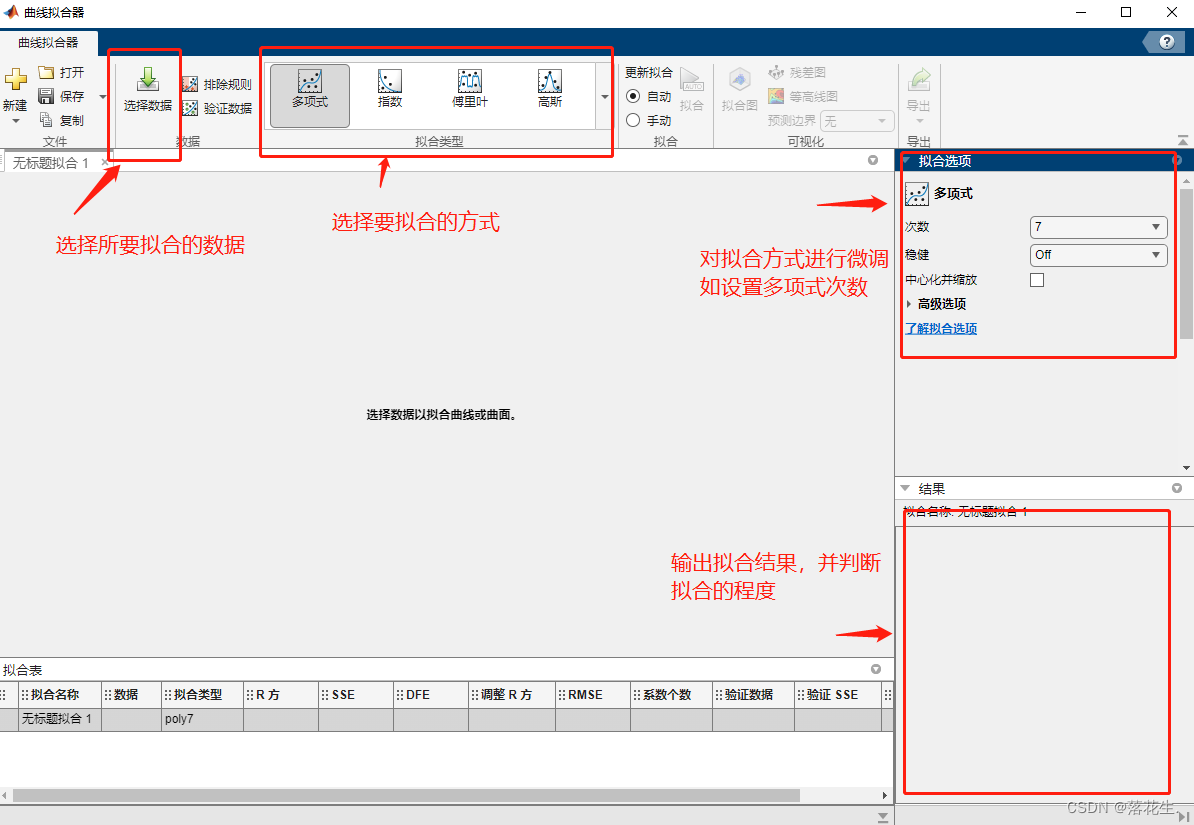
在七次多项式拟合下的输出

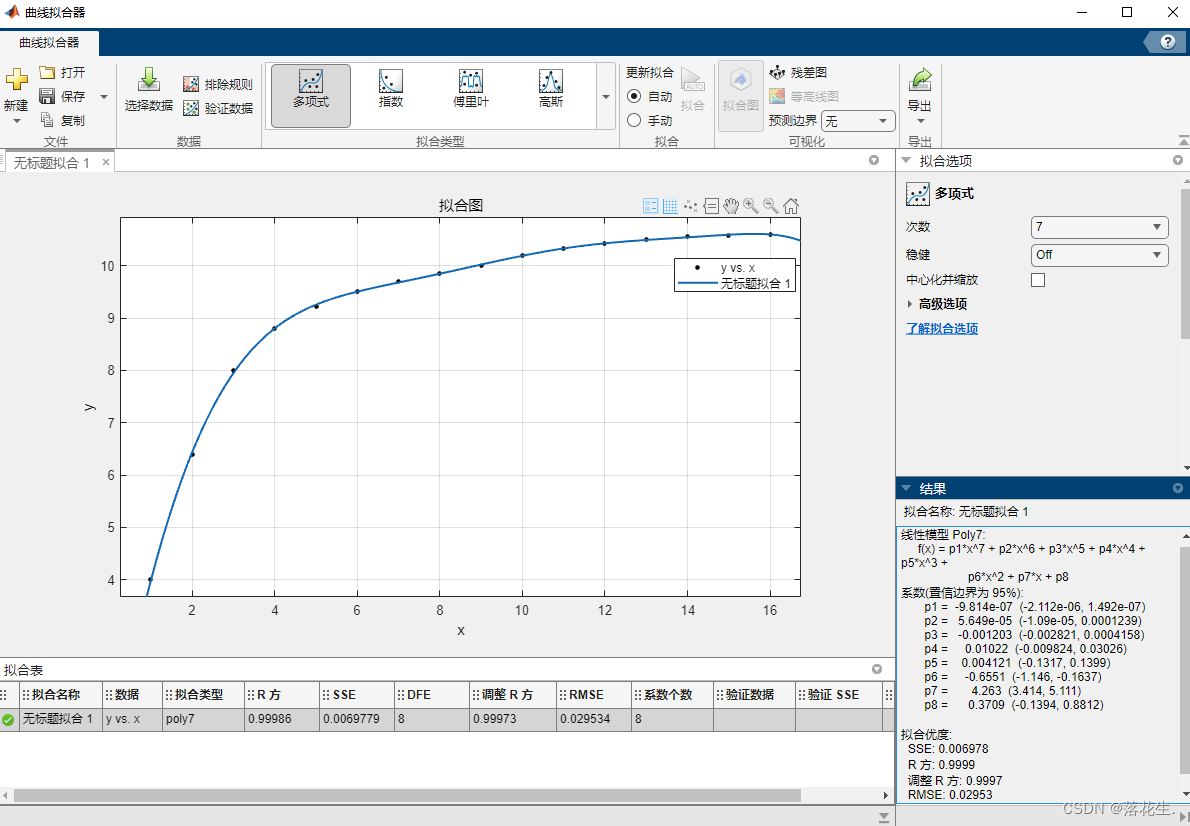
拟合完成以后会对拟合的结果进行评价
SSE-均方根误差/剩余平方和误差
R 方-相关系数
RMSE-剩余标准差
一般看SSE和RMSE,不超过0.1即可。
选择右上角的导出可以导出代码。
这个工具箱很好用。