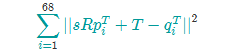Procrustes analysis

概述

在人脸相关应用中，获得的人脸图像常常形状各异，这时就需要对人脸形状进行归一化处理。人脸对齐就是将两个不同的形状进行归一化的过程，将一个形状尽可能地贴近另一个形状。

值得注意的是，在英语文献中，Face Alignment和Facial Landmark Detection常常混用，在我的系列博客里面，Facial Landmark Detection指的是人脸特征点检测，而Face Alignment指的是人脸对齐。人脸特征点检测是人脸对齐的必要步骤，现在有很多端到端(end to end)的方法不需要进行对齐，所以具体要不要对齐这一步需要结合实际分析。

人脸特征点检测的结果如下:

landmark

人脸对齐的效果如下，可以看到右边的脸已经和左边的脸形状大体一致：

face align

言归正传，Procrustes analysis是一种用来分析形状分布的统计方法。Procrustes源于古希腊神话中的一个强盗，他常切断受害者的肢体使其身形与床相匹配，类似地Procrustes分析方法是对两个形状进行归一化处理。从数学上来讲，普氏分析就是利用最小二乘法寻找形状A到形状B的仿射变换。

模型

仿射变换

在高中的几何课程中，一定学过平移，放缩和旋转变换。

仿射变换

将这三种变换写成矩阵形式：

这个式子中，s就是缩放比例，就是旋转角度，最后的t代表平移的位移，其中R是一个正交矩阵。

我们现在要解决如何旋转、平移和缩放第一个向量，使它们尽可能对齐第二个向量的点。一个想法是使用仿射变换将第一个图像变换覆盖第二个图像。如何判断这种对齐的效果呢？使用最小二乘法，使得变化后所有点与目标点距离和最小。

两个形状矩阵分别为p和q，矩阵的每一行代表一个特征点的x,y坐标，假设有68个特征点坐标，则。写成数学形式：

其中就是p矩阵的第i行。写成矩阵形式：

代表Frobenius范数，就是每一项的平方和。

求解

这个最小值问题是有解析解的。

先放上代码：

#Procrustes analysis
def transformation_from_points(points1, points2):
    points1 = points1.astype(numpy.float64)
    points2 = points2.astype(numpy.float64)

    c1 = numpy.mean(points1, axis=0)
    c2 = numpy.mean(points2, axis=0)
    points1 -= c1
    points2 -= c2

    s1 = numpy.std(points1)
    s2 = numpy.std(points2)
    points1 /= s1
    points2 /= s2

    U, S, Vt = numpy.linalg.svd(points1.T * points2)
    R = (U * Vt).T

    return numpy.vstack([numpy.hstack(((s2 / s1) * R,
                                       c2.T - (s2 / s1) * R * c1.T)),
                         numpy.matrix([0., 0., 1.])])

根据

https://en.wikipedia.org/wiki/Orthogonal_Procrustes_problem

可以知道

是有解的。

需要将式子

进行一些变化，写成Wikipedia式子的形状。这里的变化就需要对原始点集p和q进行一些处理，使得最小化式子发生变化。

https://en.wikipedia.org/wiki/Procrustes_analysis#Ordinary_Procrustes_analysis

这里给出了对原始点集的变化步骤。结合代码来看：

    c1 = numpy.mean(points1, axis=0)
    c2 = numpy.mean(points2, axis=0)
    points1 -= c1
    points2 -= c2

这一步处理消除了平移T的影响。

    s1 = numpy.std(points1)
    s2 = numpy.std(points2)
    points1 /= s1
    points2 /= s2

这一步处理消除了缩放系数s的影响。

这两步处理以后，R就可以变成求解下面的式子：

这里的A，B不再是原始的数据点集，而是变成了处理以后点集。

根据维基百科，这个式子是可以求解的：

这样就解出了R：

    U, S, Vt = numpy.linalg.svd(points1.T * points2)
    R = (U * Vt).T

源代码最后一步返回的是仿射变换矩阵

用普氏分析(Procrustes analysis)调整脸部

现在我们已经有了两个标记矩阵，每行有一组坐标对应一个特定的面部特征（如第30行给出的鼻子的坐标）。我们现在要搞清楚如何旋转、翻译和规模化第一个向量，使它们尽可能适合第二个向量的点。想法是，可以用相同的变换在第一个图像上覆盖第二个图像。

把它们更数学化，寻找T，s和R，令下面这个表达式的结果最小：

图片描述

R是个2 x2正交矩阵，s是标量，T是二维向量，pi和qi是上面标记矩阵的行。

事实证明，这类问题可以用“常规普氏分析法” (Ordinary Procrustes Analysis) 解决：

def transformation_from_points(points1, points2):
    points1 = points1.astype(numpy.float64)
    points2 = points2.astype(numpy.float64)

    c1 = numpy.mean(points1, axis=0)
    c2 = numpy.mean(points2, axis=0)
    points1 -= c1
    points2 -= c2

    s1 = numpy.std(points1)
    s2 = numpy.std(points2)
    points1 /= s1
    points2 /= s2

    U, S, Vt = numpy.linalg.svd(points1.T * points2)
    R = (U * Vt).T

    return numpy.vstack([numpy.hstack(((s2 / s1) * R,
                                       c2.T - (s2 / s1) * R * c1.T)),
                         numpy.matrix([0., 0., 1.])])

代码分别实现了下面几步：

将输入矩阵转换为浮点数。这是之后步骤的必要条件。
每一个点集减去它的矩心。一旦为这两个新的点集找到了一个最佳的缩放和旋转方法，这两个矩心c1和c2就可以用来找到完整的解决方案。
同样，每一个点集除以它的标准偏差。这消除了问题的组件缩放偏差。
使用Singular Value Decomposition计算旋转部分。可以在维基百科上看到关于解决正交普氏问题的细节（https://en.wikipedia.org/wiki/Orthogonal_Procrustes_problem）。
利用仿射变换矩阵（https://en.wikipedia.org/wiki/Transformation_matrix#Affine_transformations）返回完整的转化。

之后，结果可以插入OpenCV的cv2.warpAffine函数，将图像二映射到图像一：

def warp_im(im, M, dshape):
    output_im = numpy.zeros(dshape, dtype=im.dtype)
    cv2.warpAffine(im,
                   M[:2],
                   (dshape[1], dshape[0]),
                   dst=output_im,
                   borderMode=cv2.BORDER_TRANSPARENT,
                   flags=cv2.WARP_INVERSE_MAP)
    return output_im