论文阅读之Robot Learning System Based on Adaptive Neural Control and Dynamic Movement Primitives

论文阅读其实就是用自己的话讲一遍，然后理解其中的方法

0、论文基本信息

为什么阅读这篇论文：因为它获得了IEEE TNNLS 2022年度最佳论文奖，年度唯一最佳论文奖(Outstanding Paper Award)，TNNLS目前的影响因子为10.4（截至到2023年9月），是中科院分区1区的Top期刊。
论文题目：Robot Learning System Based on Adaptive Neural Control and Dynamic Movement Primitives
期刊名称：IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS
论文作者：Chenguang Yang, Chuize Chen, Wei He, Rongxin Cui and Zhijun Li
发表年份：2019

作者简介：杨辰光教授是英国布里斯托机器人实验室主任，也是华南理工大学的教授，非常厉害的一位老师，机器人方向的大牛，Google学术被引超多，发表了多篇机器人方向的顶刊论文，包括TRO等，主要研究兴趣为神经网络和机器人控制（我还买了杨辰光老师联合编写的智能控制书籍，主要负责神经网络章节）。感觉杨辰光老师和贺威老师还有李智军老师都互相认识，他们联合发表了很多机器人方向的高质量论文，非常值得阅读。

题目：基于自适应神经控制和动态运动基元的机器人学习系统

摘要：本文提出了一种同时考虑 运动生成和轨迹跟踪的增强型机器人技能学习系统。在机器人学习演示过程中，使用动态运动基元（DMP）对机器人运动进行建模。每个DMP由一组动态系统组成，这些系统增强了生成目标运动的稳定性。此外，结合高斯混合模型和高斯混合回归，以提高DMP的学习性能，从而可以从多次演示中提取更多的技能特征。从学习到的模型生成的运动可以在空间和时间上缩放。此外，还为机器人设计了一个基于神经网络的控制器来跟踪运动模型产生的轨迹。在该控制器中，使用径向基函数神经网络来补偿动态环境造成的影响。使用Baxter机器人进行了实验，结果证实了所提出方法的有效性。

一、引言

运动生成
近年来，机器人在各个领域得到了广泛的应用，尤其是在制造业。由于制造产品的更新速度越来越快，因此需要适应性强的机器人。因此，有必要开发增强性机器人学习的方法。机器人示教学习（Learning from demonstration, LfD）是简化机器人学习策略的一种有价值的技术。人类导师展示了完成任务的方法，然后机器人通过运动建模来学习和再现技能。因此，必须考虑如何对运动进行有效建模。

动态系统（DS）是运动建模的强大工具。与传统方法（例如插值技术）相比，DS提供了一种灵活的解决方案来建模稳定和可扩展的轨迹。此外，用DS编码的运动对扰动是鲁棒的。一种基于DS的方法被用于学习人类运动，其中DS的未知映射使用称为极限学习机的神经网络（NN）进行近似[5]。所学习的模型显示出足够的稳定性和泛化能力。然而，这种基于DS的方法需要大量的演示数据来进行训练。相比之下，基于非线性DS的动态运动基元（DMP）只需要一次演示即可对运动进行建模；DMP将运动轨迹建模为与待学习的未知函数组合的弹簧-阻尼器系统。弹簧-阻尼器系统的固有特性增强了所产生运动的稳定性和鲁棒性（对扰动）。

本文主要考虑的的是将多个演示集成到一个DMP模型中。

概率方法在运动编码中显示出良好的性能，可以提取演示的固有可变性，从而可以保留演示的更多特征。诸多文献都利用了DS的鲁棒性和泛化能力，以及概率方法优异的学习性能。

为了利用DS和概率方法的性能，作者将DMP和GMM集成到提出的系统中，其中DMP的非线性函数用GMM建模，并通过GMR检索其估计。这种修改使机器人能够从多次演示中提取更多的运动特征，并生成合成这些特征的运动。使用局部加权回归（LWR）学习原始DMP，并使用局部加权投影回归优化LWR的每个内核的带宽。尽管学习过程增加了复杂性，但这些方法使DMP只能从一个演示中学习。储层计算（Reservoir computing）是另一种用于近似非线性函数的方法，但其计算效率低于GMR。

轨迹跟踪

机器人的模仿性能还取决于涉及机器人动力学的轨迹跟踪控制器的准确性。通常，如果模型足够准确，则基于模型的控制性能更好。然而，由于一些不确定性，例如未知的有效载荷，无法提前获得机械手的精确动力学模型。基于近似的控制器已经被设计来克服这种不确定性。诸多研究人员利用函数逼近工具来学习机器人动力学的非线性特性。神经网络由于其逼近能力而被广泛用于控制器设计。在[23]中，反向传播神经网络（BPNN）用于近似振动抑制装置模型中的未知非线性函数，而在[24]中，径向基函数神经网络（RBFNN）用于近似遥控机器人系统的未知非线性。与BPNN相比，RBFNN的学习过程是基于局部逼近的；因此，RBFNN可以避免陷入局部最优，并且具有更快的收敛速度。此外，RBFNN的隐层单元数量可以在训练阶段自适应调整，使神经网络更加灵活和自适应。因此，RBFNN更适合于实时控制的设计。

扫描二维码关注公众号，回复： 16962271 查看本文章

本文设计了一种基于神经网络的控制器来保证机械臂在关节空间中的跟踪性能，其中RBFNN用于近似机器人动力学的非线性函数。控制器的稳定性由李雅普诺夫稳定性理论保证。如图1所示，机器人学习系统由运动生成部分和轨迹跟踪部分组成。前者利用基于DMP的运动模型来学习和泛化运动技能；这些反过来又被表示为关节空间中的一组轨迹。后者采用自适应控制器来跟踪前者产生的轨迹，并引入RBFNN来补偿不确定的动力学。
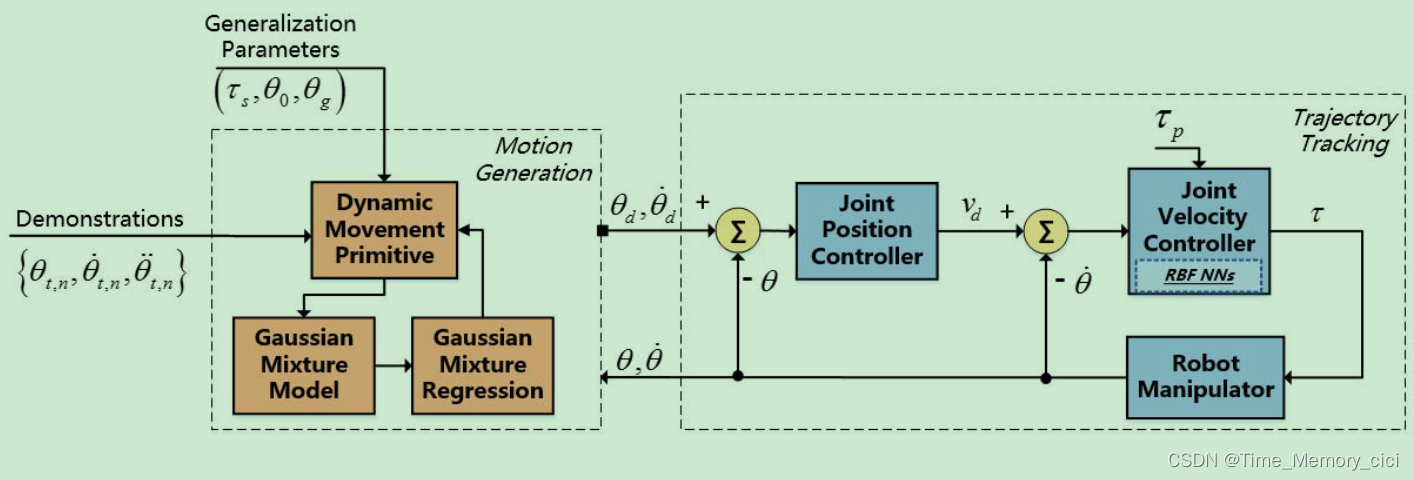
在这里插入图片描述
图1、所提系统的框图

本文提出了一个新颖而完整的机器人学习框架，该框架考虑了运动生成和轨迹跟踪的性能。2011年TRO的一篇论文提出的SEDS与本文基于DMP的模型相似。然而，保证SEDS稳定性的约束是由李雅普诺夫理论推导的，这增加了学习的复杂性。与仅考虑运动建模的[3]和[25]相比，本文提出的系统通过基于神经网络的控制器进行了增强，并且动态环境造成的影响可以通过神经学习来补偿。这种设计使机器人能够在现实世界中稳定、鲁棒地执行学习到的运动。

二、离散运动的基本模型

根据大脑的活动特性，运动技能可以分为点到点和周期性运动两种形式。当使用DS对运动进行建模时，这两种类型分别对应于点吸引子和极限环吸引子。本文关注的是点对点运动，并使用离散型DMP作为基本运动模型，该模型由弹簧-阻尼器系统和非线性函数组成。

DMP可以用于对关节空间或笛卡尔空间中的运动建模。两个空间中的运动被视为一组一维轨迹，每个轨迹被表示为一个DMP模型。为了简洁起见，本文只讨论关节空间中的运动建模问题。DMP模型定义如下[26]：

$\begin{aligned} \tau_{s} \dot{\xi}_{1} &=\xi_{2} \\ \end{aligned}$

$\begin{aligned} \tau_{s} \dot{\xi}_{2} &=l_{1}(\theta_{g}-\xi_{1})-l_{2}\xi_{2}+(\theta_{g}-\theta_{0}){\xi}_{3}f({\xi}_{3}) \end{aligned}\tag{1}$

$\begin{aligned} \tau_{s} \dot{\xi}_{3} &=-\alpha_{1}\xi_{3} \\ \end{aligned}\tag{2}$
这里的符号和我们看到的许多经典DMP论文不一样，但不影响，他们代表的含义是一摸一样的，只是换了个样子， $\xi_{1}\in R$ 表示关节位置， $\xi_{2}/\tau_{s} \in R$ 表示关节速度， $\dot{\xi}_{2}/\tau_{s}\in R$ 表示关节加速度。 $\xi_{3} > 0$ 为指数收敛的相位变量。 $l_{1}$ , $l_{2}$ 和 $\alpha_{1}$ 是正常数， $\theta_{0}$ 为起点， $\theta_{g}$ 为终点， $\theta_{g}-\theta_{0}$ 为空间缩放项， $\tau_{s}>0$ 为时间常数，非线性项 $f：R\rightarrow R$ 是相位变量 $\xi_{3}$ 的连续有界函数。

公式1是受非线性项扰动的弹簧-阻尼器系统。通常，我们选择 $l_{1}=l_{2}^2/4$ 以使前者具有临界阻尼特性。系统（2）的初始状态可以选择为 $\xi_{0}=1$ 。整个模型的稳定性是显而易见的；由于状态 $\xi_{3}$ 将收敛到零并且非线性函数 $f(\xi_{3})$ 是有界的，因此非线性项将收敛到0。然后，系统（1）成为稳定的弹簧-阻尼器系统，其状态收敛于目标 $\theta_{g}$ 。

原始弹簧阻尼器部分的大初始加速度（图2a）不适合机器人的实际运行。此外，加速度的较大变化将导致复杂的外力项，这不利于模型的学习。因此，本文将弹簧阻尼器部分中的目标点 $\theta_{g}$ 替换为另一个指数衰减系统的状态[27]

$\begin{aligned} \tau_{s} \dot{\xi}_{4} &=-\alpha_{2}(\xi_{4}-\theta_{g}) \\ \end{aligned}\tag{3}$
其中， $\alpha_{2}$ 是一个正常数， $\xi_{4}$ 的初始值设为 $\theta_{0}$ 。因此，系统1被重写为如下形式[27]：

$\begin{aligned} \tau_{s} \dot{\xi}_{1} &=\xi_{2} \\ \end{aligned}$

$\begin{aligned} \tau_{s} \dot{\xi}_{2} &=l_{1}(\xi_{4}-\xi_{1})-l_{2}\xi_{2}+(\theta_{g}-\theta_{0}){\xi}_{3}f({\xi}_{3}) \end{aligned}\tag{4}$

如图2（a）所示，修改后系统的加速度变得适中。 $f = 0$ 时系统（4）的演化如图2（b）所示。由于状态 $\xi_{4}$ 将收敛到 $\theta_{g}$ ，因此修改后的模型仍然稳定朝向目标点。

DMP模型因其简洁的公式和良好的泛化性而被选为基本的运动模型。由于DMP模型始终朝着 $\theta_{g}$ 稳定，因此可以通过调整 $\theta_{g}$ 和 $\theta_{0}$ 来对建模的运动进行空间缩放，而不会使模型失稳。空间缩放项( $\theta_{g}$ - $\theta_{0}$ )确保了运动的轮廓保持不变，并且可以通过调制 $\tau_{s}$ 来改变其持续时间。
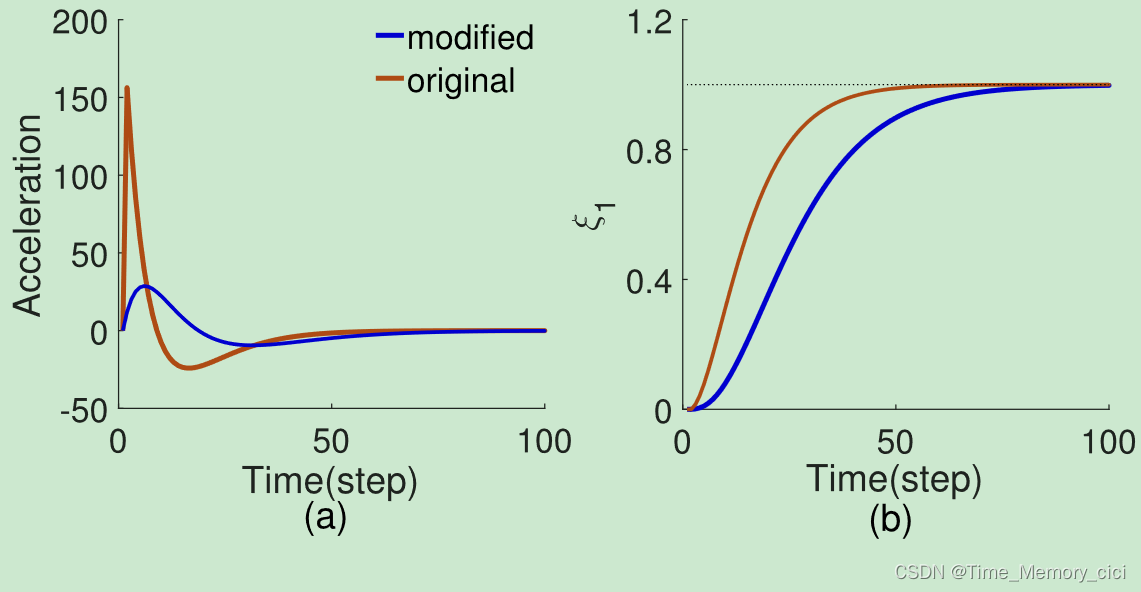
在这里插入图片描述
图2、（a）系统1中原始弹簧阻尼器部分和系统4中修改后DMP的加速度。（b）没有外力项（ $f = 0$ ）的系统（1）和（4）的演化。

三、学习运动模型

A、问题描述

DMP假设运动是由非线性动态系统（4）产生的，其不确定部分是非线性函数 $f({\xi}_{3})$ 。因此，DMP的学习问题是如何近似该函数，该函数补偿弹簧阻尼器部件的实际加速度和预期加速度之间的差异，以再现演示的运动（图3）。假设一维演示轨迹被记录并编码为时间序列 $\{(\theta_{t},\dot\theta_{t},\ddot\theta_{t})|t=1,2,\dots,T\}$ ，其中 $\theta_{t},\dot\theta_{t},\ddot\theta_{t}$ 分别描述了轨迹在 $t$ 时刻时的位置、速度和加速度， $T$ 是演示的持续时间，使用以下方程[26]计算 $t$ 时刻处 $f$ 的期望值：

$\begin{aligned} f_{t}=\frac{\tau^{2}_{s}\ddot \theta_{t}-[l_{1}(\xi_{4,t}-\theta_{t})-l_{2}\tau_{s}\dot \theta_{t}]} {(\theta_{T}-\theta_{1})\xi_{3,t}} \end{aligned}\tag{5}$

其中 $\xi_{3,t}和\xi_{4,t}$ 分别是 $t$ 时刻时的 $\xi_{3}和\xi_{4}$ 的值。等式（5）是复现的逆过程。由于 $f(\xi_{3})$ 是 $\xi_{3}$ 的函数，我们可以利用数据集 $\{(\xi_{3,t},f(t)|t=1,2,\dots,T\}$ 来近似该函数。

在原始DMP模型中，函数 $f(\xi_{3})$ 定义为[26]:
$\begin{aligned} f(\xi_{3})=\sum_{i=1}^{N_{s}} \gamma_{i} \phi_{i}\left(\xi_{3}\right) \end{aligned}\tag{6}$

其中 $\gamma_{i}\in R$ 是 $\phi_{i}(\xi_{3})$ 的权重， $\phi_{i}(\xi_{3})$ 是归一化高斯基函数，定义为：
$\begin{aligned} \phi_{i}\left(\xi_{3}\right)=\frac{\exp \left(-h_{i}\left(\xi_{3}-c_{i}\right)^{2}\right)}{\sum_{j=1}^{N_{s}} \exp \left(-h_{j}\left(\xi_{3}-c_{j}\right)^{2}\right)} \end{aligned}\tag{7}$

其中 $h_{i}>0$ 是第 $i$ 个高斯函数的宽度， $c_{i}>0$ 是第 $i$ 个高斯函数的中心； $N_{s}>0$ 是高斯函数的个数。有了这个公式，LWR可以用来学习模型。尽管如此，该解决方案仅适用于单个演示，并且多个演示将被编码为多个独立的DMP模型。因此，无法将多个特定任务的演示特征集成到一个DMP模型中。为了解决这个问题，引入GMM对中间数据进行建模，然后使用GMR对非线性函数进行估计。

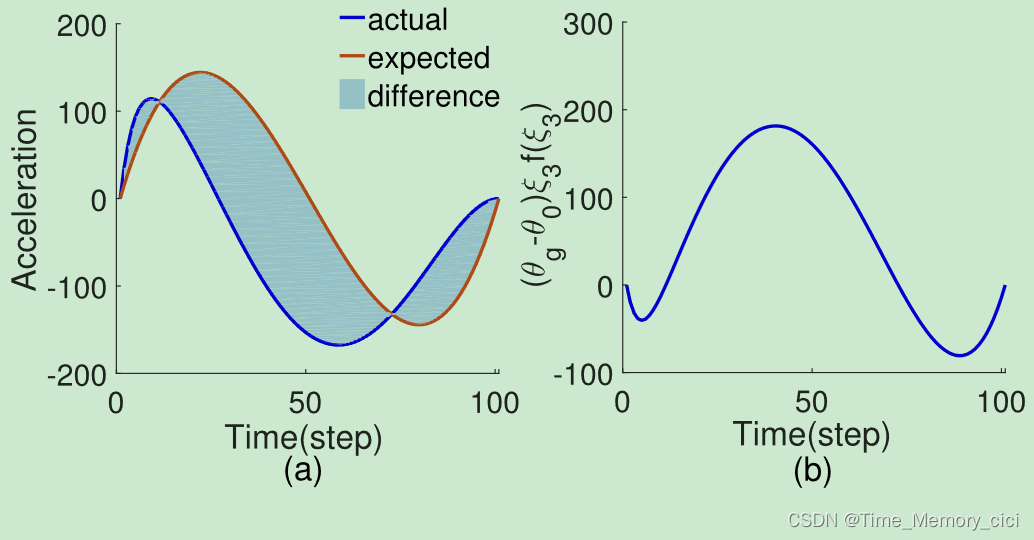
在这里插入图片描述
图3、（a）：弹簧减振器部分的实际加速度和再现演示的预期加速度（正弦曲线）。（b）：（a）中两个加速度之间的差，由非线性函数 $f({\xi}_{3})$ 补偿。

B、从多个演示中学习

给定特定任务的 $N_{d}$ 个演示 $\{(\theta_{t,n},\dot\theta_{t,n},\ddot\theta_{t,n})|t=1,2,\dots,T;n=1,2,\dots,N_{d}\}$ ，我们可以使用（5）获得数据集 $\{(\xi_{3,t},f_{t,n}|t=1,2,\dots,T;n=1,2,\dots,N_{d}\}$ 。然后，我们需要利用整个数据集来估计一个DMP模型的函数 $f({\xi}_{3})$ 。学习过程可以分解为两个步骤，如图4所示。为了简洁起见，我们使用 $\{\xi_{i},f_{0}\}$ 来表示数据集。
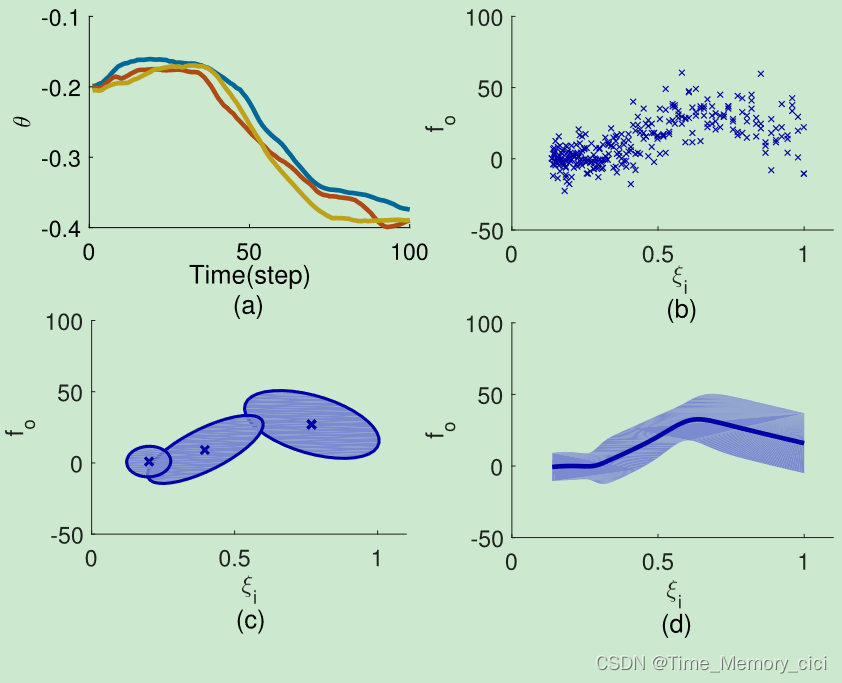
在这里插入图片描述
图4、（a）演示。（b）根据（a）计算数据集 $\{\xi_{i},f_{0}\}$ 。（c）数据集使用GMM进行编码。（d）使用GMR检索函数 $f({\xi}_{3})$ 的估计。
步骤一：使用GMM对数据集 $\{\xi_{i},f_{0}\}$ 进行编码。该模型假设数据集是由多个高斯分布生成的。GMM的联合概率密度定义如下[28]：

$\begin{aligned} p(\xi_{i},f_{0})=\sum^{K}_{K=1}\alpha_{k}\mathcal N (\xi_{i},f_{0};\mu_{k},\Sigma_{k}) \end{aligned}\tag{8}$
其中：
$\begin{aligned} \sum^{K}_{K=1}\alpha_{k}=1 \end{aligned}\tag{9}$

$\begin{aligned} \mu_{k}=\left[\begin{array}{l} \mu_{\xi_{i}, k} \\ \mu_{f_{o}, k} \end{array}\right], \quad \Sigma_{k}=\left[\begin{array}{cc} \Sigma_{\xi_{i}, k} & \Sigma_{\xi_{i} f_{o}, k} \\ \Sigma_{f_{o} \xi_{i}, k} & \Sigma_{f_{o}, k} \end{array}\right] \end{aligned}\tag{10}$
并且 $\mathcal N$ 是如下定义的高斯概率分布：

$\begin{aligned} \begin{array}{l} \mathcal{N}(\xi_{i}, f_{o} ; \mu_{k}, \Sigma_{k}) \\ \quad=\frac{\exp \left[-0.5\left(\left[\xi_{i}, f_{o}\right]^{T}-\mu_{k}\right)^{T} \Sigma_{k}^{-1}\left(\left[\xi_{i}, f_{o}\right]^{T}-\mu_{k}\right)\right]}{2 \pi \sqrt{\left|\Sigma_{k}\right|}} \end{array} \end{aligned}\tag{11}$

这里， $K$ 是高斯分布的个数， $\alpha_{k} \ge0$ 是权重， $\mu_{k}\in R^{2\times 1}$ 和 $\Sigma_{k}\in R^{2\times 2}$ 表示第 $K$ 个高斯分量的均值和协方差矩阵。

$\alpha_{k},\mu_{k},\Sigma_{k}$ 是要学习的参数。我们可以使用以下步骤从给定的数据集中估计它们的值并学习GMM。

1)参数初始化：用于参数估计的期望-最大化（EM）算法对初始值敏感。因此，k-means算法[29]用于初始化未知参数 $\alpha_{k},\mu_{k},\Sigma_{k}$ 。该算法将数据集划分为多个集，旨在找到一个分区 $D=\{ {D_{1}，D_{2}，…，D_{K}}\}$ 以最小化每个集的平方偏差之和[29]

$\begin{aligned} \hat{D}=\underset{D}{\arg \min } \sum_{k=1}^{K} \sum_{x \in D_{k}}\|x-m_{k}\|^{2} \end{aligned}\tag{12}$

其中， $x=[x_{1}，x_{2}]^T\in R^{2×1}$ 是对应于 $[\xi_{3,t}，f_{t,n}]^T$ 的数据向量， $m_{k}\in R^{2\times 1}$ 是分布在 $D_{k}$ 和 $\cup_{k=1}^{K}D_{k}=\{\xi_{i},f_{0}\}$ 中的数据的平均值。该算法重复分配和更新步骤，直到该分区不再更改为止。然后，将未知参数的初始值指定为[14]：
$\begin{aligned} \alpha_{k} & =\frac{\left|D_{k}\right|}{\sum_{i=1}^{K}\left|D_{i}\right|} \end{aligned}\tag{13}$

$\begin{aligned} \mu_{k} & =m_{k}, \quad \Sigma_{k}=\left[\begin{array}{cc} \Sigma_{x_{1}} & \Sigma_{x_{1} x_{2}} \\ \Sigma_{x_{2} x_{1}} & \Sigma_{x_{2}} \end{array}\right]_{x \in D_{k}} \end{aligned}\tag{14}$
2) 参数估计：EM算法是估计GMM参数的合适方法。该算法旨在找到参数 $\pi_{k}=(\alpha_{k},\mu_{k},\Sigma_{k})$ ，以最大化对数似然函数[30]

$\begin{aligned} \hat\pi_{k}=\underset{\pi_{k}}{\arg \max}\log(p(\xi_{k},f_{0}|\pi_{k})) \end{aligned}\tag{15}$
3) 模型选择：高斯分量的数量将影响GMM的拟合表现。如果选择更多的组件，GMM可以更好地表示数据集，但它可能导致过拟合和过多的参数。使用贝叶斯信息准则（BIC）来确定组件的数量，从而达到折衷。BIC分数定义如下[14]：
$\begin{aligned} S_{B I C}(K)=-2 \log \left(p\left(\xi_{i}, f_{o} \mid \pi_{k}\right)\right)+(6 K-1) \log \left(N_{d}\right) \end{aligned}\tag{16}$

其中 $N_{d}$ 是数据集的大小， $K$ 表示分量的数量。组件的数量最终选择为 $K_{ms}=\arg \min S_{BIC}(K)$ ，并且 $K_{ms}$ 的上限由设计者确定。

步骤二：使用GMR来估计函数 $f(\xi_{3})$ 。根据[28]，概率密度（8）可以重写为：
$\begin{aligned} p\left(\xi_{i}, f_{o}\right)=\sum_{k=1}^{K} \alpha_{k} \mathcal{N}\left(f_{o} ; \hat{\eta}_{k}, \hat{\sigma}_{k}^{2}\right) \mathcal{N}\left(\xi_{i} ; \mu_{\xi_{i}, k}, \Sigma_{\xi_{i}, k}\right) \end{aligned}\tag{17}$

其中，
$\begin{aligned} \hat{\eta}_{k}\left(\xi_{i}\right)=\mu_{f_{o}, k}+\Sigma_{f_{o} \xi_{i}, k}\left(\Sigma_{\xi_{i}, k}\right)^{-1}\left(\xi_{i}-\mu_{\xi_{i}, k}\right) \end{aligned}\tag{18}$
和
$\begin{aligned} \begin{array}{c} \hat{\sigma}_{k}^{2}=\Sigma_{f_{o}, k}-\Sigma_{f_{o} \xi_{i}, k}\left(\Sigma_{\xi_{i}, k}\right)^{-1} \Sigma_{\xi_{i} f_{o}, k} \\ \end{array} \end{aligned}\tag{19}$

$\xi_{i}$ 的边缘密度计算如下[28]：
$\begin{aligned} p\left(\xi_{i}\right)&=\int p\left(\xi_{i}, f_{o}\right) d f_{o} \\ &=\sum_{k=1}^{K} \alpha_{k} \mathcal{N}\left(\xi_{i} ; \mu_{\xi_{i}, k}, \Sigma_{\xi_{i}, k}\right) \\ \end{aligned}\tag{20}$

根据（17）和（20），给定 $\xi_{i}$ 的 $f_{0}$ 的条件概率密度为
$\begin{aligned} p\left(f_{o} \mid \xi_{i}\right)=\sum_{k=1}^{K} \beta_{k}\left(\xi_{i}\right) \mathcal{N}\left(f_{o} ; \hat{\eta}_{k}, \hat{\sigma}_{k}^{2}\right) \end{aligned}\tag{21}$

其中，
$\begin{aligned} \beta_{k}\left(\xi_{i}\right)=\frac{\alpha_{k} \mathcal{N}\left(\xi_{i} ; \mu_{\xi_{i}, k}, \Sigma_{\xi_{i}, k}\right)}{\sum_{k=1}^{K} \alpha_{k} \mathcal{N}\left(\xi_{i} ; \mu_{\xi_{i}, k}, \Sigma_{\xi_{i}, k}\right)} \\ \end{aligned}\tag{22}$
然后，我们可以得到如下的GMR函数[28]：
$\begin{aligned} R\left(\xi_{i}\right)=E\left(f_{o} \mid \xi_{i}\right)=\sum_{k=1}^{K} \beta_{k}\left(\xi_{i}\right) \hat{\eta}_{k}\left(\xi_{i}\right) \\ \end{aligned}\tag{23}$
此外，函数 $f(\xi_{3})$ 的估计为：
$\begin{aligned} \begin{array}{l} \hat{f}\left(\xi_{3}\right)=\sum_{k=1}^{K} \beta_{k}\left(\xi_{3}\right) \hat{\eta}_{k}\left(\xi_{3}\right) \end{array} \end{aligned}\tag{24}$

与（6）相比，该估计乘以附加项 $\hat{\eta}_{k}\left(\xi_{3}\right)$ ；因此，该方法使运动模型能够从多个演示中提取更多的特征。

四、机械臂的自适应神经控制（第四部分留到以后更新，其他内容全）

在实践中，机器人必须与各种有效载荷相互作用。为了考虑未知载荷对机械手动力学的影响，设计了一种基于神经网络的控制器来跟踪关节空间中运动模型生成的参考轨迹。

A、动力学描述

具有n连杆的机械臂动力学描述如下：
$\begin{aligned} M(\theta)\ddot \theta+C(\theta, \dot\theta)\dot\theta+G_{0}(\theta)+\tau_{p}=\tau \end{aligned}\tag{25}$
其中， $\theta \in R^n,\dot\theta \in R^n,\ddot\theta \in R^n$ 为关节位置，关节速度和关节加速度， $\tau$ 为控制力矩， $\tau_{p}$ 为有效载荷引起的力矩， $M(\theta) \in R^{n \times n} ,C(\theta, \dot\theta)\in R^{n},G_{0}(\theta)\in R^{n}$ 和传统机械臂动力学公式定义一样，分别表示对称正定的的惯性矩阵，科里奥利和向心力矩矩阵，以及重力矢量。根据[31]，矩阵 $M, C, G$ 满足

$\begin{aligned} s^{T}(\dot M-2C)s=0, \forall s\in R^{n} \end{aligned}\tag{26}$

B、RBF神经网络

RBFNN是逼近任何连续函数 $R^{m} \rightarrow R$ 的有效工具，如下所示[32]：
$\begin{aligned} g(\vartheta)=W^{T} S(\vartheta)+\varepsilon(\vartheta), \quad \forall \vartheta \in \Omega_{\vartheta} \end{aligned}\tag{27}$

其中 $\vartheta \in \Omega_{\vartheta} \subset R^{m}$ 表示输入向量， $W=[\omega_{1},\omega_{2},\cdots,\omega_{N} ]^{T} \in R^{N}$ 为神经网络权重向量，近似误差 $\varepsilon(\vartheta)$ 是有界的， $S(\vartheta)=[s_{1}(\vartheta),s_{2}(\vartheta),\cdots,s_{N}(\vartheta)]$ 为非线性向量函数，其中 $s_{i}(\vartheta)$ 定义为高斯函数：

$\begin{aligned} s_{i}(\vartheta)=\exp \left[-\frac{\left(\vartheta-\kappa_{i}\right)^{T}\left(\vartheta-\kappa_{i}\right)}{\chi_{i}^{2}}\right], i=1,2, \ldots, N \end{aligned}\tag{28}$

其中 $\kappa_{i}=[\kappa_{i1},\kappa_{i2},\dots,\kappa_{im}]^{T} \in R^{m}$ 表示高斯函数的中心， $\chi_{i}^{2}$ 是高斯函数的方差，理想的权重向量定义如下：
$\begin{aligned} W=\underset{\hat{W} \in R^{N}}{\arg \min }\left\{\sup _{\vartheta \in \Omega_{\vartheta}}\left|g(\vartheta)-\hat{W}^{T} S(\vartheta)\right|\right\} \end{aligned}\tag{29}$

对于所有的 $\vartheta \in \Omega_{\vartheta}$ ，使得近似误差最小化。

C、控制设计

控制器设计包括关节位置控制器和关节速度控制器的设计，如图1所示。在后者中使用RBFNN来近似不确定动力学。
1）关节位置控制器：关节位置跟踪误差定义为 $e_{p}=[e_{p1},e_{p2},\cdots,e_{pn}]^{T}=\theta-\theta_{d}$ ，其中 $\theta_{d}=[\theta_{d1},\theta_{d2},\cdots,\theta_{dn}]^{T} \in R^{n}$ 是参考轨迹，它是光滑的和有界的。误差变换函数[33]介绍如下：
$\begin{aligned} e_{p i}(t)=\delta(t) H_{i}\left(L_{i}\left(\frac{e_{p i}(t)}{\delta(t)}\right)\right), \quad i=1,2, \ldots, n \end{aligned}\tag{30}$
其中 $\delta(t)=(\delta_{0}-\delta_{\infty})e^{-at}+\delta_{\infty}$

五、实验

所提出的系统通过两组实验进行了测试：基于神经网络的控制器测试和基于DMP的运动模型测试。

A、基于神经网络的控制器测试

在这组实验中，测试了神经网络学习的性能，它补偿了有效载荷引起的机械手动力学的不确定性。实验是在具有两个七自由度机械臂的Baxter机器人上进行的。本文将从肩部到末端执行器的关节命名为 $s 0 、 s 1 、 e 0 、 e 1 、 w 0 、 w 1 和 w 2$ 。有效载荷使用机器人的左夹爪连接，该夹爪重0.94 kg。机器人需要跟踪圆形轨迹，定义为: $[X,Y,Z]=[0.65+0.1sin(2\pi t/4),0.2+0.1cos(2\pi t/d),0.2](m)$ ，姿态固定。通过逆运动学获得关节空间中相应的轨迹，并将其作为控制器的输入。

我们为神经网络的每个输入维度选择三个节点，节点的中心在关节位置和关节速度的限制内均匀分布。有 $N ＝ 2187$ 个神经网络节点被选择用于 $\hat M(\theta)$ 和 $\hat G(\theta)$ ， $2 N$ 个节点被选择为 $\hat C(\theta, \dot \theta)$ ， $4 N$ 个节点被选为 $\hat r(\theta, \dot \theta,v_{d},\dot v_{d})$ 。此外，神经网络权重矩阵初始化为 $\hat W_{M}=0 \in R^{nN \times n},\hat W_{C}=0 \in R^{2nN \times n},\hat W_{G}=0 \in R^{nN \times n}和 \hat W_{r}=0 \in R^{4nN \times n}$ ，其中 $n = 7$ 。误差变换函数的参数设置为 $\delta_{0}=0.2，\delta_{\infty}=0.04，a=1，\sigma=1$ 。

在第一个实验中，使用没有神经网络学习的控制器控制机械臂，并记录实际的关节角度。然后，在第二个实验中，使用所提出的神经网络学习的控制器来控制机械手。两个实验中的参考和实际关节角度如图6所示，相应的跟踪误差如图7所示。（ 图6和图7就不贴出来了，具体可以看原文，主要体现了使用神经网络控制器后，七个关节的跟踪误差更小）当不使用神经网络时，跟踪误差相对较高，这是由于末端执行器夹持的有效载荷引起的，而在第二个实验中，机械手的每个关节都很好地跟踪参考轨迹，并且随着补偿扭矩的增加，所有跟踪误差都减少到区间[-0.04，0.04]（rad），如图8（a）所示。机械手动力学的重力项是有效载荷影响的主要部分，因此，我们特别显示了图8（b）中 $\hat W_{G}$ 每列的范数。我们可以看到，由于神经网络产生的转矩仍然不能补偿未知动力学的影响，因此权重矩阵的每个列向量的范数都会递增。然而，所有范数的上升速度都随着扭矩补偿的增加而降低。

B、基于DMP的运动模型测试

第二组实验旨在验证基于DMP的运动模型。测试了泛化能力和学习表现。在这些实验中，通过引导机械臂操作来进行演示。

1)泛化能力

在这个实验中，示教者演示如何将水倒入放在桌子上的杯子中，如图9所示。演示过程重复五次。关节 $w 0 、 w 1 、 s 0 和 e 1$ 移动，而其他关节固定。关节角度被记录并用于学习修改后的DMP。DMP模型的参数设置为 $\tau_{s}=1，l_{1}=25，l_{2}=10，\alpha_{1}=\alpha_{2}=8$ 。
在这里插入图片描述
图9、倒水演示

学习结果如图10所示(我就不贴出来了)。从演示中再现了四个关节的运动，综合了这些演示的特点，使机器人能够成功完成倒水任务。随后，运动的目标被修改为向另一个杯子倒水。如图11所示（图11不贴出来了，看原文），每个关节角度的运动轨迹收敛到新的目标，并且保留了每个再现的轮廓。作者在机器人上测试了复现运动和泛化运动。如图12（a）所示，机器人成功完成了倒水任务，如图12的（b）所示的，机器人可以将水倒进另一个杯子中。

1)学习表现

为了进一步验证基于DMP的运动模型的学习表现，作者为机器人设计了一个绘图任务；实验设置如图13（a）所示（不贴图了）。在这里，在示教者演示任务五次后，机器人需要在纸上绘制正弦曲线的图像。如图13（b）所示，演示是有缺陷的，曲线是不规则的。其中一个原因是演示者通过握住机器人的手腕来间接地在本文上绘图，这影响了绘图技巧的发挥。演示在任务空间中建模，机器人在学习后执行绘图任务（图14）。如图15（a）所示，在多次演示的情况下，运动模型再现了平滑曲线。我们还可以看到，由于传感器的测量误差，记录的轨迹发生了失真。如图15（b）所示，机器人绘制的曲线比演示的曲线更平滑，从而验证了基于DMP的运动模型的学习性能。
在这里插入图片描述
图15（b）、绘图结果，蓝色曲线是机器人在学习后绘制的。

六、Conclusion

本文开发了一种由运动生成和轨迹跟踪组成的新型机器人学习系统。由于DMP模型的泛化能力，素以选择它作为运动模型的基础。为了提高学习性能，采用GMM和GMR来估计运动模型的非线性函数。通过这种修改，该模型可以从特定任务的多次演示中提取更多的运动特征，并生成合成这些附加特征的运动。此外，设计了一个基于神经网络的控制器来克服未知有效载荷的影响，使机械臂能够更准确地跟踪生成的运动。所提方法在Baxter机器人上进行了实验验证，以测试本文提出的方法的性能，这些方法可以用于促进更高水平的机器人学习。在未来的工作中，我们将进一步将强化学习融入我们的系统，以提高机器人的学习能力。