2023.07.03 在研究OTFS的过程中,不得不与目前的老大哥OFDM进行对比,在这过程中,发现自己对于OFDM调制方式的理解还浮于表面,因此给自己挖个坑,建立此帖,不定期更新,记录一下对于OFDM从无到有的理解,欢迎大家一起学习交流。
前言
研究OTFS的过程中,免不了需要与OFDM进行比较,在这一过程中,难免会产生以下疑问,比如:为什么在高移动性场景下OFDM误码性能很差?尽管OFDM具有许多缺点比如PAPR高OOB泄露,在4G、5G甚至埃隆马斯克的星链中得到了广泛应用?它们是如何规避这些不足的?……如果你也有这些疑问,请耐心看下去吧,祝你有一个愉快的学习旅程~
一、如何理解OFDM中的"O"?
OFDM (Orthogonal frequency-division multiplexing, 正交频分复用) 是一种多载波调制技术。其核心思想是将宽频率载波划分成多个带宽较小的正交子载波,如下图所示,并使用这些正交子载波发送及接收信号。因此,”O“主要表示子载波间具有正交性,那么如何理解其正交性呢?与FDM相比其优势是什么呢?其中的数学原理又是什么呢?请继续往下看(doge)
1.1 子载波正交性的意义
1.1.1 子载波的正交性

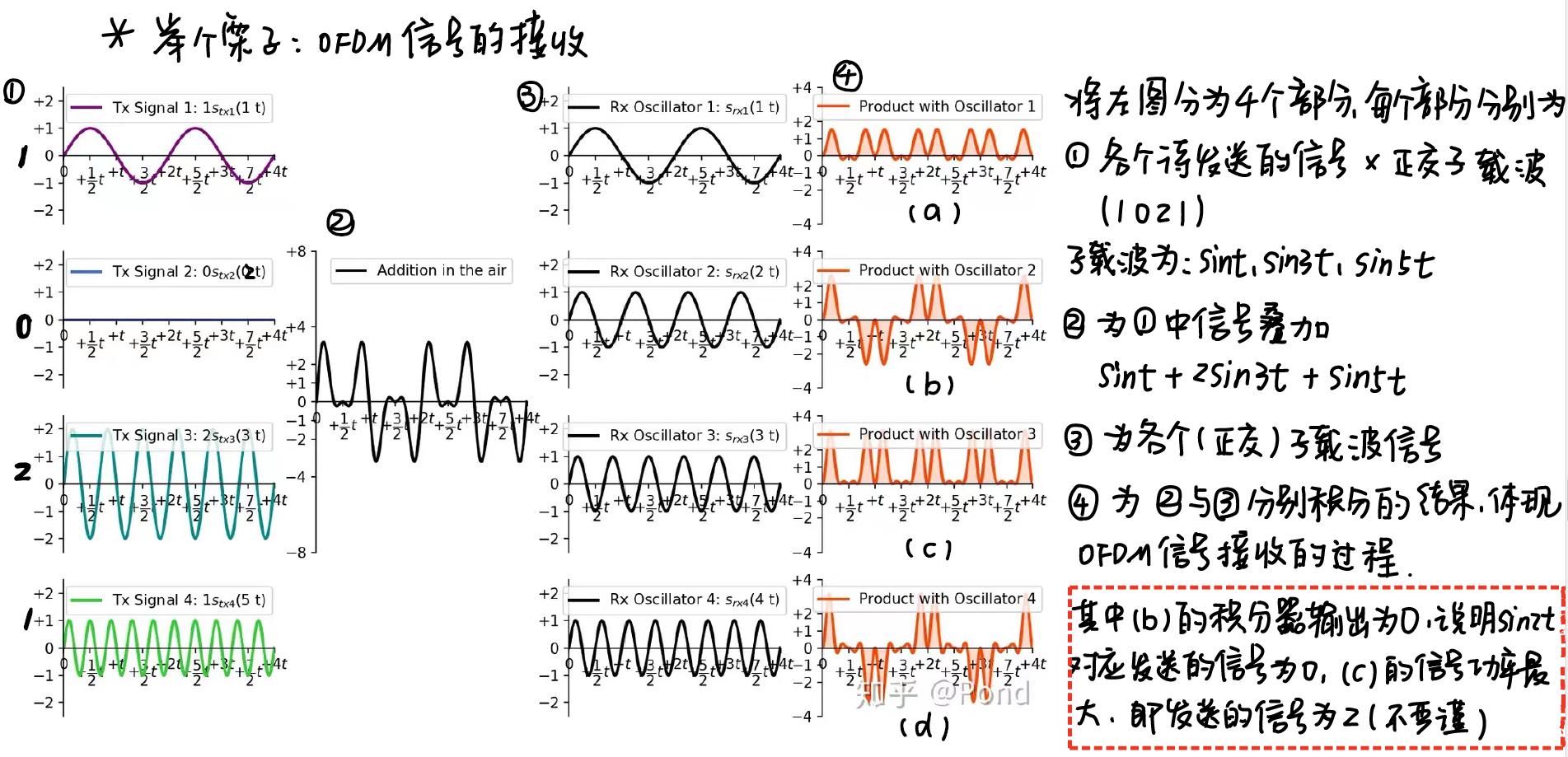
1.1.2 举个栗子:OFDM信号的接收

1.2 如何实现子载波的正交性
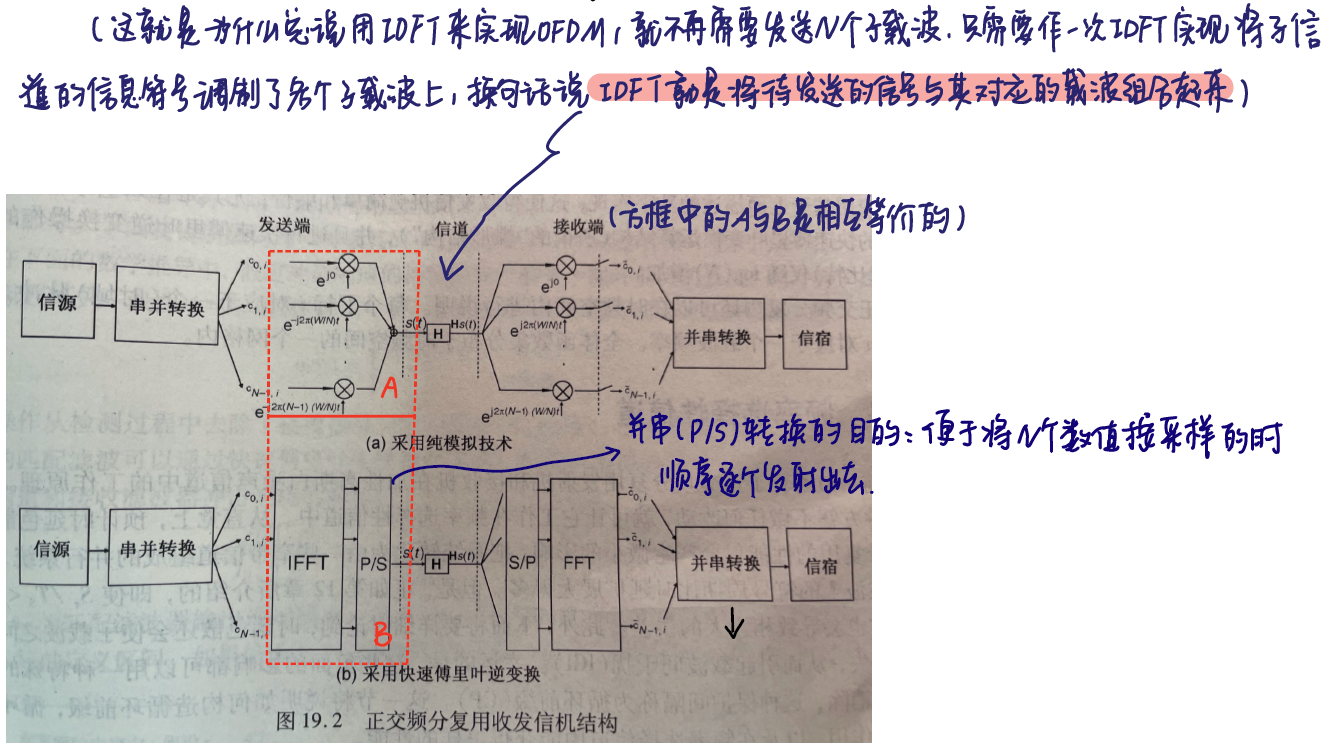
1.2.1 如何实现多载波信号的发射——神奇的IFFT

1.3 从FDM到OFDM

1.4 从频域理解OFDM
一直不太理解:从频域来看为什么OFDM是多个sinc函数叠加的形式?(比如像下图这样子)

从时域来看(此时只研究单个子载波),调制为某个正弦载波信号与一个码元波形(就是数字基带传输的矩形波,如NRZ等,可以看成是某个门函数)的乘积;将上述调制过程转到频域(傅里叶变化如下),频域上体现的是对sinc函数的搬移。

1.5 从DFT到FFT
在数字信号处理领域中,离散傅里叶变换(DFT)与数字滤波是功能强大的两种变换,DFT是用来分析离散信号序列(可以理解为连续信号在时域周期采样得到的一组值)的谐波、频率和内容的一套数学方法,其表达式可以写成:
X ( m ) = ∑ n = 0 N − 1 x ( n ) e − j 2 π n m / N (2) X\left(m\right)=\sum_{n=0}^{N-1}x\left(n\right)e^{-j2\pi nm/N}\tag{2} X(m)=n=0∑N−1x(n)e−j2πnm/N(2)
接着将拆成奇、偶两部分:
KaTeX parse error: Expected 'EOF', got '}' at position 26: …{n=0}^{(N/2)-1}}̲x\left(n\right)…
将公式第二部分中相位角为常数的部分提到前面,整理可得:
X ( m ) = ∑ n = 0 ( N / 2 ) − 1 x ( 2 n ) W N 2 n m + W N m ∑ n = 0 ( N / 2 ) − 1 x ( 2 n + 1 ) W N 2 n m (4) X(m)=\sum_{n=0}^{(N/2)-1}x(2n)W_{N}^{2nm}+W_{N}^{m}\sum_{n=0}^{(N/2)-1}x(2n+1)W_{N}^{2nm}\tag{4} X(m)=n=0∑(N/2)−1x(2n)WN2nm+WNmn=0∑(N/2)−1x(2n+1)WN2nm(4)
其中, W N = e − j 2 π / N W_{N}=e-j2\pi/N WN=e−j2π/N,由于 W N 2 = e − j 2 π 2 / N = e − j 2 π / ( N / 2 ) W_{N}^{2}=e^{-j2\pi2/N}=e^{-j2\pi/(N/2)} WN2=e−j2π2/N=e−j2π/(N/2),因此可以用 W N / 2 W_{N/2} WN/2代替 W N 2 W_{N}^{2} WN2,继续整理可得:
X ( m ) = ∑ n = 0 ( N / 2 ) − 1 x ( 2 n ) W N / 2 n m + W N m ∑ n = 0 ( N / 2 ) − 1 x ( 2 n + 1 ) W N / 2 n m (5) X(m)=\sum_{n=0}^{(N/2)-1}x(2n)W_{N/2}^{nm}+W_{N}^{m}\sum_{n=0}^{(N/2)-1}x(2n+1)W_{N/2}^{nm}\tag{5} X(m)=n=0∑(N/2)−1x(2n)WN/2nm+WNmn=0∑(N/2)−1x(2n+1)WN/2nm(5)
从 n n n的范围可以看出与式 ( 2 ) (2) (2)相比减少了一半的计算量。此时,令 m + N / 2 = m m+N/2=m m+N/2=m继续整理可以发现:
X ( m + N / 2 ) = ∑ n = 0 ( N / 2 ) − 1 x ( 2 n ) W N / 2 m − W N m ∑ n = 0 ( N / 2 ) − 1 x ( 2 n + 1 ) W N / 2 n m (6) X(m+N/2)=\sum_{n=0}^{(N/2)-1}x(2n)W_{N/2}^{m}-W_{N}^{m}\sum_{n=0}^{(N/2)-1}x(2n+1)W_{N/2}^{nm}\tag{6} X(m+N/2)=n=0∑(N/2)−1x(2n)WN/2m−WNmn=0∑(N/2)−1x(2n+1)WN/2nm(6)
式 ( 6 ) (6) (6)与式 ( 5 ) (5) (5)相比只差一个负号,仅改变旋转因子 W N m W_N^m WNm的符号,并利用 X ( m ) X(m) X(m)的求和结果就可以得到 X ( m + N / 2 ) X(m+N/2) X(m+N/2)。因此,可以用两个 N / 2 N/2 N/2点的DFT得到一个 N N N点的DFT,假设N=8则可以拆成两个4点的DFT进行计算:
 依照上述思路,可以将4点的DFT继续拆成两个2点的DFT:
依照上述思路,可以将4点的DFT继续拆成两个2点的DFT:

总结:FFT并不是DFT的近似,它是一种减少了必要四则运算数量的DFT,具体而言,FFT严格等于DFT。因此,DFT具有的特点,比如输出对称性,线性,输入振幅,泄露以及扇形损耗,FFT都有与其相同的性质。
1.6 本节参考
[1] 知乎好文:OFDM(正交频分复用)技术
[2] 小白必看:给“小白”图示讲解OFDM的原理
[3] 如何提取信号:直观图解OFDM原理
[4] 数字信号处理(第三版)作者: Richard G.Lyons (理查德 G.莱昂斯) 著 , 张建华 译 , 许晓东 译 , 孔松林 译
二、有空继续更……
三、总结
为了仔细领悟其推导过程,本节关键部分全程本人手写完成,如有不清晰的地方请私信我,我会进行修改与更正,欢迎大家多多批评指正。