机器学习 第四课 线性回归
概述
线性回归 (Linear Regression) 是统计学和机器学习 (Machine Learning) 中的基石. 从最简单的单一变量的线性回归到更复杂的多变量线性回归, 该方法为我们提供了一种强大的工具, 可以理解数据中的关系, 并进行有根据的预测.

在本篇文章中, 小白我讲带领大家详细介绍回归的基础理论, 并通过 Python 的实际案例来展示. 无论是机器学习的初学着还是希望对线性回归有一个更深的了解, 本文都会提供见解和指导.
什么是线性回归?
线性回归 (Linear Regression) 是机器学习领域使用最广泛和最广为人知的算法之一. 线性回归是一种估计连续边拉你个之间关系的方法. 例如, 放假预测, 如果我们指导过去的放假以及与之相关的各种因素 (房屋面积, 建筑年代等), 我们就可以使用线性回归来预测未来的房价.
关键概念
因变量
因变量 (Dependent Variable) 因变量是我们要预测的变量, 是我们关心的主要目标.
举个栗子, 我们要预测房价, 那么房价就是因变量 (Dependent Variable). 我们需要通过 (房屋面积, 建筑年份等) 因素 (特征) 来预测.
正确的因变量是任何回归分析的第一步, 这确保我们知道我们的目标是什么, 以及如何衡量是否成功.
自变量
自变量 (Independent Variable) 是我们用来预测因变量 (Dependent Variable) 的变量. 自变量会影响因变量, 但不受因变量的影响.
举个栗子: 在预测房价的例子中, 房屋面积, 位置, 是否接近学校, 建筑年份等都是自变量 (Independent Variable), 这些都是可能影响房价的因素.
选择正确的自变量是确保线性回归 (Linear Regression) 模型有效性的关键. 如果我们选择了不相关或冗余的自变量, 模型会表现不佳, 而且也会更难解释模型的结果.
线性关系
线性回归 (Linear Regression) 的核心思想是使用最佳拟合直线来描述自变量和因变量的关系, 这条线也被称为回归线. 在线性回归中, 我们假设自变量和因变量之间的关系是线性的, 这意味着改变自变量会导师因变量线性的变化.
找到一个能够描述数据点分布的直线对于预测和解释关系至关重要. 这条线称为最佳拟合线, 尽可能减少了每个数据点到直线的距离, 这些距离被称为偏差 (Bias).
公式:
y = w x + b y = wx + b y=wx+b
下面是一个简单案例:
数据: 工资和年龄 (2 个特征)
目标: 预测银行会贷款给我多少钱 (标签)
| 工资 | 年龄 | 额度 |
|---|---|---|
| 4000 | 25 | 20000 |
| 8000 | 30 | 70000 |
| 5000 | 28 | 35000 |
| 7500 | 33 | 50000 |
| 12000 | 40 | 85000 |
工资和年龄都会影响最终银行贷款的结果. 那么它们各自有多大的影响呢?
X1, X2 代表我们的两个特征: 年龄和工资. Y 代表银行最终会借给我们多少钱.
找到最合适的一条线 (想象一个高维 ) 来最好的拟合我们的数据点. 如下图所示:
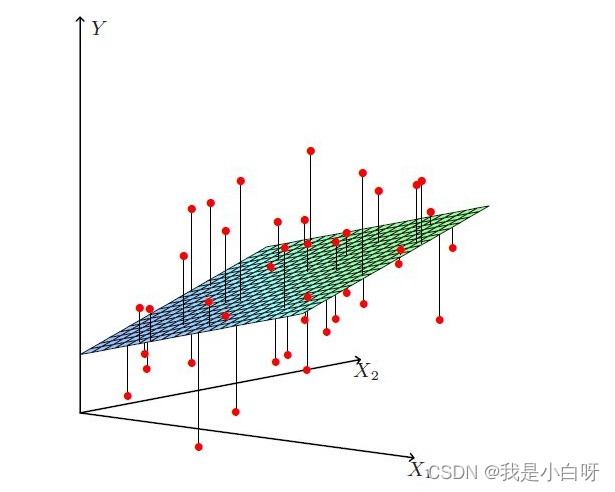
基本的线性方程
表达式理解
y = w 0 + w 1 x 1 + w 2 x 2 y =w_0 + w_1x_1 + w_2x_2 y=w0+w1x1+w2x2
- w 0 w_0 w0为偏置顶, 相当于 C
- x1, x2 是自变量 (Dependent Variable), 即用于预测的因子
- y y y 是因变量 (Independent Variable), 即我们想要预测的值
- w 1 w_1 w1, w 2 w_2 w2 为斜率, 表示当 x1, x2 每增加一个单位, y 预期值变化的数值
线性模型, 中的向量 w 值. 客观的表达了各属性在预测中的重要性, 因此线性模型有很好的解释性. 对于这种 “多特征预测” 也就是 (多元线性回归), 那么线性回归就是在这个基础上得到这些 w 的值. 然后以这些值来建立模型, 预测试数据. 简单的来说就是学得一个线性模型以尽可能准确的预测实际输出标记.
那么如果对于多变量线性回归来说我们可以通过向量的方式来表示 θ 值与特征 X 值之间的关系:
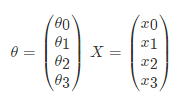
两向量相乘, 结果为一个整数是估计值. 其中所有特征集合的第一个特征值 x 0 = 1 x_0=1 x0=1, 那么我们可以通过通用的向量公式来表示性模型:
h θ ( x ) = ∑ i = 0 n θ i x i = θ T x h_\theta(x)=\sum\limits_{i=0}^{n}\theta_ix_i = \theta^Tx hθ(x)=i=0∑nθixi=θTx
多变量回归
在多变量线性回归中, 拥有多个变量. 方程可以表示为:
y = w 0 + w 1 x 1 + w 2 x 2 + w 3 x 3 + . . . + w n x n y = w_0 + w_1x_1 + w_2x_2 + w_3x_3 + ... + w_nx_n y=w0+w1x1+w2x2+w3x3+...+wnxn
在上述公式中, 我们有 n 个自变量, 并且每个都有对应的系数 (权重). 这允许我们在模型中考虑更多的影响因子, 从而提高预测的精确性.
误差项和损失函数
误差项
当模型无法完美地拟合所有的数据点, 主要是因为数据中存在的噪声或为观察到的影响因子. 误差项可以帮助我们量化这种不确定性.
均方误差 (MSE)
MSE (Mean Square Error) 是评估莫模型性能的一个关键指标. MSE 是衡量预测值与实际值之间的差异大小.
公式:
M S E = 1 n ∑ i = 1 n ( y i − y ˆ i ) 2 MSE = \frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \^y_i)^2 MSE=n1i=1∑n(yi−yˆi)2
- y i y_i yi: 是实际值
- y ˆ i \^y_i yˆi: 是预测值
MSE 越小意味着模型的精确性越高.
最小二乘法
什么是最小二乘法
最小二乘法 (Least Squares) 是统计学和数值分析中的一种经典方法, 被广泛应用于回归分析和曲线拟合中. 最小二乘法的核心思想是基于一个明确的标准来确定位置的参数. 确保模型对训练数据的预测误差的平方和最小.
公式:
S = ∑ i = 1 n ( y i − ( w 0 + w 1 x 1 ) ) 2 S = \sum\limits_{i=1}^{n}(y_i -(w_0 + w_1x_1))^2 S=i=1∑n(yi−(w0+w1x1))2
最小二乘法思想
考虑一下最简单的线性回归模式, 模型为:
y = w 0 + w 1 x 1 y =w_0 + w_1x_1 y=w0+w1x1
我们的目标是最小化误差平方和:
S = ∑ i = 1 n ( y i − ( w 0 + w 1 x 1 ) ) 2 S = \sum\limits_{i=1}^{n}(y_i -(w_0 + w_1x_1))^2 S=i=1∑n(yi−(w0+w1x1))2
我们需要找到使得 S 值最小的 w0 和 w1 分别求偏导, 并将它们设置为 0. 这会得到一组方程, 通过求解方程, 我们可以分别得到 w0 和 w1, 这些值就是使得误差平方达到最小的值.
详细推导
对 w0 求偏导
为了求 S 关于 w0 的偏导, 我们需要使用连式法则, 平方的导数 ( u 2 ) ′ = 2 u d u = 2 u (u^2)' = 2udu = 2u (u2)′=2udu=2u:
∂ S ∂ w 0 ( y i − ( w 0 + w 1 x 1 ) ) 2 = 2 ( y i − w 0 − w 1 x 1 ) d ( − w 0 ) = 2 ( y i − w 0 − w 1 x 1 ) × ( − 1 ) = 2 ( w 0 + w 1 x 1 − y i ) \frac{\partial S}{\partial w_0} (y_i -(w_0 + w_1x_1))^2\\= 2(y_i - w_0 - w_1x_1)d(-w_0) \\= 2(y_i - w_0 - w_1x_1) \times (-1) \\= 2(w_0 + w_1x_1 - y_i) ∂w0∂S(yi−(w0+w1x1))2=2(yi−w0−w1x1)d(−w0)=2(yi−w0−w1x1)×(−1)=2(w0+w1x1−yi)
最小化 S, 将上面的偏导结果等于 0:
2 ∑ i = 1 n ( w 0 + w 1 x 1 − y i ) = 0 2\sum\limits_{i=1}^{n}(w_0 + w_1x_1 - y_i) = 0 2i=1∑n(w0+w1x1−yi)=0
线性回归的模型假设
线性关系
线性回归模型嘉定因变量和自变量之间存在线性关系 (Linear Relationship), 即两者之间的关系可以用过一个或多个系数 (w1, w2) 乘以预测变量 (x1, x2) 加上一个常数来表示 (w0). 这是线性回归模型的基础, 违反这个假设可能导致模型的预测能力下降.
线性关系是线性回归名称的起源. 如果这一假设不满足, 那么线性回归模型就不是一个合适的选择. 因为我们无法通过直线来准确的捕获因变量和自变量之间的关系.
如何判断是否为线性关系:
"""
@Module Name: 通过残差图判断线性关系.py
@Author: CSDN@我是小白呀
@Date: October 17, 2023
Description:
通过残差图判断线性关系
"""
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight") # 设置绘图样式
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体 'SimHei'
plt.rcParams['axes.unicode_minus']=False
# 设置随机数种子
np.random.seed(0)
# 模拟线性数据 y = 3x + b
X_linear = np.random.rand(100, 1) * 10 # 100个样本, 范围0-10
y_linear = 3 * X_linear + np.random.randn(100, 1) * 2 # 线性关系 + 噪声 (0-1)
# 模拟非线性数据 y = 3x^2 + b
X_non_linear = np.random.rand(100, 1) * 10 # 100个样本, 范围0-10
y_non_linear = 3 * X_non_linear**2 + np.random.randn(100, 1) * 2 # 二次方关系 + 噪声 (0-1)
# 实例化线性回归模型
model = LinearRegression()
# 训练线性
model.fit(X_linear, y_linear) # 训练
y_linear_pred = model.predict(X_linear) # 预测
residuals_linear = y_linear - y_linear_pred # 计算残差
# 训练非线性
model.fit(X_non_linear, y_non_linear) # 训练
y_non_linear_pred = model.predict(X_non_linear) # 预测
residuals_non_linear = y_non_linear - y_non_linear_pred # 计算残差
# 绘制残差图
f, ax = plt.subplots(1, 2, figsize=(16, 8))
f.suptitle('残差图')
# 线性残差图
sns.residplot(ax=ax[0], x=y_linear_pred.flatten(), y=residuals_linear.flatten(), lowess=True, line_kws={'color': 'red', 'lw': 1})
ax[0].axhline(y=0, color='gray', linestyle='--')
ax[0].set_xlabel('预测值')
ax[0].set_ylabel('残差')
ax[0].set_title('线性数据残差图')
# 非线性残差图
sns.residplot(ax=ax[1], x=y_non_linear_pred.flatten(), y=residuals_non_linear.flatten(), lowess=True, line_kws={'color': 'red', 'lw': 1})
ax[1].axhline(y=0, color='gray', linestyle='--')
ax[1].set_xlabel('预测值')
ax[1].set_ylabel('残差')
ax[1].set_title('非线性数据残差图')
plt.show()
输出结果:
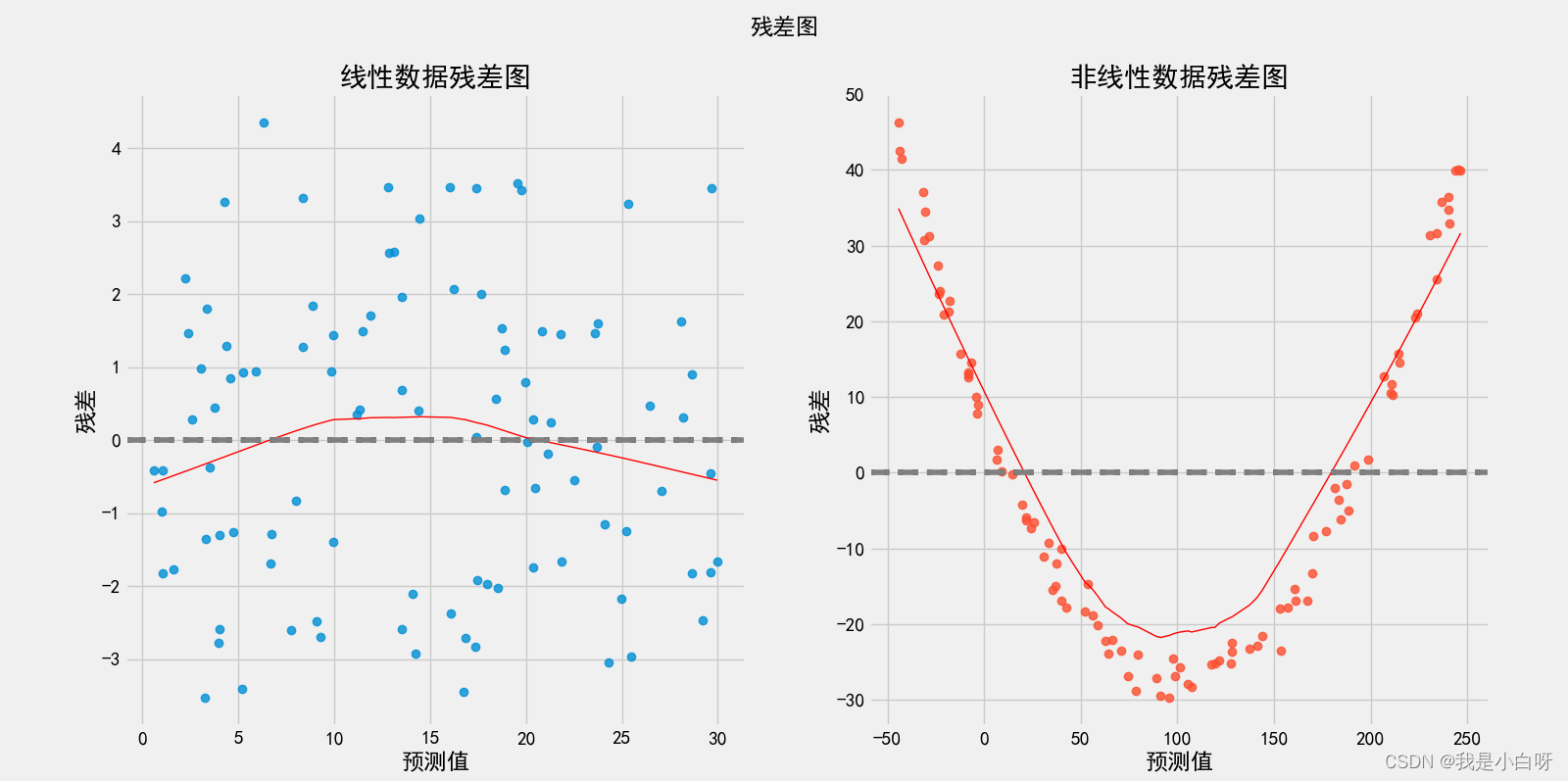
残差图 (Residual Plot) 是指以残差 (Residual), 目标值和预测值之差, 为纵坐标. 以任何其他指定的量为横坐标的散点图. 上述图片左边就是一个 0 均值的白噪音分布, 右图就存在残差值. 一个线性关系的残差图, 不应该包含任何可预测信息.
独立性
误差项应该是独立的, 这意味着每个数据的误差与其他数据的误差不相关. 如果误差不是独立的, 那么模型可能会缺乏一定的信息, 导致预测偏差.
如何判断独立性:
Durbin-Watson 检测是一个常用方法, 用于检测连续观测值误差的连续性. Durbin-Watson 值的范围为 0~4, 小于 1.5 代表正自相关性, 大于 1.5 表示负自相关性, 1.5-2.5 之间说明不存在自相关.
判断独立性:
"""
@Module Name: 通过残差图判断独立性.py
@Author: CSDN@我是小白呀
@Date: October 17, 2023
Description:
通过残差图判断独立性
"""
import numpy as np
import statsmodels.api as sm
from statsmodels.regression.linear_model import OLS
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight") # 设置绘图样式
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体 'SimHei'
plt.rcParams['axes.unicode_minus']=False
# 设置随机数种子
np.random.seed(0)
# 独立残差数据
X = np.random.rand(100, 1) * 10 # 100个样本, 范围0-10
y = 3 * X + np.random.randn(100, 1) * 2 # 线性关系 + 噪声 (0-1)
# 残差正相关数据
X_positive = np.arange(100)
y_positive = np.array([1 for _ in range(100)])
# 正相关数据残差
model = OLS(y, X).fit() # 使用 statsmodels 进行线性回归
residuals = model.resid # 获取残差
# 独立数据残差
model = OLS(y_positive, X_positive).fit() # 使用 statsmodels 进行线性回归
residuals_positive = model.resid # 获取残差
# 进行Durbin-Watson测试
dw = sm.stats.durbin_watson(residuals)
dw_positive = sm.stats.durbin_watson(residuals_positive)
# 调试输出
print("独立残差数据 Durbin-Watson值:", dw)
print("正自相关残差数据 Durbin-Watson值:", dw_positive)
# 绘制残差图
f, ax = plt.subplots(1, 2, figsize=(16, 8))
f.suptitle('Durbin-Watson 自相关性 (独立性)')
# 线性残差图
sns.scatterplot(ax=ax[0], x=[i for i in range(100)], y=residuals)
ax[0].axhline(y=0, color='gray', linestyle='--')
ax[0].set_ylabel('残差')
ax[0].set_title('无自相关性')
# 非线性残差图
sns.scatterplot(ax=ax[1], x=[i for i in range(100)], y=residuals_positive)
ax[1].axhline(y=0, color='gray', linestyle='--')
ax[1].set_ylabel('残差')
ax[1].set_title('正自相关性')
plt.show()
输出结果:
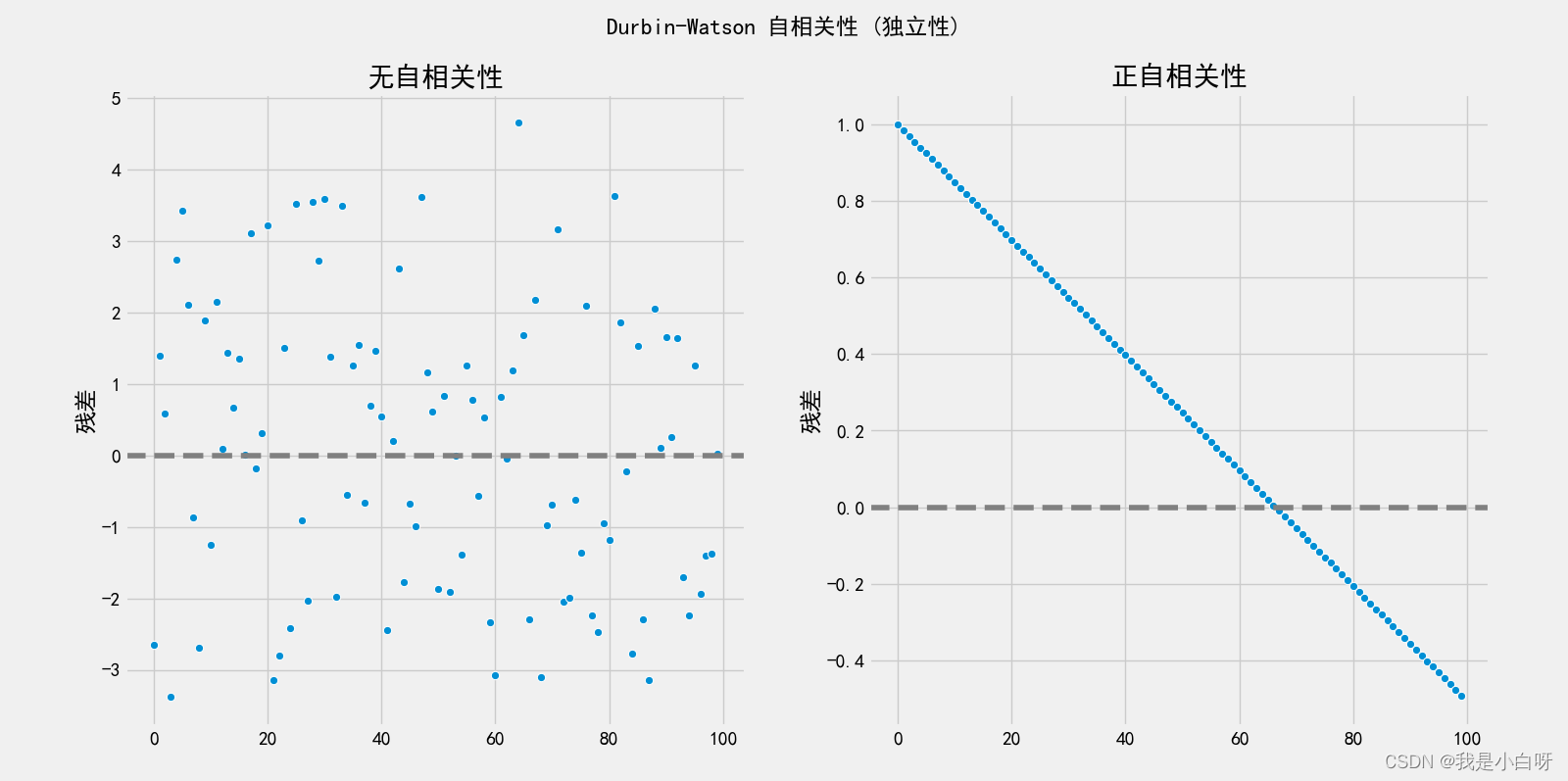
独立残差数据 Durbin-Watson值: 2.100345841035149
正自相关残差数据 Durbin-Watson值: 0.0008866112741927459
注: 正自相关性 (Positive Autocorrelation) 指的是数据呈现一个明确的线性递增或递减趋势, 即每个数据和前后数据高度相关, 而不是随机噪声. 左图属于随机噪声, 无自相关性, Durbin-Watson 值在 1.5-2.5 之间, 右图呈现高度正自相关性.
同方差性
同方差性 (Homoscedasticity) 指的是无论预测变量的值如何, 模型的同方差都应该保持恒定. 同方差性为回归分析提供了稳定性和效率, 当不满足同方差性时, 回归模型可能会偏向于某些观测值, 从而影响模型的整体预测效果. 而且如果存在异方差性

残差是验证同方差性的常用工具, 通过绘制残差图, 我们可以检查分布是否均匀. 如果残差图中的点沿着 0 线随机分布, 则同方差成立, 反义如果图中的点呈现出某种模式, 例如随着预测值的增加而扩散, 那么就是异方差性 (Heteroscedasticity). 上述图片左边的图就属于同方差性, 右边就属于异方差性.
正态分布误差
正态分布误差 (Normality of Error) 指的是线性回归中模型的误差或残差应符合正态分布.
例子:
"""
@Module Name: 通过残差图判断正态分布.py
@Author: CSDN@我是小白呀
@Date: October 17, 2023
Description:
通过残差图判断正态分布
"""
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight") # 设置绘图样式
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体 'SimHei'
plt.rcParams['axes.unicode_minus']=False
# 设置随机数种子
np.random.seed(0)
# 模拟线性数据 y = 3x + b
X_linear = np.random.rand(1000, 1) * 10 # 1000个样本, 范围0-10
y_linear = 3 * X_linear + np.random.randn(1000, 1) * 2 # 线性关系 + 噪声 (0-1)
# 模拟非线性数据 y = 3x^2 + b
X_non_linear = np.random.rand(1000, 1) * 10 # 1000个样本, 范围0-10
y_non_linear = 3 * X_non_linear**2 + np.random.randn(1000, 1) * 2 # 二次方关系 + 噪声 (0-1)
# 实例化线性回归模型
model = LinearRegression()
# 训练线性
model.fit(X_linear, y_linear) # 训练
y_linear_pred = model.predict(X_linear) # 预测
residuals_linear = y_linear - y_linear_pred # 计算残差
# 训练非线性
model.fit(X_non_linear, y_non_linear) # 训练
y_non_linear_pred = model.predict(X_non_linear) # 预测
residuals_non_linear = y_non_linear - y_non_linear_pred # 计算残差
# 绘制残差图
f, ax = plt.subplots(1, 2, figsize=(16, 8))
f.suptitle('正态分布')
# 最大残差
print("线性残差范围:", residuals_linear.min(), "-", residuals_linear.max())
print("非线性残差范围:", residuals_non_linear.min(), "-", residuals_non_linear.max())
# 线性残差图
sns.histplot(ax=ax[0], data=residuals_linear.flatten(), bins=20)
ax[0].set_xlabel('残差值')
ax[0].set_ylabel('数量')
ax[0].set_title('线性数据正态分布图')
# 非线性残差图
sns.histplot(ax=ax[1], data=residuals_non_linear.flatten(), bins=20)
ax[1].set_xlabel('残差值')
ax[1].set_ylabel('数量')
ax[1].set_title('非线性数据正态分布图')
plt.show()
输出结果:
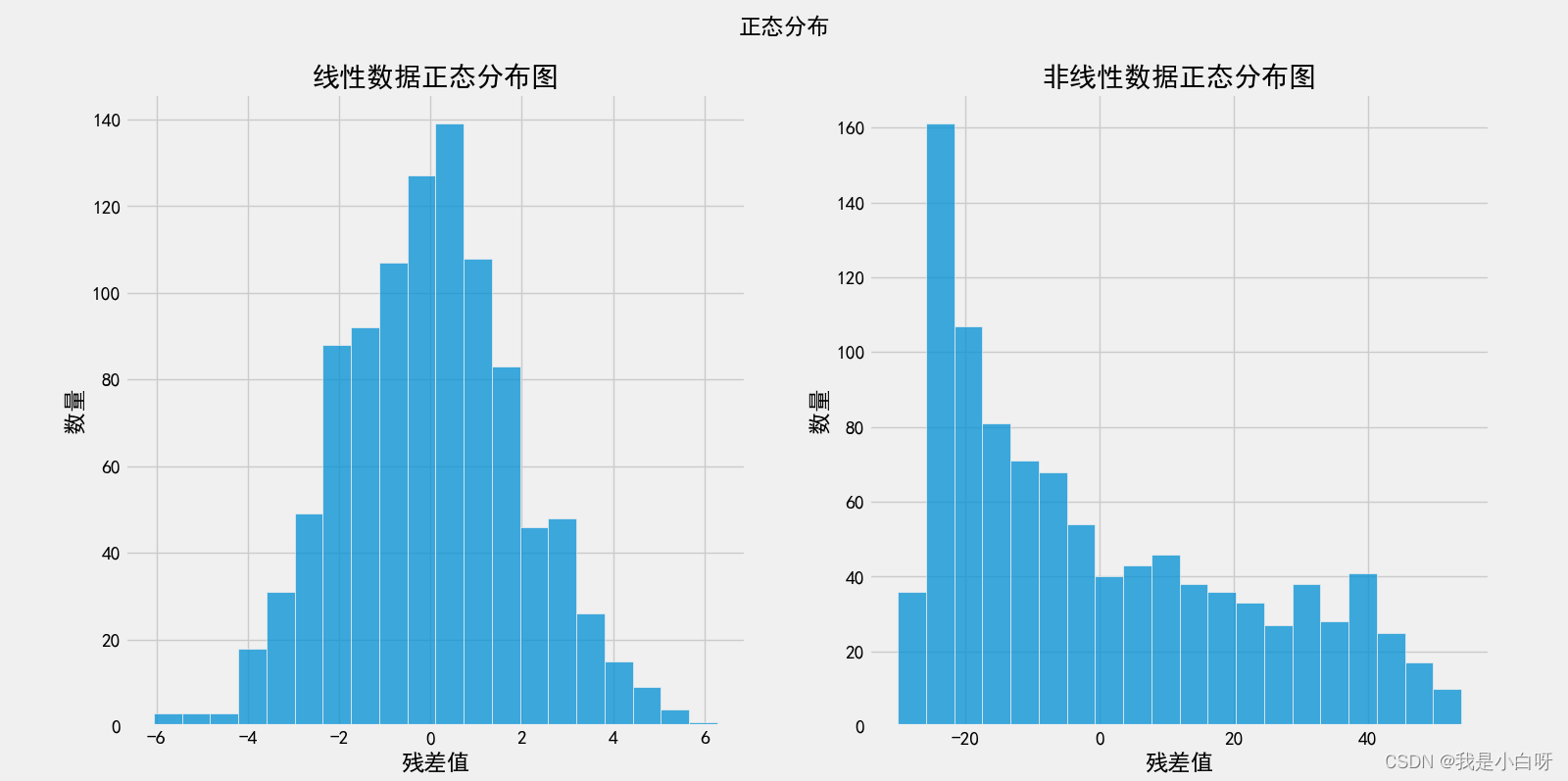
线性残差范围: -6.064887209285082 - 6.284146438819695
非线性残差范围: -30.07255606488623 - 53.966957811451316
我们可以看到符合线性关系的数据残差符合正态分布, 而非线性的不符合.
梯度下降
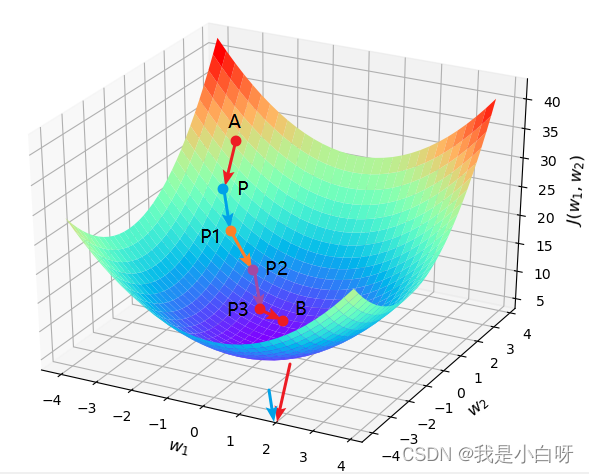
梯度下降 (Gradient Descent) 是一个用于优化函数的迭代方法. 在机器学习 (Machine Learning) 和深度学习 (Deep Learning) 中, 我们常用梯度下降来最小化 (最大化) 损失函数, 进而找到模型的最优参数.
工作原理
梯度下降的核心思想很简单: 找到损失函数的斜率 (梯度), 然后沿着斜率的反方向更新模型的参数, 逐步减小损失.
梯度下降的公式
公式:
w n e x t = w − l r × ∂ l o s s ∂ w w_{next} = w - lr\times \frac{\partial loss}{\partial w} wnext=w−lr×∂w∂loss
- w n e x t w_{next} wnext: 是梯度下降过程中的下一个权重
- lr: Learning Rate 学习率
- ∂ l o s s ∂ w \frac{\partial loss}{\partial w} ∂w∂loss: 误差函数的导数
下面我们来推导一下:
我们已知: M S E = 1 n ∑ i = 1 n ( y i − y ˆ i ) 2 y = w 0 + w 1 x 1 MSE = \frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \^y_i)^2\\y = w_0 + w_1x_1 MSE=n1i=1∑n(yi−yˆi)2y=w0+w1x1
在梯度下降中, 我们的目标是调整模型参数 (权重和偏置, w 和 b 或 w0) 以最小化损失函数, 所以我们需要对模型参数 (w 和 w0) 求偏导:
w1 (权重) 求导:
∂ M S E ∂ w 1 = 1 n ∑ i = 1 n ( w 0 + w 1 x 1 ) 2 d w = 2 n ∑ i = 1 n x ( w 0 + w 1 x 1 ) \frac{\partial MSE}{\partial w_1} = \frac{1}{n}\sum\limits_{i=1}^{n}(w_0 + w_1x_1)^2dw \\=\frac{2}{n}\sum\limits_{i=1}^{n}x(w_0 + w_1x_1) ∂w1∂MSE=n1i=1∑n(w0+w1x1)2dw=n2i=1∑nx(w0+w1x1)
w0 (偏置) 求导:
∂ M S E ∂ w 0 = 1 n ∑ i = 1 n ( w 0 + w 1 x 1 ) 2 d w = 2 n ∑ i = 1 n ( w 0 + w 1 x 1 ) \frac{\partial MSE}{\partial w_0} = \frac{1}{n}\sum\limits_{i=1}^{n}(w_0 + w_1x_1)^2dw \\=\frac{2}{n}\sum\limits_{i=1}^{n}(w_0 + w_1x_1) ∂w0∂MSE=n1i=1∑n(w0+w1x1)2dw=n2i=1∑n(w0+w1x1)
如果有 w2, w3 以此类推, 这边我就不写了.
计算新的权重, 将上面的导数代入梯度下降公式, 我们可以得到:
w 1 n e x t = w 1 − l r × ∂ l o s s ∂ w 1 = w 1 − l r × 2 n ∑ i = 1 n x ( w 0 + w 1 x 1 ) w_{1next} = w_1 - lr\times \frac{\partial loss}{\partial w_1} \\=w_1 - lr\times\frac{2}{n}\sum\limits_{i=1}^{n}x(w_0 + w_1x_1) w1next=w1−lr×∂w1∂loss=w1−lr×n2i=1∑nx(w0+w1x1)
同理:
w 0 n e x t = w 0 − l r × ∂ l o s s ∂ w 0 = w 1 − l r × 2 n ∑ i = 1 n ( w 0 + w 1 x 1 ) w_{0next} = w_0 - lr\times \frac{\partial loss}{\partial w_0} \\=w_1 - lr\times\frac{2}{n}\sum\limits_{i=1}^{n}(w_0 + w_1x_1) w0next=w0−lr×∂w0∂loss=w1−lr×n2i=1∑n(w0+w1x1)
在代码中:
# 计算w的导, w的导 = 2x(wx+b-y)
w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)
# 计算b的导, b的导 = 2(wx+b-y)
b_gradient += (2 / N) * ((w_current * x + b_current) - y)
梯度下降的变种
- 批量梯度下降 (BGD, Batch Gradient Descent): 每次使用这个训练集来计算梯度
- 随机梯度下降 (SGD, Stochastic Gradient Descent): 每次只使用一个样本来计算梯度
- 小批量梯度下降 (Mini-Batch Gradient Descent): 使用一个小批量的样本来计算梯度
学习率
寻找山谷的最低点, 也就是我们的目标函数终点 (什么样的参数能使得目标函数达到极值点)
下山分几步走呢?
- 找到当前最合适的方向
- 走一小步
- 按照方向与步伐去更新我们的参数
学习率 (learning_rate): 对结果影响较大, 越小越好.
数据批次 (batch_size): 优先考虑内存和效率, 批次大小是次要的.
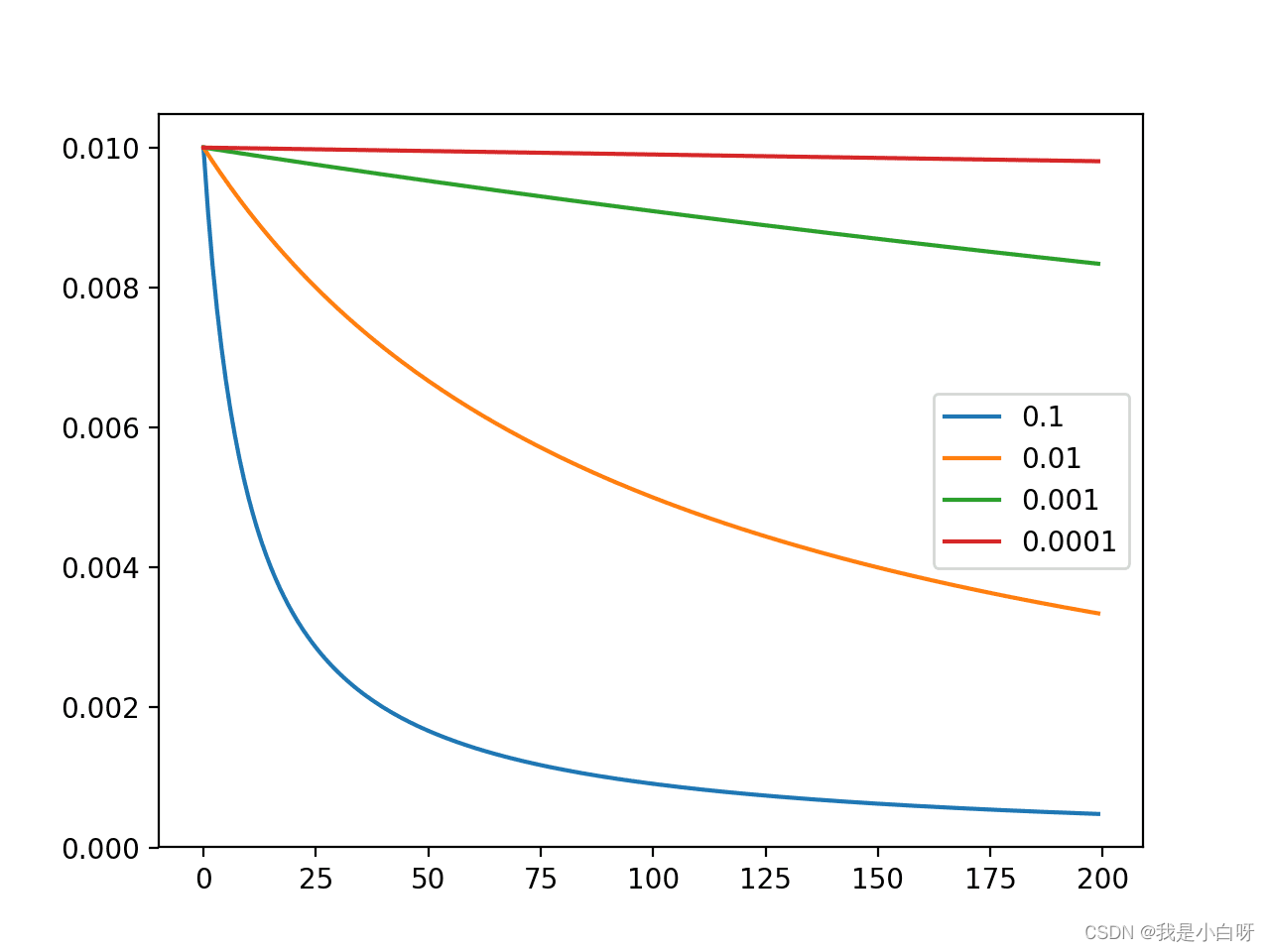
选择适当的学习率非常重要:
- 太小的学习率: 收敛速度慢
- 太大的学习率: 会错过最小值, 或梯度爆炸
常见的操作有:
- 学习率衰减或学习率退火 (Learning Rate Decay 或 Cosine Annealing), 即学习率随着迭代次数逐渐减小
线性回归实现波士顿放假预测
"""
@Module Name: 线性回归预测波士顿房价.py
@Author: CSDN@我是小白呀
@Date: October 17, 2023
Description:
线性回归预测波士顿房价
"""
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 加载数据集
boston_data = load_boston()
X = boston_data.data
y = boston_data.target
# 调试输出数据基本信息
print("输出特征:", X[:5])
print("输出标签:", y[:5])
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 实例化模型
lin_reg = LinearRegression()
# 训练模型
lin_reg.fit(X_train, y_train)
# 预测
y_pred = lin_reg.predict(X_test)
# 模型评估
MSE = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("Mean Squared Error (MSE):", MSE)
print("R^2 Score:", r2)
输出结果:
输出特征: [[6.3200e-03 1.8000e+01 2.3100e+00 0.0000e+00 5.3800e-01 6.5750e+00
6.5200e+01 4.0900e+00 1.0000e+00 2.9600e+02 1.5300e+01 3.9690e+02
4.9800e+00]
[2.7310e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 6.4210e+00
7.8900e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9690e+02
9.1400e+00]
[2.7290e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 7.1850e+00
6.1100e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9283e+02
4.0300e+00]
[3.2370e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 6.9980e+00
4.5800e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9463e+02
2.9400e+00]
[6.9050e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 7.1470e+00
5.4200e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9690e+02
5.3300e+00]]
输出标签: [24. 21.6 34.7 33.4 36.2]
Mean Squared Error (MSE): 33.4489799976764
R^2 Score: 0.5892223849182523
手搓线性回归
为了大家更好的理解, 我们最后带领大家在不使用任何包的情况下实现线性回归.
代码:
"""
@Module Name: 手把手实现线性回归.py
@Author: CSDN@我是小白呀
@Date: October 17, 2023
Description:
手把手实现线性回归算法
"""
class LinearRegression:
def __init__(self, learning_rate=0.000003, num_iterations=100000):
"""
初始化线性回归模型
:param learning_rate: 学习率
:param num_iterations: 迭代次数
"""
self.learning_rate = learning_rate
self.num_iterations = num_iterations
self.weights = None # 权重w
self.bias = None # 偏置b
def fit(self, X, y):
"""
训练模型
:param X: 训练特征
:param y: 训练标签
:return:
"""
num_samples, num_features = X.shape
self.weights = [0] * num_features
self.bias = 0
# 梯度下降
for _ in range(self.num_iterations):
model_output = self._predict(X)
# 计算梯度
# 计算w的导, w的导 = 2x(wx+b-y)
d_weights = (-2/num_samples) * X.T.dot(y - model_output)
# 计算b的导, b的导 = 2(wx+b-y)
d_bias = (-2/num_samples) * sum(y - model_output)
# 更新梯度
self.weights -= self.learning_rate * d_weights
self.bias -= self.learning_rate * d_bias
def predict(self, X):
return self._predict(X)
def _predict(self, X):
return X.dot(self.weights) + self.bias
if __name__ == '__main__':
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# 加载数据集
boston_data = load_boston()
X = boston_data.data
y = boston_data.target
# 查看nan
# print(pd.DataFrame(X).isnull().sum())
# 调试输出数据基本信息
print("输出特征:", X[:5])
print("输出标签:", y[:5])
# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 实例化模型
lin_reg = LinearRegression()
# 训练模型
lin_reg.fit(X_train, y_train)
# 预测
y_pred = lin_reg.predict(X_test)
# 模型评估
MSE = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("Mean Squared Error (MSE):", MSE)
print("R^2 Score:", r2)
输出结果:
输出特征: [[6.3200e-03 1.8000e+01 2.3100e+00 0.0000e+00 5.3800e-01 6.5750e+00
6.5200e+01 4.0900e+00 1.0000e+00 2.9600e+02 1.5300e+01 3.9690e+02
4.9800e+00]
[2.7310e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 6.4210e+00
7.8900e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9690e+02
9.1400e+00]
[2.7290e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 7.1850e+00
6.1100e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9283e+02
4.0300e+00]
[3.2370e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 6.9980e+00
4.5800e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9463e+02
2.9400e+00]
[6.9050e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 7.1470e+00
5.4200e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9690e+02
5.3300e+00]]
输出标签: [24. 21.6 34.7 33.4 36.2]
Mean Squared Error (MSE): 43.28945498976922
R^2 Score: 0.46837424997350163