网络群体与市场的一个课程小作业,整理一下发出来~ 本人目前还处于学习的初级阶段,有问题请多多指教~
一、课堂内容
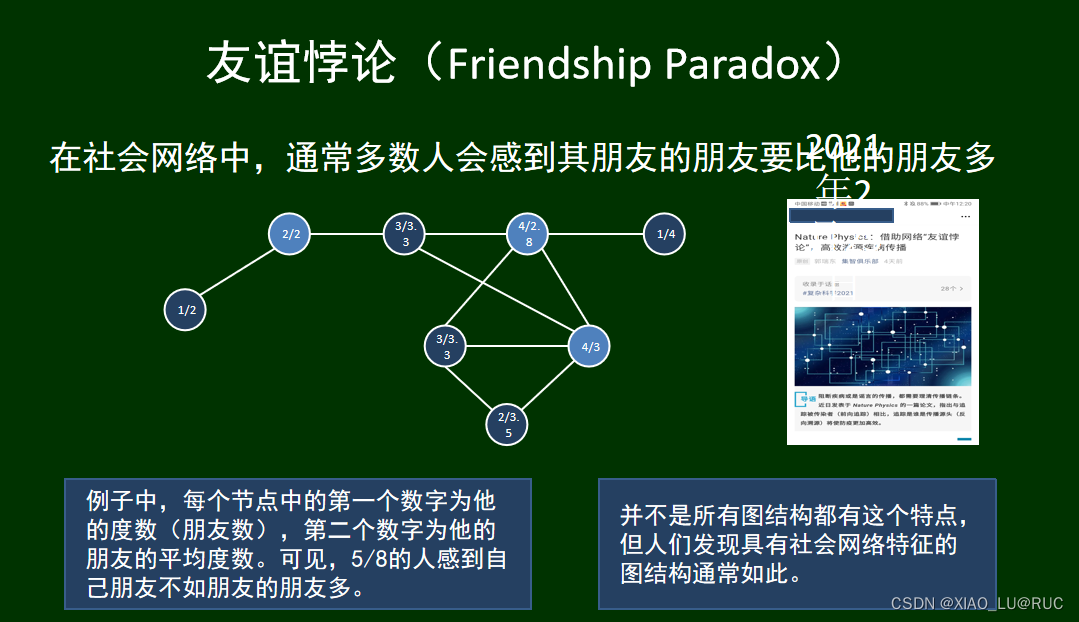
(来自Dou老师课堂的PPT)
二、实验目的重述
友谊悖论,指多数人一般似乎都感到朋友的朋友多于自己的朋友。一种解释是人们倾向于和比较活跃的人交友。在网络(无向图)G(V,E) 中,表达为多数节点的度数通常小于它邻居节点的平均度数,即

友谊悖论并不是在每个网络中都会出现。本实验随机生成一些符合社会网络特征的网络(以邻接矩阵方式表示),通过计算其中友谊悖论出现的占比,分析友谊悖论是否是一个规律。
三、思路分析
为了探究友谊悖论的普遍规律性,本实验应用社交网络中满足友谊悖论的节点占总节点数的比率来探究悖论是否具有规律性,若这一比率(以下简称为”悖论比率“)较大(大于50%,意味着不是随机现象,若70%-100%,则规律性较强),则可以说明友谊悖论具有一定规律性。同时,应考虑不同社交网络规模下,这一悖论的实际情况。
首先,本实验通过随机生成不同维邻接矩阵实现无向图,用来模拟现实中的社交网络的情况。针对每一维情况下的邻接矩阵,实验生成20个不同随机矩阵,分析这20个无向图的悖论比率,求平均值作为这一维度下社交网络的悖论比率。
其次,对于每一随机生成的无向图,判断其各个节点是否满足友谊悖论。具体方法为:遍历每一节点,得到这一节点的邻居节点,再将这些邻居节点的度数求平均值,得到这一节点的所有邻居节点的平均朋友数,将这个数与节点邻居数相比,得到该点是否符合友谊悖论。建立一个参数记录当前无向图下,满足友谊悖论的节点总数。用悖论节点数/节点总数得到悖论比率。
最后将不同维度的邻接矩阵(无向图)的悖论比率记录为列表,输出分析图像。
四、代码实现
1. 引入需要的库
import numpy as np
import matplotlib.pyplot as plt2. 随机生成n维邻接矩阵模拟无向图网络
# 随机生成邻接矩阵
def generate_random_adjacency_matrix(n):
if n <= 0:
return None
# 生成一个n x n的零矩阵
adjacency_matrix = np.zeros((n, n), dtype=int)
# 随机填充矩阵,确保对称性(无向图)
for i in range(n):
for j in range(i+1, n):
# 生成随机的0或1表示连接或不连接
value = np.random.randint(0, 2)
adjacency_matrix[i, j] = value
adjacency_matrix[j, i] = value
# print(adjacency_matrix)
return adjacency_matrix模拟矩阵结果样例——满足对称性(这是两个不同的随机生成的矩阵)

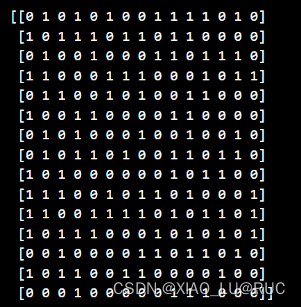
3. 判断节点是否满足友谊悖论
获取节点的相邻节点,并计算相邻节点度数之和,除以相邻节点个数得到当前节点的平均朋友数。以下是是样例详细计算过程:
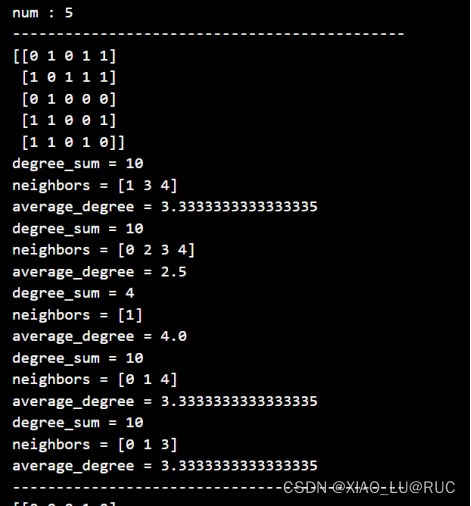
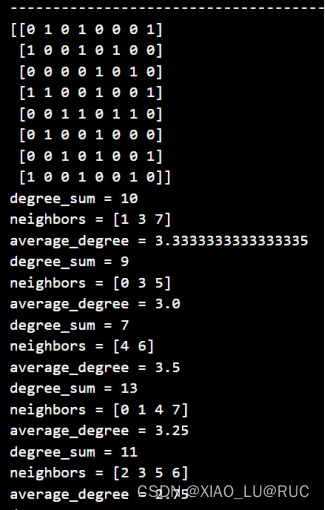
代码实现:
# node_index为指定节点
# 是否符合友谊悖论的判断函数
def average_degree_of_node(adjacency_matrix, node_index,n):
if node_index < 0 or node_index >= len(adjacency_matrix):
return None
# 获取节点的相邻节点
neighbors = np.where(adjacency_matrix[node_index] == 1)[0]
# print(neighbors)
if len(neighbors) == 0:
return 0 # 如果节点没有相邻节点,平均度数为0
# 计算相邻节点的度数之和
degree_sum = 0
for i in neighbors:
degree_sum += np.sum(adjacency_matrix[i])
# print(f"degree_sum = {degree_sum}")
# print(f"neighbors = {neighbors}")
# 计算平均度数
average_degree = degree_sum / len(neighbors)
# print(f"average_degree = {average_degree}")
# 比较是否符合友谊悖论
# 如果相邻节点平均度数小于等于自身度数,则不符合友谊悖论
if average_degree < len(neighbors):
return 0
# 如果相邻节点平均度数大于等于自身度数,则符合友谊悖论
else:
return 13. 主函数
# 主函数
def main():
num_ratio_average = []
num_list = []
for num in range(1000,2000,250):
print(f"num : {num}")
# 横坐标是num维矩阵,升序
num_list.append(num)
# 新建list_ratio存放每个随机邻接矩阵的符合友谊悖论结点的占比
list_ratio = []
# 生成20个结点数为n的邻接矩阵
for i in range(0,5):
# print("---------------------------------------------")
# n = 15
this_matrix = generate_random_adjacency_matrix(num) # 此处n = 15
# print(this_matrix)
fit = 0
# 对于每一个结点
for index in range(0,num):
# 判断当前结点是否符合友谊悖论
# 如果符合, fit计数+1
if average_degree_of_node(this_matrix, index,num) == 1:
fit += 1
# print(f"Ratio in each matrix:{fit/n}")
list_ratio.append(fit/num)
# 计算每num维的矩阵下,平均的悖论ratio
average = sum(list_ratio) / len(list_ratio)
num_ratio_average.append(average)
print(num_ratio_average)
print(num_list) 4. 绘制悖论比例与矩阵维度(朋友节点个数)的关系图像
plt.plot(num_list, num_ratio_average, marker='o', linestyle='-')
plt.title('Certification of Friendship Paradox')
plt.xlabel('Number of Friends')
plt.ylabel('Ratio of Paradox')
# 显示图形
plt.show() 5. 运行主函数
if __name__ == "__main__":
# 当脚本直接运行时,将执行主函数
main()
五、实验结果分析
| 矩阵维度 |
4 |
54 |
104 |
154 |
204 |
254 |
304 |
354 |
404 |
454 |
| Ratio |
0.648 |
0.578 |
0.539 |
0.524 |
0.521 |
0.520 |
0.515 |
0.525 |
0.517 |
0.516 |
| 矩阵维度 |
504 |
554 |
604 |
654 |
704 |
754 |
804 |
854 |
904 |
954 |
| Ratio |
0.515 |
0.515 |
0.519 |
0.515 |
0.513 |
0.509 |
0.517 |
0.514 |
0.514 |
0.511 |

运行过程中,记录随机生成邻接矩阵的维度和图中满足友谊悖论的结点比率,绘制成图像。当图中的结点总数较少时,满足友谊悖论结点的比例较高,可以判断结点数小于50时,满足友谊悖论结点的比率约在60%。而这一现象随着结点数增加、社交网络的扩大而减少:随着结点数增加至1000+,满足友谊悖论结点比率逐渐减少并收敛至约51%。由此推断,当社交网络扩大至一定规模时,友谊悖论的满足比约在50%。

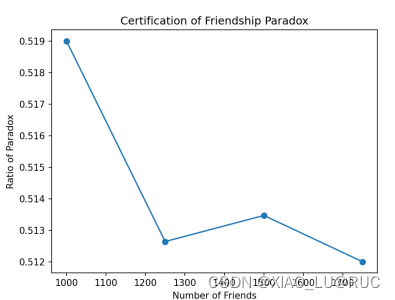
(图像横坐标为社交网络中节点数,纵轴为悖论节点比率)
因此,作者认为,当分析的社交网络范围较小时,可以说友谊悖论是一个规律,而当分析的社交网络范围较大时,由于这种现象出现的概率约为50%,因此可能是一种随机现象,而并非一个规律。