理解Bellman-Ford算法

Bellman-Ford算法（下文中简称为BF）与Dijkstra算法一样，解决的是单源最短路径问题。两者不同之处在于，后者只适用于无负权边的图，而BF无此限制：只要图中没有负权环，则该算法可以正确地给出起点到其余各点的最短路径，否则报告负权环的存在。

很多资料（比如维基百科）在解释BF时都会提到它的基础或者核心是松弛操作。自然地，理解BF的关键也是理解这一点，所以下面就来专门讲讲它究竟是个什么意思。

“松弛”，翻译自英文的relaxation，原本指数学上的一种迭代求解方程组的方法，表示通过改进近似解来不断地逼近最终解或者说最优解的方法。而我们下面可以看到，BF正是这么一个迭代改进的过程。

岔开一笔，我不知道当初数学家们为什么要选用relaxation这个词，但我觉得它的字面意义正好与它所代表的实际过程相反（在BF中尤其如此）。更糟的是，数学中另有一个“松弛”的概念，使用的是同一个词。它表示的是一种解决问题的技巧：如果问题难以解决，则放宽某些限制，将其转化成容易解决的问题，以求得近似的解决方案（这倒是名副其实）。所以，在理解BF时，看到“松弛”这个词，如果觉得它有误导之嫌，不妨在脑中将其替换为“逼近”或者“改进”。

那么BF中的松弛改进是个怎么样的操作呢？

首先，松弛改进的对象很明显，就是从起点到其余各点的距离。给定图G和起点s，G[u][v]表示边(u, v)的长度，且用D[u]表示从s点到u点已知的（但不一定是最优的）最短路径的长度，那么对于图中任何一条边(u, v)，如果D[u] + G[u][v]小于D[v]，则将D[v]松弛改进为D[u] + G[u][v]。我们可以用Python给出下面的实现（代码出自Python Algorithms一书，稍有改动，下同）：

inf = float('inf')

def relax(G, u, v, D, P):
    old = D.get(v, inf) # 若D[v]不存在则返回inf
    new = D.get(u, inf) + G[u][v]
    if new < old:
        D[v], P[v] = new, u
        return True # 若有改进，则返回True

其次，根据定义，它肯定是一个迭代的过程。照上面的分析和代码，我们可以将每次松弛改进和某条边对应起来。讲到这里，那么BF的核心思想其实就很容易描述了：不断地选择一条边，做松弛改进操作，直到得出正确的解答。

接下来的问题自然就是：1. 这种思路能提供一个正确的算法吗？换言之，我们如何通过选择松弛改进边的顺序，使得对应的BF最终完成运行？2. 如何选择松弛改进边的顺序，使得对应的BF效率最高？

我们先来考察如下的情况：如果对图里每条边按照随机的顺序都做一次松弛改进（称之为一轮松弛改进），能得到什么？能够保证起点s的任一邻点（记作u）都得到正确的D[u]（最短路径长度）和P[u]（最短路径中的上一节点）吗？显然不能，因为松弛改进的最优顺序是无法预先知晓的。比如下图中，如果顺序是(s, a)、(s, b)、(s, c)、(a, b)、(b, c)，那么一轮下来，确实a点b点c点都能得到正确答案。但如果顺序变成(b, c)、(a, b)、(s, a)、(s, b)、(s, c)，那么b点的答案就是错的（读者可自行推演验证）。

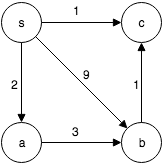
怎么去找这么个最优的顺序呢？这样的话，只需一轮松弛改进就可以解决问题了。其实这是不现实的。因为要得到这个最优顺序，从本质上来讲，必须得将各点以距起点s的最短距离从小到大作一个排序，而这正就是要解决的问题。这是个循环，没有出路。

回到上图完成一轮松弛改进之时。可以发现，虽然b点的答案不一定正确，但是a点和c点的答案，不论顺序如何，都是正确的。这是一个非常关键的性质。换句话说，完成第1轮松弛改进后，对于任一节点u，如果s到u存在一条边数（注意不是长度）为1的最短路径，那么从s到u点的（某条）边数为1最短路径的就一定能解出来。推而广之，如果连做k轮松弛改进，对于任一节点u，如果从s到u存在边数为k的、且没有边数更少的最短路径，那是不是也能把其中一条给解出来呢？是的。我们可以用数学归纳法进行证明。假设k-1轮后的情况已经得证，再假设s到某个点u存在边数为k的最短路径，且其中一条为[s, m1, m2, ..., mk-2, u]，那么，[s, m1, m2, ..., mk-2]肯定是从s到mk-2的一条最短路径（可用反证法证明），进而在第k轮处理(mk-2, u)的时候，一定会对D[u]和P[u]的值有所改进（也就是说relax方法返回True），两者的值都会是最终正确的解答而且不会再发生改变了。综上，前面的命题得证。

另外，还有一个特别重要的引理：如果一个节点数为n的图中没有负权环，那么其任意两个节点之间一定存在最短路径，且其边数不会超过n-1。这一引理从直观上很好理解，所以这里不给出严谨的数学证明。这条引理非常重要，因为它有两个很关键的推论：

在无负权环、节点数为n的图中，遵循上面的思路，我们最多只需要进行n-1轮松弛改进，就可以解决单源最短路径问题
对于节点数为n的图，如果如上进行n轮松弛改进，且最后一轮还能够有所改进，则说明图中必有负权环

以上就是BF的整个思路。依此可以用Python做出如下代码实现：

def bellman_ford(G, s):
    D, P = {s: 0}, {s: None}
    for _ in G: # 轮数等于节点数
        improved = False
        for u in G:
            for v in G[u]:
                if relax(G, u, v, D, P):
                    improved = True
        if not improved: # 如果某轮没有任何改进
            break        # 说明问题已经解决，退出循环
    else:                # 否则，说明第n轮也有改进，存在负权环
        raise ValueError('negative cycle')
    return D, P

很显然，上面算法的时间复杂度为O(nm)，其中n和m分别为节点和边的数目。相比起Dijkstra算法的O(mlgn)，这不算是很快的算法，但BF的优势，正如一开始所说的，在于它允许负权边的存在而且能够检测到负权环的存在。

理解Bellman-Ford算法

猜你喜欢