1. 核函数Kernel
1.1 特征空间的隐式映射:核函数
事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
具体来说,在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。如图7-7所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
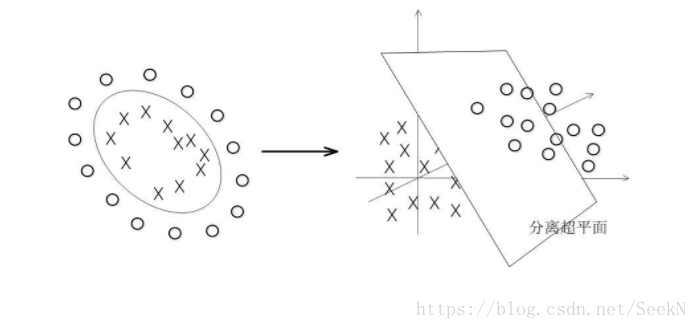
而在我们遇到核函数之前,如果用原始的方法,那么在用线性学习器学习一个非线性关系,需要选择一个非线性特征集,并且将数据写成新的表达形式,这等价于应用一个固定的非线性映射,将数据映射到特征空间,在特征空间中使用线性学习器,因此,考虑的假设集是这种类型的函数:
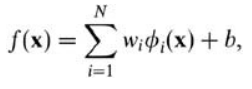
这里ϕ:X->F是从输入空间到某个特征空间的映射,这意味着建立非线性学习器分为两步:
1.首先使用一个非线性映射将数据变换到一个特征空间F,
2.然后在特征空间使用线性学习器分类。
而由于对偶形式就是线性学习器的一个重要性质,这意味着假设可以表达为训练点的线性组合,因此决策规则可以用测试点和训练点的内积来表示:
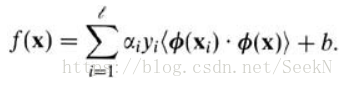
如果有一种方式可以在特征空间中直接计算内积〈φ(xi · φ(x)〉,就像在原始输入点的函数中一样,就有可能将两个步骤融合到一起建立一个非线性的学习器,这样直接计算法的方法称为核函数方法:
核是一个函数K,对所有x,z(-X,满足
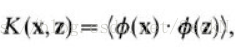
这里φ是从X到内积特征空间F的映射。
那么直接进行映射和用核函数有什么区别呢?
1. 一个是映射到高维空间中,然后再根据内积的公式进行计算;
2. 而另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射后的结果。
1.2 核函数的本质
上面说了这么一大堆,读者可能还是没明白核函数到底是个什么东西?我再简要概括下,即以下三点:
1. 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去;
2. 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的(要是19维(打个比方)乃至无穷维的例子)。那咋办呢?
3. 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。