转载请注明出处https://blog.csdn.net/bestsort
线段树是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&单点查询&&区间求和&&区间修改.
另外一个拥有类似功能的是树状数组,但是树状数组最常用的是单点修改&&区间求和.
线段树完全涵盖树状数组所有功能
具体区别和联系如下:
1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
说了这么多,其实线段树就是个二叉树而已,只不过叶子节点记录的是区间之间的和而已
先给一份样图
其中,矩形内的是区间之和,区间外的是数组下标(线段树用数组存数据).不难看出,线段树的左孩子=根节点下标*2,右孩子=根节点下标*2+1,而左右孩子则是根节点将区间二分的结果.
先给出线段树的结构体定义然后咱们再仔细讲讲各种(sao)操作
struct node {
int l,r,w,flag;
} a[maxn<<2]; //4倍空间
结构体里有个延迟标记的东西,咱们下面再说这个问题
需要注意的是如果是n个数,那么线段树需要开4n的空间.理论上是2n-1的空间,但是你递归建立的时候当前节点为r,那么左右孩子分别是2*r,2*r+1,此时编译器并不知道递归已结束,因为你的结束条件是在递归之前的,所以编译器会认为下标访问出错,也就是空间开小了,应该再开大2倍。有时候可能你发现开2,3倍的空间也可以AC,那只是因为测试数据并没有那么大。
至于为什么开4倍,我从网上摘抄了一部分(反正我是看不懂
首先线段树是一棵二叉树,最底层有n个叶子节点(n为区间大小)
那么由此可知,此二叉树的高度为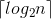
然后通过等比数列求和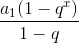
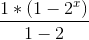
化简可得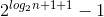
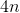
证毕
线段树的基础操作主要有5个:
建树、单点查询、单点修改、区间查询、区间修改。
----------------------------------------------------------------------------------
建树:会建二叉树的话这一条也就没什么说的了
主要就是递归建树而已
其中,k为根节点,l,r分别为左右区间
输入n个数将其建立为线段树只需要调用
build(1,1,n)即可
递归过程应该都能看懂(看不懂回去学二叉树去
void build(int k,int l,int r) {
a[k].l = l,a[k].r = r;
if(a[k].l == a[k].r) {
scanf("%d",&a[k].w);
//cin >> a[k].w;
return;
}
build(k*2,l,(l+r)/2); //左
build(k*2+1,(l+r)/2+1, r);//右
a[k].w += a[k*2].w+a[k*2+1].w;//求和
}---------------------------------------------------------------------------------------------------------------
延迟标记
这里咱们开始用到上面的变量flag了
上面说了,线段树是支持区间修改的,比如说开始那张图,咱把[1,5]都加上3,总不能把[1,5],[1,3],[4,5],[1,2],[3,3],[4,4],[5,5],[1,1],[2,2]都修改了啊,这样从第二层一直到第四层那我还要这个线段树干嘛,时间早爆炸了.
这时候,精髓部分来了,诶咱就只修改a[2]这个地方,也就是[1,5],下面的暂时用不上,就不管它.然后让flag=3.
如果下一次需要用到这一部分数据的话,将flag下传,这样查询哪一部分咱就算哪一部分的和,其他的就不管
要将[1,5]这部分+3但是不查询他的话,那么[1,5]的左右孩子也就没有更改的必要了
这个flag就是延迟标记,有了它,我们就只需要将修改过的区域标记,等到查询此部分的时候再向下修改就行了
以线段树区间1-10,初值全为0,[1,5]全部+3为例:
可以看出,[1,5]的子区间内的区间和是不对的(修改后不应该为0~)
没关系,我们只需要修改[1,5]和包含[1,5]的区间的内容即可,然后我们让flag = 3,[1,5]的子区间暂时不用管
(黑色数字代表区间和,红色代表flag的值)
如果接下来查询[1,3]或者[1,5]的其他子区间,我们再向下计算区间和,对于查询[1,3]而言,图是这样子的:
结论已经呼之欲出了:
如果查询的区域有延迟标记flag,就将标记下传,并且左右孩子的和+=flag*(左右孩子区间内所存的数)
比如说[1,5]的左孩子区间为1-3,则为3*(3-1+1) = 3*3
具体操作如下
void down(int k) {
a[k*2].flag += a[k].flag; //标记下传
a[k*2+1].flag += a[k].flag;
a[k*2].w += a[k].flag*(a[k*2].r-a[k*2].l+1); //标记求和
a[k*2+1].w += a[k].flag *(a[k*2+1].r-a[k*2+1].l+1);
a[k].flag = 0; //下传之后清空当前节点的标记
}---------------------------------------------------------------------------------------------------------------
区间查询
有了延迟标记的基础我们就可以进行区间求和了
也是比较简单的过程,会二分应该就能看懂
void askinterval(int k,int x,int y) {
if(a[k].l>=x && a[k].r<=y) {
ans += a[k].w; ///ans为全局变量,记得每次查询令ans = 0;
return;
}
if(a[k].flag)
down(k);
int buf = (a[k].l+a[k].r)/2;
if(x <= buf)
askinterval(k*2,x,y); ///递归查左子树
if(y > buf)
askinterval(k*2+1,x,y); ///递归查右子树
}-----------------------------------------------------------------------------------------------------------------
区间修改
区间修改和上面的区间查询代码基本相同,自行研究咯~
void changeinterval(int k,int x,int y,int z) {
if(a[k].l>=x &&a[k].r<=y) {
a[k].w += (a[k].r-a[k].l+1)*z;
a[k].flag += z;
return;
}
if(a[k].flag)
down(k);
int buf = (a[k].l+a[k].r)/2;
if(x <= buf)
changeinterval(k*2,x,y,z);
if(y > buf)
changeinterval(k*2+1,x,y,z);
a[k].w = a[k*2].w + a[k*2+1].w;
}-----------------------------------------------------------------------------------------------------------------
单点查询
其实单点查询完全可以使用上面区间查询的函数,反正都是一样的~
不过毕竟是模板嘛,还是贴一份代码
void askinterval(int k,int x) {
if(a[k].l==x && a[k].r==x) {
ans = a[k].w;
return;
}
if(a[k].flag)
down(k);
int buf = (a[k].l+a[k].r)/2;
if(x <= buf)
askinterval(k*2,x);
if(y > buf)
askinterval(k*2+1,x);
}单点修改
同样,单点修改也可以使用区间修改的代码,只需要让x和y一样就行.
void changeinterval(int k,int x,int z) {
if(a[k].l==x &&a[k].r==x) {
a[k].w += (a[k].r-a[k].l+1)*z;
a[k].flag += z;
return;
}
if(a[k].flag)
down(k);
int buf = (a[k].l+a[k].r)/2;
if(x <= buf)
changeinterval(k*2,x,z);
if(y > buf)
changeinterval(k*2+1,x,z);
a[k].w = a[k*2].w + a[k*2+1].w;
}老规矩,最后一道例题
解题代码如下:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <string>
#include <vector>
#define For(a,b) for(ll a=0;a<b;a++)
#define mem(a,b) memset(a,b,sizeof(a))
#define _mem(a,b) memset(a,0,(b+1)<<2)
#define lowbit(a) ((a)&-(a))
#define IO do{\
ios::sync_with_stdio(false);\
cin.tie(0);\
cout.tie(0);}while(0)
using namespace std;
typedef long long ll;
const ll maxn = 2*1e5+5;
const ll INF = 0x3f3f3f3f;
struct node {
ll l,r,w,flag;
} a[maxn<<2]; //4±¶Êý×é
ll c[maxn];
ll cnt;
void build(ll k,ll l,ll r) {
a[k].l = l,a[k].r = r;
if(a[k].l == a[k].r) {
scanf("%lld",&a[k].w);
//cin >> a[k].w;
return;
}
build(k*2, l, (l+r)/2);
build(k*2+1, (l+r)/2+1, r);
a[k].w = max(a[k*2].w,a[k*2+1].w);
}
void changellerval(ll k,ll x,ll z) {
if(a[k].l==x &&a[k].r==x) {
a[k].w = z;
return;
}
ll buf = (a[k].l+a[k].r)/2;
if(x <= buf)
changellerval(k*2,x,z);
if(x > buf)
changellerval(k*2+1,x,z);
a[k].w = max(a[k*2].w, a[k*2+1].w);
}
ll ans;
void askllerval(ll k,ll x,ll y) {
if(a[k].l>=x && a[k].r<=y) {
ans = max(a[k].w,ans);
return;
}
ll buf = (a[k].l+a[k].r)/2;
if(x <= buf)
askllerval(k*2,x,y);
if(y > buf)
askllerval(k*2+1,x,y);
}
int main() {
//IO;
char buf;
ll n,m;
ll x,y,z;
while(cin >> n >> m) {
build(1,1,n);
For(i,m) {
getchar();
scanf("%c",&buf);
//cin >> buf;
if(buf == 'Q') {
scanf("%lld%lld",&x,&y);
//cin >> x >> y;
ans = 0;
askllerval(1,x,y);
printf("%lld\n",ans);
//cout << ans << endl;
} else {
scanf("%lld%lld",&x,&z);
//cin >> x >> y >> z;
changellerval(1,x,z);
}
}
}
return 0;
}