1、多项式的两种表示法
1.系数表示法
我们最常用的多项式表示法就是系数表示法,一个次数界为\(n\)的多项式\(S(x)\)可以用一个向量\(s=(s_0,s_1,s_2,\cdots,s_n-1)\)系数表示如下:\[S(x)=\sum_{k=0}^{n-1}s_kx^k\]
系数表示法很适合做加法,可以在\(O(n)\)的时间复杂度内完成,表达式为:\[S(x)=A(x)+B(x)=\sum_{k=0}^{n-1}(a_k+b_k)x^k\]
当中\[s_k=a_k+b_k\]
但是,系数表示法不适合做乘法,时间复杂度为\(O(n^2)\),表达式为:\[S(x)=A(x)B(x)=\sum_{k=0}^{n-1}\left(\sum_{j=0}^{n-1}a_j b_{k-j}\right)x^k\]
当中\[s_k=\sum_{j=0}^k a_j b_{k-j}\]
这就是卷积的一般形式,记\(s=a\otimes b\),我们要想办法加速这个过程。
2.点值表示法
顾名思义,点值就是多项式在一个点处的值。多项式\(A(x)\)的点值表达是一个集合:\[\{(x_0,y_0),(x_1,y_1),(x_2,y_2),\cdots,(x_{n-1},y_{n-1})\}\]
使得对于\(k=0,1,2,\cdots,n-1\)有\(x_k\)两两不相同且\(y_k=A(x_k)\)。
\(n\)个点可以确定唯一一个\(n\)次多项式。
点值表达有很多优良的性质,加法和乘法都可以在\(O(n)\)的时间复杂度内完成。
现有\(A(x)\)的点值表达\[\{(x_0,y_0),(x_1,y_1),(x_2,y_2),\cdots,(x_{n-1},y_{n-1})\}\]和\(B(x)\)的点值表达\[\{(x_0,y'_0),(x_1,y'_1),(x_2,y'_2),\cdots,(x_{n-1},y'_{n-1})\}\]
则\(C(x)=A(x)+B(x)\)的点值表达为:\[\{(x_0,y_0+y'_0),(x_1,y_1+y'_1),(x_2,y_2+y'_2),\cdots,(x_{n-1},y_{n-1}+y'_{n-1})\}\]
\(C(x)=A(x)B(x)\)的点值表达为:\[\{(x_0,y_0 y'_0),(x_1,y_1 y'_1),(x_2,y_2 y'_2),\cdots,(x_{n-1},y_{n-1} y'_{n-1})\}\]
可见,点值表示可以帮助我们更快地进行卷积,可是如何在系数表示法和点值表示法之间相互转化呢?
2、复数
当\(x\)为实数时,无法很好地对转换方法进行优化。为了优化计算\(x^n\)所浪费的时间,我们需要\(x\)有循环的性质。但点值表示法需要\(n\)个两两不同的值,而在实数域中只有\(1\)和\(-1\),因此,我们需要复数的帮助。
1.复数、复平面的定义
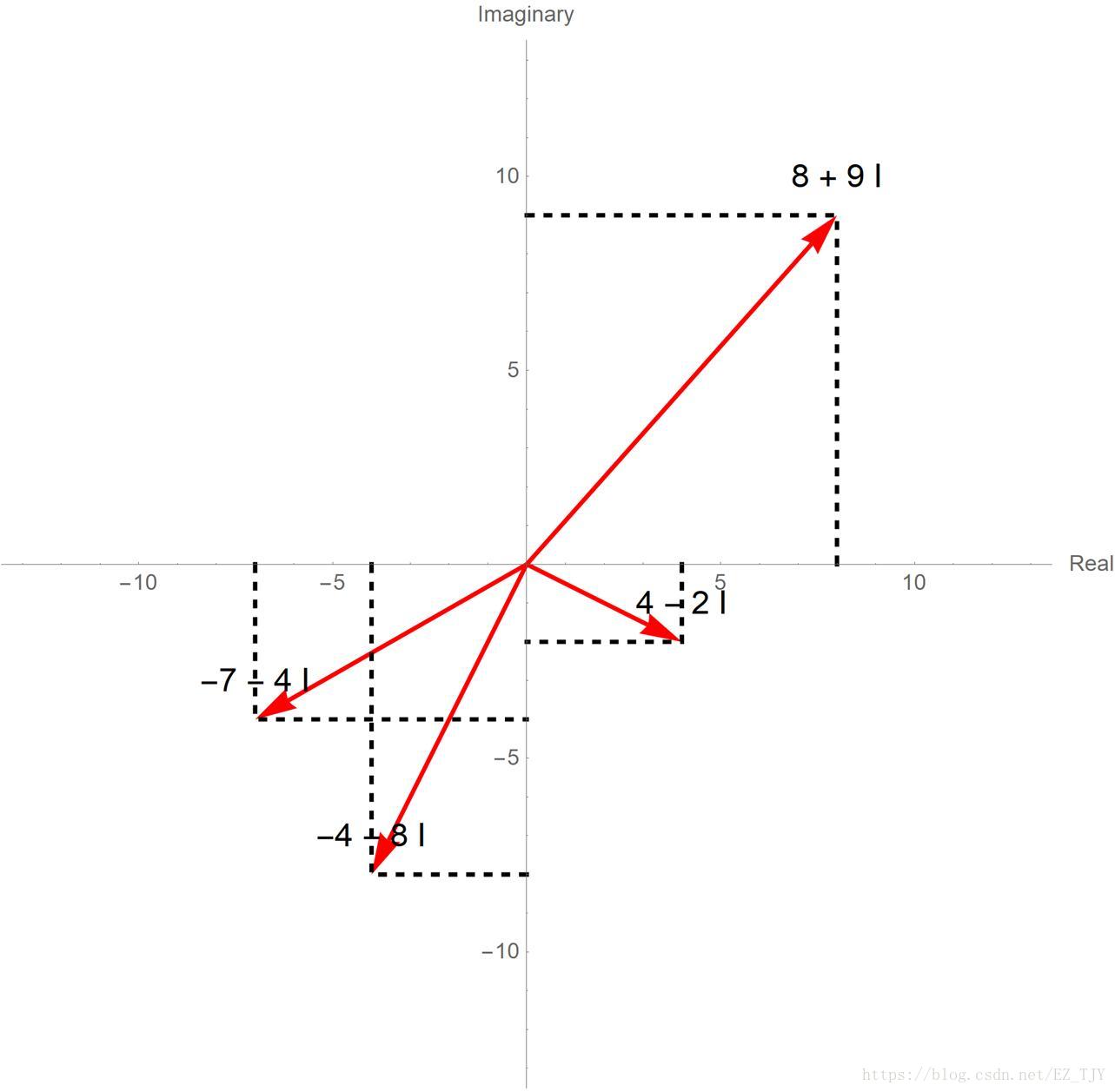
我们把形如\(a+bi\)的数称为复数\(z\),其中\(a\)为实部(Real),记为\(\Re z\);\(b\)为虚部(Imaginary),记为\(\Im z\)。
每一点都对应唯一复数的平面叫复平面,相当于一个把\(\Re z\)作为横坐标,把\(\Im z\)作为纵坐标的笛卡尔坐标系。如图:
模长:复平面上原点到复数\(z\)的距离,记为\(|z|\)。根据勾股定理,\(|z|=|a+bi|=\sqrt{a^2+b^2}\)
辐角:复平面上\(x\)轴与复数\(z\)所对应向量之间的夹角,在\((-\frac{\pi}{2},\frac{\pi}{2})\)之间的记为辐角主值\(\arg z\)。
2.欧拉公式
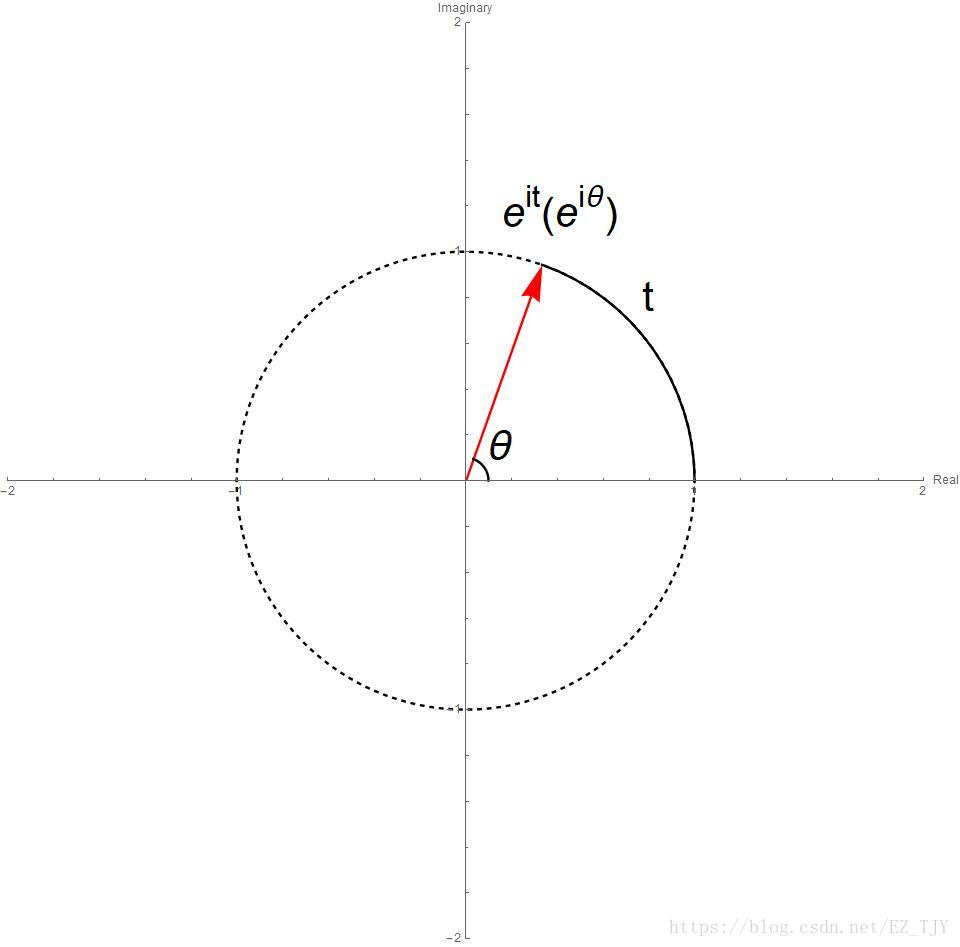
大名鼎鼎的欧拉公式:\[e^{i t}=\cos t+i\sin t\]
根据三角函数在单位圆上的几何意义,公式是容易理解的。
几何意义:
当中\(\theta\)为角度,\(t\)为弧长。
则根据欧拉公式,可将一个复数表示为一个二元组\((a,\theta)\),即模长和辐角(相当于复平面上极坐标系的表示方法)。值为:\(a(\cos\theta+i\sin\theta)\)
特殊情况:欧拉恒等式\(e^{i\pi}+1=0\)
3.复数的运算
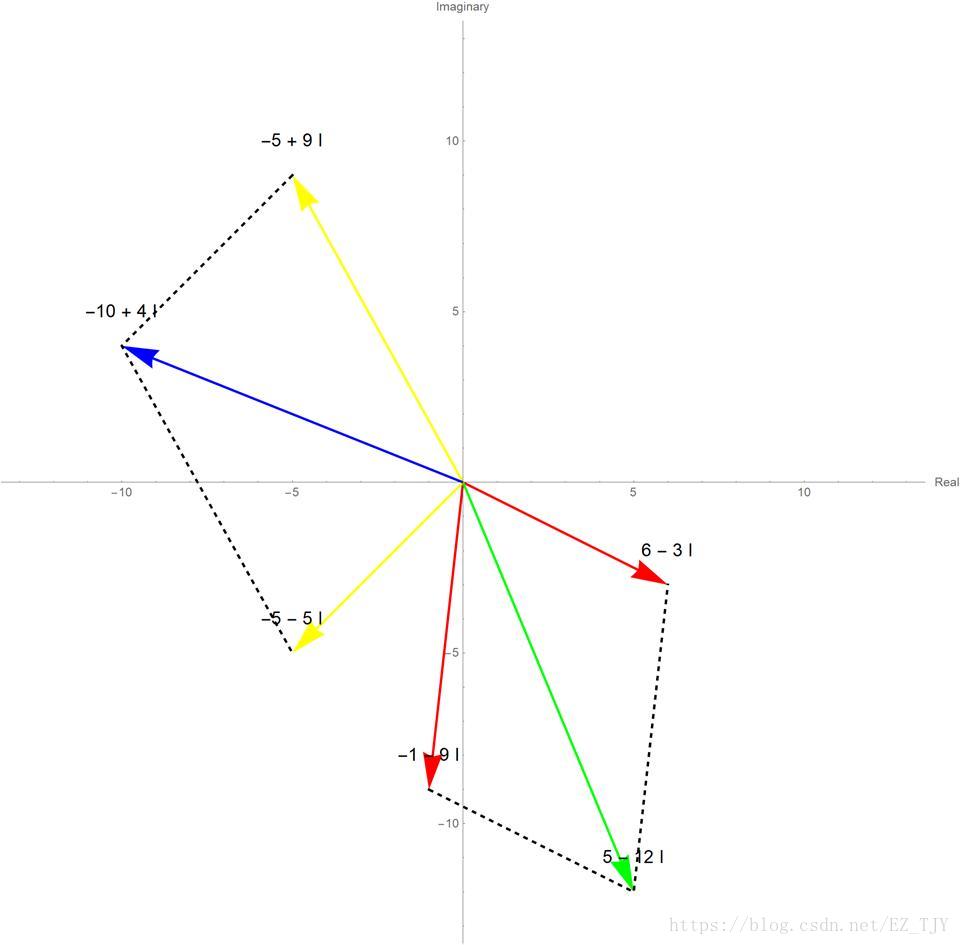
(1)复数加法
运算规则:实部、虚部分别相加\[(a+bi)+(c+di)=a+c+bi+di=(a+c)+(b+d)i\]
几何意义:如图
结果相当于两个向量所构成的平行四边形的对角线。如果把一个复数所对应的向量视为一个移动的变换,那么向量加法就是连续运用这两个变换相当于的新变换。
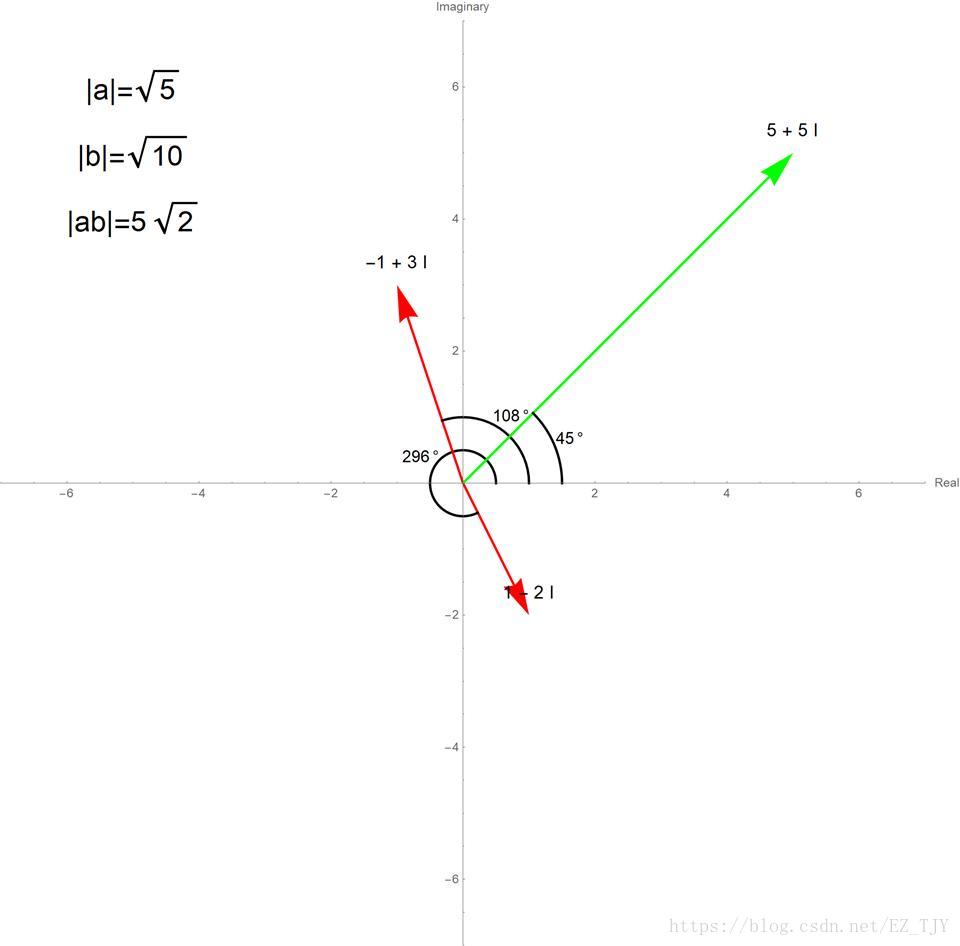
(2)复数乘法
运算规则:展开\[(a+bi)(c+di)=ac+adi+bci+bdi^2=(ac-bd)+(ad+bc)i\]
几何意义:如图
如图,\(\arg a+\arg b=\arg a\times b\),\(|a|\times|b|=|a\times b|\)
总结就是:模长相乘,辐角相加。
因此,如果模长为\(1\),那么它的\(n\)次方一定还在单位圆上。
证明:
根据欧拉公式,已知\(x=(a_1,\theta_1)=a_1(\cos\theta_1+i\sin\theta_1),y=(a_2,\theta_2)=a_2(\cos\theta_2+i\sin\theta_2)\)
则\[\begin{align*} x\times y&=a_1 a_2(\cos\theta_1+i\sin\theta_1)(\cos\theta_2+i\sin\theta_2)\\ &=a_1 a_2\left[(\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2)+i(\cos\theta_1\sin\theta_2+\sin\theta_1\cos\theta_2)\right]\\ &=a_1 a_2\left[\left(\frac{\cos(\theta_1+\theta_2)+\cos(\theta_1-\theta_2)}{2}+\frac{\cos(\theta_1+\theta_2)-\cos(\theta_1-\theta_2)}{2}\right)\right.\\ &\left.+i\left(\frac{\sin(\theta_1+\theta_2)-\sin(\theta_1-\theta_2)}{2}+\frac{\sin(\theta_1+\theta_2)+\sin(\theta_1-\theta_2)}{2}\right)\right]\tag{积化和差公式}\\ &=a_1 a_2\left[\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\right] \end{align*}\]
\(\therefore |x\times y|=|x|\times |y|,\arg(x\times y)=\arg x+\arg y\)
证毕。
4.单位复数根
(1)基本性质
单位复数根是方程\(\omega^n=1\)的解,第\(k\)个解记为\(\omega_n^k\)(这里的\(k\)事实上是乘方的含义)
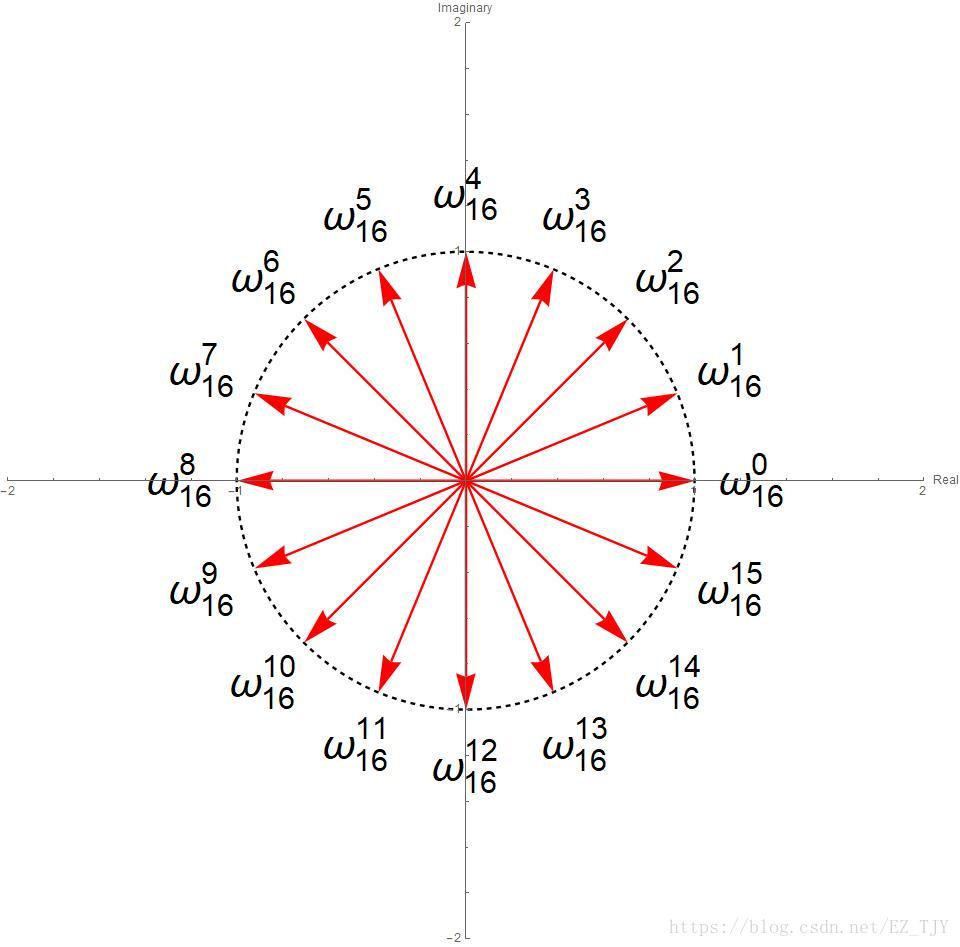
\(n=16\)的解在复平面上的位置如下:
可以看到,\(n\)个解把单位圆分成了\(n\)等弧,交点即为根。而且,\(\omega_n^k\)实际上是\(\omega_n\)的\(n\)次方,模长仍为\(1\),辐角翻倍!
为什么呢?
\(\because |x^n|=|x|^n,\arg x^n=n\arg x\)
\(\therefore |\omega|^n=|\omega^n|,\arg\omega^n=n\arg\omega\)
\(\therefore |\omega|^n=1(|\omega|\in\mathbb{R}^+),\arg\omega=\frac{360^\circ}{n}\)
\(\therefore |\omega|=1,\arg\omega=\frac{360^\circ}{n}\)
这就很明显了。
所以,\(\omega_n^k\)事实上表示的是\(\omega_n\)的\(k\)次幂。为什么选择单位复数根呢?因为它有循环的优良性质,即\(\omega_n^n=1\)。由于其他的都可以由\(\omega_n^1\)得到,因此称为主\(n\)次单位根,又记为\(\omega_n\)。
根据单位复数根的平分圆的意义和欧拉公式,\(\omega_n^k=e^\frac{2\pi i k}{n}=\cos\frac{2\pi k}{n}+i\sin\frac{2\pi k}{n}\)。
(2)计算引理
显然,由于单位复数根循环(\(\omega_n^{zn}=e^{2\pi iz}=\left[\left(e^{\pi i}\right)^2\right]^z=1^z=1\)),有变换恒等式:\[\omega_n^k=\omega_n^{k+wn}(w\in\mathbb{Z})\]
每一份再分成\(k\)份,编号也变成\(k\)倍,位置自然不变(\(\omega_{d n}^{d k}=e^\frac{2\pi i d k}{dn}=e^\frac{2\pi i k}{n}=\omega_n^k\)),所以有消去引理:\[\omega_{d n}^{d k}=\omega_n^k\]
由于过了\(n/2\)就会绕过半圈(\(\omega_n^{n/2}=e^\frac{\pi i n}{n}=e^{\pi i}=-1\)),所以有折半引理:\[\omega_n^k=-\omega_n^{k\pm n/2}\]
对单位复数根求和,根据几何级数(等差数列求和公式),可得(\(\sum\limits_{k=0}^{n-1}(\omega_n^k)^j=\frac{(\omega_n^n)^j-1}{\omega_n^1-1}=0\)),即有求和引理(要注意公式的使用条件):\[\sum_{k=0}^{n-1}(\omega_n^k)^j=0,\omega_n^k\ne 1\]
3、DFT&FFT
1.DFT
DFT就是求多项式\(A(x)\)在点\((\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1})\)处取值的过程。即:\[y_k=A(\omega_n^k)=\sum_{j=0}^{n-1}a_j\omega_n^{kj}\]
结果\(y=(y_0,y_1,y_2,\cdots,y_{n-1})\)就是\(a\)的离散傅里叶变换(DFT),记为\(y=DFT_n(a)\)
2.FFT
(1)递归
DFT的\(O(n^2)\)算法太慢了,FFT使用分治策略优化速度到\(O(n\log n)\)。
考虑奇偶分治。
现在,我们假设\(n=2^t\),设原系数\(a=(a_0,a_1,a_2,\cdots,a_{n-1})\),分治为偶数部分\(a_1=(a_0,a_2,a_4,\cdots,a_{n-2})\),奇数部分\(a_2=(a_1,a_3,a_5,\cdots,a_{n-1})\),已经递归求出\(y_1=DFT_{n/2}(a_1)\),\(y_2=DFT_{n/2}(a_2)\),现在我们要合并\(y_1,y_2\),得到\(y=DFT_n(a)\)(蝴蝶操作)。
对于\(n=1\)的边界情况,结果是显然的:因为\(k=0\),故\(\omega_1^0=1\),即结果等于原系数。
对于\(n>1\),现在我们枚举\(k\in[1,n]\)要合并出\(y_k\):
\[\begin{align*} y_k&=A(\omega_n^k)\\ &=\sum_{j=0}^{n-1}a_j\omega_n^{kj}\\ &=\sum_{j=0}^{n/2-1}a_{2 j}\omega_n^{2 k j}+\sum_{j=0}^{n/2-1}a_{2 j+1}\omega_n^{2 k j+k}\\ &=\sum_{j=0}^{n/2-1}a_{2 j}\omega_n^{2 k j}+\omega_n^k\sum_{j=0}^{n/2-1}a_{2 j+1}\omega_n^{2 k j}\\ &=\sum_{j=0}^{n/2-1}a_{1_j}\omega_{n/2}^{k j}+\omega_n^k\sum_{j=0}^{n/2-1}a_{2_j}\omega_{n/2}^{k j}\tag{消去引理} \end{align*}\]
对于\(k<n/2\):
\[\begin{align*} y_k&=y_{1_k}+\omega_n^k y_{2_k} \end{align*}\]对于\(k\geq n/2\):
\[\begin{align*} y_k&=\sum_{j=0}^{n/2-1}a_{1_j}\omega_{n/2}^{(k-n/2)j}+\omega_n^k\sum_{j=0}^{n/2-1}a_{2_j}\omega_{n/2}^{(k-n/2)j}\tag{变换恒等式}\\ &=y_{1_{k-n/2}}+\omega_n^k y_{2_{k-n/2}}\\ &=y_{1_{k-n/2}}-\omega_n^{k-n/2}y_{2_{k-n/2}}\tag{折半引理} \end{align*}\]
我们用\(k+n/2\)替代\(k\),就得到\(y_{k+n/2}=y_{1_k}-\omega_n^k y_{2_k}\)
结合在一起就得到\(\begin{cases}y_k&=y_{1_k}+\omega_n^k y_{2_k}\\y_{k+n/2}&=y_{1_k}-\omega_n^k y_{2_k}\end{cases}\)
这样我们就可以把两个\(n/2\)长的序列合并为一个\(n\)长的序列了。
以下图的递归序,就可以在\(O(n\log n)\)的时间复杂度内完成求解了。
(2)迭代
递归方法消耗内存、时间过大,无法承受。我们每次把下标分为奇数部分和偶数部分,是否有办法直接求出最后的递归运算顺序,以避免递归呢?
这样想:
第一次奇偶划分,我们按照二进制的倒数第一位排序;
第二次奇偶划分,我们按照二进制的倒数第二位排序;
第\(n\)次奇偶划分,我们按照二进制的倒数第\(n\)位排序;
依此类推。
因此,结果顺序就是原序列按照二进制位翻转的大小排序的结果。只要依次交换\(a_k,a_{rev(k)}\),求出序列,就可以用迭代方法相邻归并实现快速傅里叶变换。
或者,我们也可以用更加代数的方法来发现这个结论。
已知现在位置为\(k=(b_1 b_2 b_3 \cdots b_n)_2\),按照奇偶重排:
- 若\(b_n=0\),则位置变为\(\frac{k}{2}=(0 b_1 b_2 \cdots b_{n-1})_2=(b_n b_1 b_2 \cdots b_{n-1})_2\),即为把最后一位提到第一位。
- 若\(b_n=1\),则位置变为\(2^{n-1}-1+\frac{k+1}{2}=\frac{2^n+k-1}{2}=\frac{(1 b_1 b_2 \cdots b_{n-1} 0)_2}{2}=(b_n b_1 b_2 \cdots b_{n-1})_2\),同样是把最后一位提到第一位。
则反复\(n\)次之后,就相当于二进制反转了。
如\(n=8\)时,求出二进制:
|0|1|2|3|4|5|6|7|
|:|:|:|:|:|:|:|:|
|\(000_2\)|\(001_2\)|\(010_2\)|\(011_2\)|\(100_2\)|\(101_2\)|\(110_2\)|\(111_2\)|
翻转:
|0|1|2|3|4|5|6|7|
|:|:|:|:|:|:|:|:|
|\(000_2\)|\(100_2\)|\(010_2\)|\(110_2\)|\(001_2\)|\(101_2\)|\(011_2\)|\(111_2\)|
按翻转后的值排序:
|0|4|2|6|1|5|3|7|
|:|:|:|:|:|:|:|:|
|\(000_2\)|\(001_2\)|\(010_2\)|\(011_2\)|\(100_2\)|\(101_2\)|\(110_2\)|\(111_2\)|
这样就可以把奇偶合并转化为左右归并,迭代实现了。
5、IDFT&IFFT
何把点值表达变回系数表达呢?如果把求值写成矩阵形式,就是:
\[\begin{bmatrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0 \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1} \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)} \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)^2} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{bmatrix}= \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix}\]
如果我们要把\(y\)变成\(a\),就需要求出第一个矩阵的逆,即:
\[\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{bmatrix}= \begin{bmatrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0 \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1} \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)} \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)^2} \end{bmatrix}^{-1} \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix}\]
这个范德蒙德矩阵极为特殊,它的逆矩阵是:
\[\begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_{n-1} \end{bmatrix}=\frac{1}{n} \begin{bmatrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0 \\ \omega_n^0 & \omega_n^{-1} & \omega_n^{-2} & \omega_n^{-3} & \cdots & \omega_n^{-(n-1)} \\ \omega_n^0 & \omega_n^{-2} & \omega_n^{-4} & \omega_n^{-6} & \cdots & \omega_n^{-2(n-1)} \\ \omega_n^0 & \omega_n^{-3} & \omega_n^{-6} & \omega_n^{-9} & \cdots & \omega_n^{-3(n-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{-(n-1)} & \omega_n^{-2(n-1)} & \omega_n^{-3(n-1)} & \cdots & \omega_n^{-(n-1)^2} \end{bmatrix} \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_{n-1} \end{bmatrix}\]
只是把每项取倒数,并将结果除以\(n\)即可。
证明:
记原矩阵为\(A_{n n}\),我们给出的矩阵为\(B_{n n}\)。
\(\therefore A_{i j}=\omega_n^{i j},B_{i j}=\frac{1}{n}\omega_n^{-i j}(0\le i,j\le n-1)\)
\[\begin{align*} AB_{i j}&=\sum_{k=0}^{n-1} A_{i k}B_{k j}\\ &=\frac{1}{n}\sum_{k=0}^{n-1} \omega_n^{i k}\omega_n^{-k j}\\ &=\frac{1}{n}\sum_{k=0}^{n-1} \omega_n^{i k-k j}\\ &=\frac{1}{n}\sum_{k=0}^{n-1} (\omega_n^{i-j})^k \end{align*}\]
- 当\(i=j\)时:
\[\begin{align*} AB_{i j}&=\frac{1}{n}\sum_{k=0}^{n-1}1^k\\ &=\frac{1}{n}\times n\\ &=1 \end{align*}\]
- 当\(i\ne j\)时:
\[\begin{align*} AB_{i j}&=\frac{1}{n}\sum_{k=0}^{n-1}(\omega_n^{i-j})^k\\ &=0\tag{求和引理} \end{align*}\]
综上所述,\(AB=I_n\),即\(B=A^{-1}\)
以上,离散傅里叶逆变换(IDFT)的表达式为:\[a_k=\frac{1}{n}\sum_{j=0}^{n-1}y_k\omega_n^{-k j}\]
记\(a=IDFT_n(y)\)。
同理,可以用相同的方法把IDFT加速到\(O(n\log n)\),称为IFFT。
5、NTT
1.定义
有时候我们会想要模素数\(p\)意义下的多项式乘法。此时,由次数界为\(n\)的多项式\(A(x),B(x)\)的系数表达\(a,b\)求\(S(x)=A(x)B(x)\)的系数表达\(s\)的公式为:\[s_k=\sum_{j=0}^k a_j b_{k-j}\mod p\]
FFT无能为力,我们需要一种新的DFT,以数论的办法进行,这就是快速数论变换(NTT)。
2.原根
(1)定义
我们需要一种有数论循环性质的新数,原根恰好满足我们的要求。
设\(m\)为正整数,\(a\)为整数,若\(a\)模\(m\)的阶等于\(\varphi(m)\),则称\(a\)为模\(m\)的一个原根。
假设\(g\)是素数\(p\)的原根,有\(1<g<p\),且对于\(k=0,1,2,\cdots,p-1\),有\(g^k\mod p\)的结果两两不同,且\(g^{p-1}\equiv 1 \pmod p\)。
可以发现,原根同样有循环的性质。因此,我们类比\(\omega_n^k\)的定义,把原来的\(\omega_n^k=e^\frac{2\pi ik}{n}\)替换为\(g^\frac{k(p-1)}{n}\)。
(2)性质
我们来证明一些类似单位复数根的性质。
变换恒等式:
因为:\[g^{p-1}\equiv 1\]
所以:\[g^\frac{(k+n)(p-1)}{n}\equiv g^\frac{k(p-1)}{n}g^{p-1}\equiv g^\frac{k(p-1)}{n}\]
消去引理:
显然有:\[g^\frac{d k(p-1)}{d n}\equiv g^\frac{k(p-1)}{n}\]
折半引理:
因为:\[g^\frac{(k+\frac{n}{2})(p-1)}{n}\equiv g^\frac{k(p-1)}{n}g^\frac{p-1}{2}\]
所以若要使:\[g^\frac{k(p-1)}{n}+g^\frac{(k+\frac{n}{2})(p-1)}{n}\equiv 0\pmod p\]
成立,即:\[g^\frac{k(p-1)}{2}\left(1+g^\frac{p-1}{2}\right)\equiv 0\]
只需证:\[g^\frac{p-1}{2}\equiv p-1\]
由于:\[g^{k}\equiv 0,1,2,\cdots,p-1\]
那么我们可以设:\[g^\frac{p-1}{2}\equiv x,x=0,1,2,\cdots,p-1\]
因为:\[\left(g^\frac{p-1}{2}\right)^2\equiv g^{p-1}\equiv 1\]
所以:\[x^2-1\equiv 0\]
即:\[(x+1)(x-1)\equiv 0\]
又因为\(p\)为素数,所以有:\[x+1\equiv 0\;或\;x-1\equiv 0\]
所以:\[x=1,p-1\]
又因为:\[g^{p-1}\equiv 1,g^k\mod p两两不同\]
所以:\[x=p-1\]
即:\[g^\frac{p-1}{2}\equiv p-1\]
得证:\[g^\frac{k(p-1)}{n}+g^\frac{(k+\frac{n}{2})(p-1)}{n}\equiv 0\]
求和引理:
\[\sum\limits_{k=0}^{n-1}g^\frac{k j(p-1)}{n}\equiv\sum\limits_{k=0}^{n-1}\left(g^\frac{j(p-1)}{n}\right)^k\equiv\frac{g^\frac{n j(p-1)}{n}-1}{g^\frac{j(p-1)}{n}-1}\equiv\frac{\left(g^{p-1}\right)^j-1}{g^\frac{j(p-1)}{n}-1}\equiv 0\]
这样,我们就证明了原根由于复数单位根相同的性质。
3.公式
我们用原根替换复数单位根,得到:\[y_k=A(g^\frac{k(p-1)}{n})=\sum_{j=0}^{n-1}a_k g^\frac{k j(p-1)}{n}\]
即\(y=NTT_n(a)\)。逆变换:\[a_k=\frac{1}{n}\sum_{j=0}^{n-1}y_k g^\frac{-k j(p-1)}{n}\]
即\(a=INTT_n(y)\)。
6、其他扩展
1.任意模数FFT
有的时候我们需要卷积后模上一个数,这个数不是NTT模数,甚至可能不是个质数。那我们该怎么做呢?
这里使用拆系数FFT,本质是以时间换精度。
现在给定次数界为\(m\)的两个多项式\(A(x),B(x)\),要求\(A(x)B(x) \mod P\)。
首先,令\(M=\lfloor\sqrt{P}\rfloor\),再对于每个\(a_i\)或\(b_i\),把其变为\(k_i M+r_i(r_i<M)\)的形式。这样,\(k_i\)和\(r_i\)就都小于等于\(M\)了。
那么卷积就可以写成:\[c_i=\sum_{k=0}^i a_k b_{i-k}=\sum_{k=0}^i(k_{a_i}M+r_{a_i})(k_{b_{i-k}}M+r_{b_{i-k}})=M^2\sum_{k=0}^i k_{a_i}k_{b_{i-k}}+M\sum_{k=0}^i (k_{a_i}r_{b_{i-k}}+r_{a_i}k_{b_{i-k}})+\sum_{k=0}^i r_{a_i}r_{b_{i-k}}\]
那么我们看到,\(c_i\)可以由\(k\)和\(r\)合并得到。那么我们对\(k_a,k_b,r_a,r_b\)分别做FFT,再对应算出\(x_1=k_a k_b,x_2=k_a r_b+r_a k_b,x_3=r_a r_b\),对它们再分别做IFFT,就可以由\(c=M^2 x_1+M x_2+x_3\)得到答案了。
这么做的好处究竟在哪里呢?事实上,计算后的最大值由\(m P\)变为了\(m \lfloor\sqrt{P}\rfloor\),避免了溢出。
时间复杂度:\(O(n\log n)\)
2.多项式求逆
现在我们有一个次数界为\(n\)的多项式\(A(x)\),要求\(B(x)\)满足\(A(x)B(x)\equiv 1\pmod{x^n}\)。
我们考虑倍增实现。
- 当\(n=1\)时,直接求逆元求得\(B(x)\equiv A(x)^{p-2}\)。
- 当\(n>1\)时,已有\(A(x)G(x)\equiv 1\pmod{x^\frac{n}{2}}\):
因为:\[A(x)B(x)\equiv 1\pmod{x^n}\]
又因为除了\(0\)次项之外到\(n-1\)次都为\(0\),因此到\(\frac{n}{2}-1\)次项也为零:\[A(x)B(x)\equiv 1\pmod{x^\frac{n}{2}}\]
又\[A(x)G(x)\equiv 1\pmod{x^\frac{n}{2}}\]
两式相减:\[A(x)[B(x)-G(x)]\equiv 0\pmod{x^\frac{n}{2}}\]
因为:\[A(x)\ne 0\]
所以:\[B(x)-G(x)\equiv 0\pmod{x^\frac{n}{2}}\]
既然\(0\)至\(\frac{n}{2}-1\)次项都为零,那么平方之后\(0\)至\(n-1\)次项也为零:\[B(x)^2-2 B(x)G(x)+G(x)^2\equiv 0\pmod{x^n}\]
又\[A(x)B(x)\equiv 1\pmod{x^n}\]
两边同时乘上\(A(x)\),得:\[B(x)-2 G(x)+A(x)G(x)^2\equiv 0\pmod{x^n}\]
移项,得:\[B(x)\equiv 2 G(x)-A(x)G(x)^2\pmod{x^n}\]
这样就可以了。
时间复杂度:\(O(n\log n)\)
3.多项式开根
前置:多项式求逆。
现在我们有一个次数界为\(n\)的多项式\(A(x)\),要求\(B(x)\)满足\(B(x)^2\equiv A(x)\pmod{x^n}\)。
还是倍增。
- 当\(n=1\)时,\(B(x)\)等于\(A(x)\)在模意义下的开根。
- 当\(n>1\)时,已有\(G(x)^2\equiv A(x)\pmod{x^\frac{n}{2}}\):
因为:\[G(x)^2\equiv A(x)\pmod{x^\frac{n}{2}}\]
移项,得:\[G(x)^2-A(x)\equiv 0\pmod{x^\frac{n}{2}}\]
两边平方,同理可得:\[G(x)^4-2 G(x)^2 A(x)+A(x)^2\equiv 0\pmod{x^n}\]
所以:\[[G(x)^2+A(x)]^2-4 G(x)^2 A(x)\equiv 0\pmod{x^n}\]
即:\[[G(x)^2+A(x)]^2\equiv 4 G(x)^2 A(x)\pmod{x^n}\]
除过去:\[\frac{[G(x)^2+A(x)]^2}{4 G(x)^2}\equiv A(x)\pmod{x^n}\]
得到:\[A(x)\equiv\left(\frac{G(x)^2+A(x)}{2 G(x)}\right)^2\equiv B(x)^2\pmod{x^n}\]
即:\[B(x)\equiv\frac{G(x)^2+A(x)}{2 G(x)}\equiv\frac{A(x)}{2 G(x)}+\frac{G(x)}{2}\pmod{x^n}\]
这就可以了。
时间复杂度:\(O(n\log n)\)
4.多项式求导
根据导数的可加性和幂函数求导法则\(\frac{\mathbb{d}(cx^k)}{\mathbb{d}x}=c k x^{k-1}\),有多项式的导数为:\[\frac{\mathbb{d}(\sum\limits_{k=0}^{n-1}a_k x^k)}{\mathbb{d} x}=\sum_{k=0}^{n-1}\frac{\mathbb{d}(a_k x^k)}{\mathbb{d} x}=\sum_{k=1}^{n-1}k a_k x^{k-1}=\sum_{k=0}^{n-2}(k+1)a_{k+1}x^k\]
时间复杂度:\(O(n)\)
5.多项式积分
根据积分的可加性和幂函数的不定积分\(\displaystyle\int c x^k\mathbb{d}x=\frac{c}{k}x^{k+1}\),有多项式的不定积分为:\[\int\sum_{k=0}^{n-1}a_k x^k \mathbb{d}x=\sum_{k=0}^{n-1}\int a_k x^k\mathbb{d}x=\sum_{k=0}^{n-1}\frac{a_k}{k}x^{k+1}=\sum_{k=1}^n\frac{a_{k-1}}{k-1}x^k\]
时间复杂度:\(O(n)\)
6.多项式求ln
前置:多项式求导&积分&求逆
现在已知多项式\(A(x)\),要求\(B(x)=\ln A(x)\)。我们两边微分,得到:\[B'(x)=\frac{\mathbb{d}(\ln A(x))}{\mathbb{d} A(x)}\frac{\mathbb{d} A(x)}{\mathbb{d} x}\]
\[B'(x)=\frac{A'(x)}{A(x)}\]
再两边积分,就得到:\[B(x)=\int\frac{A'(x)}{A(x)}\mathbb{d}x\]
因此,我们直接多项式求导+求逆+积分解决。
时间复杂度:\(O(n\log n)\)
7.多项式求exp
前置:多项式求ln
现在,我们已知多项式\(A=A(x)\)(这样写是因为在这里把\(A\)视为是与\(x\)无关的),求\(F(x)=\exp(A)=e^{A}\)。只要我们设\(G(x)=\ln x-A\),就得到:\[G(F(x))=\ln F(x)-A=0\]
我们考虑用牛顿迭代法来倍增解这个方程。
对于牛顿迭代法的初始解,即结果的常数项,我们并不知道具体值。但是如果不对的话,也只是缺少了一个常数罢了,那我们不妨设\(F(x)=1\)。
倍增:现在设我们已经求出了\(F(x)\)的前\(n\)项\(F_0(x)\),即:\[F_0(x)\equiv F(x)\pmod{x^n}\]
根据牛顿迭代法,我们求出下一个近似解为:\[F(x)\equiv F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))}\equiv F_0(x)-\frac{\ln F_0(x)-A}{F_0(x)^{-1}}\equiv F_0(x)(1-\ln F_0(x)+A(x))\]
如此,就可以倍增实现了。
时间复杂度:\(O(n\log n)\)
8.多项式求幂
已知多项式\(A(x)\)和指数\(k\),求\(A(x)^k\)。
在幂数很大的时候,为了确定出系数,时间复杂度为\(O(k n \log (nk))\),我们必须进行优化。
我们发现:\[A(x)^k=\left(e^{\ln A(x)}\right)^k=e^{k \ln A(x)}=\exp(k \ln A(x))\]
于是我们可以用多项式求ln+多项式求exp在\(O(n \log n)\)的时间内求出。
7、代码实现
1.二进制反转
可以用一种类似dp的思想计算。
边界:\(0\)的二进制翻转为\(0\)
递归式:对于\(a\),已经算出了\(rev_{\lfloor\frac{a}{2}\rfloor}\),\(a\)就是除去最后一位的二进制翻转(\(rev_{\lfloor\frac{a}{2}\rfloor}\))向后移动一位再补上第一位。即:
rev[a]=(rev[a>>1]>>1)|((a&1)<<(l-1))\(l\)为要翻转的位数。
2.复数类
套公式即可。
struct complex{
double re,im;
complex(double re=0,double im=0):re(re),im(im){}
complex operator+(complex &b)const{return complex(re+b.re,im+b.im);}
complex operator-(complex &b)const{return complex(re-b.re,im-b.im);}
complex operator*(complex &b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
};3.FFT
- 1:根据二进制翻转交换\(a_r\)和\(a_{rev(r)}\)
- 2:枚举归并步长\(i\in[1,n)\),\(i\)为二的幂;
- 2.1: 根据欧拉公式求出\(\omega_i^1=\cos\frac{\pi}{i}+i\sin\frac{\pi}{i}\)
- 2.2:枚举归并位置\(j\),归并\([j,j+i)\)和\([j+i,j+2 i)\),步长为\(2 i\)
- 2.2.1:枚举\(x\)的幂数\(k\in[0,i)\)进行蝴蝶操作计算\(y\),根据单位根计算\(\omega_i^k\)
- 2.2.1.1:\(y_{j+k}=y_{j+k}+\omega_i^k y_{j+k+i}\)
- 2.2.1.2:\(y_{j+k+i}=y_{j+k}-\omega_i^k y_{j+k+i}\)
- 2.2.1:枚举\(x\)的幂数\(k\in[0,i)\)进行蝴蝶操作计算\(y\),根据单位根计算\(\omega_i^k\)
注意:由于在C++中值会被更改,因此需要引入临时变量。
void FFT(complex c[]){
for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
for(int i=1;i<n;i<<=1){
complex omn(cos(pi/i),sin(pi/i));
for(int j=0;j<n;j+=(i<<1)){
complex om(1,0);
for(int k=0;k<i;k++,om=om*omn){
complex x=c[j+k],y=om*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}4.IFFT
由于公式中只差一个负号而已,因此引入一个参数\(type\),在欧拉公式的地方乘上去,再除以\(n\)就可以了。
void FFT(complex c[],int tp=1){
for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
for(int i=1;i<n;i<<=1){
complex omn(cos(pi/i),tp*sin(pi/i));
for(int j=0;j<n;j+=(i<<1)){
complex om(1,0);
for(int k=0;k<i;k++,om=om*omn){
complex x=c[j+k],y=om*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}
void IFFT(complex c[]){
FFT(c,-1);
for(int i=0;i<=m;i++)a[i].re/=n;
}5.多项式乘法
模板:洛谷3083
注意:
1、由于FFT要求\(n\)为\(2\)的幂且结果的次数界较大,所以要把两个因式的系数补到\(l\)位,\(l\)满足\(l=2^t\)且\(l/2\)大于等于因式的次数界。
2、\(FFT\)虽然在数学上精准,但在C++中误差巨大,因此虚部不会为\(0\),忽略即可。实部也不为正数,可以加上\(0.1\)再向下取整。
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const double pi=acos(-1);
struct complex{
double re,im;
complex(double re=0,double im=0):re(re),im(im){}
complex operator+(complex &b)const{return complex(re+b.re,im+b.im);}
complex operator-(complex &b)const{return complex(re-b.re,im-b.im);}
complex operator*(complex &b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
}a[2097153],b[2097153];
int n,m,l,r[2097153];
void FFT(complex c[],int tp=1){
for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
for(int i=1;i<n;i<<=1){
complex omn(cos(pi/i),tp*sin(pi/i));
for(int j=0;j<n;j+=(i<<1)){
complex om(1,0);
for(int k=0;k<i;k++,om=om*omn){
complex x=c[j+k],y=om*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}
void IFFT(complex c[]){
FFT(c,-1);
for(int i=0;i<=m;i++)a[i].re/=n;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++)scanf("%lf",&a[i].re);
for(int i=0;i<=m;i++)scanf("%lf",&b[i].re);
m+=n;
for(n=1;n<=m;n<<=1)l++;
for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
FFT(a);
FFT(b);
for(int i=0;i<=n;i++)a[i]=a[i]*b[i];
IFFT(a);
for(int i=0;i<=m;i++)printf("%d ",int(a[i].re+0.5));
}6.(I)FFT+(I)NTT
给出一个\(n\)次多项式和一个\(m\)次多项式的系数表达(\(1\le n,m\le 4000000\)),求乘积。\(type=0\)时,直接计算;\(type=1\)时,结果取模\(998244353\)(原根为\(3\))。
注:为了方便阅读,代码效率不高。若要提速,可以把单位根打表。而且,由于\(g^\frac{p-1}{n}\)中\(\frac{p-1}{n}\)必须为整数,故仅在第一个比\(n+m\)大的\(2\)的整数次幂是\(p-1\)的约数时才可行,此处\(998244353-1=998244352=119\times2^{23}\),\(2^{23}=8388608>n+m\)。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const double pi=acos(-1);
const int p=998244353;
typedef long long ll;
struct complex{
double re,im;
complex(double re=0,double im=0):re(re),im(im){}
complex operator+(complex b)const{return complex(re+b.re,im+b.im);}
complex operator-(complex b)const{return complex(re-b.re,im-b.im);}
complex operator*(complex b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
}af[131073],bf[131073];
struct modp{
int a;
modp(int a=0):a(a){}
modp operator+(modp b)const{return (a+b.a)%p;}
modp operator-(modp b)const{return (a-b.a+p)%p;}
modp operator*(modp b)const{return ll(a)*b.a%p;}
modp operator/(modp b)const{return (b^(p-2))*a;}
modp operator^(int b)const{
modp ans=1,bs=a;
while(b){
if(b&1)ans=ans*bs;
bs=bs*bs;
b>>=1;
}
return ans;
}
}an[131073],bn[131073];
const modp g=3;
int n,m,l,r[131073],type;
modp gn[18];
void init(){
m+=n;
for(n=1;n<=m;n<<=1)l++;
for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
for(int i=0;i<=17;i++)gn[i]=g^((p-1)/(1<<i));
}
void FFT(complex c[],int tp=1){
for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
for(int i=1;i<n;i<<=1){
complex omn(cos(pi/i),tp*sin(pi/i));
for(int j=0;j<n;j+=(i<<1)){
complex om(1,0);
for(int k=0;k<i;k++,om=om*omn){
complex x=c[j+k],y=om*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}
void IFFT(complex c[]){
FFT(c,-1);
for(int i=0;i<=n;i++)c[i].re/=n;
}
void NTT(modp c[],int tp=1){
for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
for(int i=1,id=1;i<n;i<<=1,id++){
modp ggn=gn[id]^(tp==1?1:p-2);
for(int j=0;j<n;j+=(i<<1)){
modp gg=1;
for(int k=0;k<i;k++,gg=gg*ggn){
modp x=c[j+k],y=gg*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}
void INTT(modp c[]){
NTT(c,-1);
for(int i=0;i<=n;i++)c[i]=c[i]/n;
}
int main(){
scanf("%d%d%d",&n,&m,&type);
if(type==0){
for(int i=0;i<=n;i++)scanf("%lf",&af[i].re);
for(int i=0;i<=m;i++)scanf("%lf",&bf[i].re);
}else{
for(int i=0;i<=n;i++)scanf("%d",&an[i].a);
for(int i=0;i<=m;i++)scanf("%d",&bn[i].a);
}
init();
if(type==0){
FFT(af);
FFT(bf);
for(int i=0;i<=n;i++)af[i]=af[i]*bf[i];
IFFT(af);
for(int i=0;i<=m;i++)printf("%d ",int(af[i].re+0.5));
}else{
NTT(an);
NTT(bn);
for(int i=0;i<=n;i++)an[i]=an[i]*bn[i];
INTT(an);
for(int i=0;i<=m;i++)printf("%d ",an[i].a);
}
printf("\n");
}常数只有上面那个的三分之一的NTT(正式考试请务必采用这种写法):
PS:有一道题上面那个3700ms,这个1000ms
inline ll pow(ll a,int b){
ll ans=1;
while(b){
if(b&1)ans=ans*a%p;
a=a*a%p;
b>>=1;
}
return ans;
}
inline ll add(ll a,ll b){return a+b>p?a+b-p:a+b;}
inline ll cut(ll a,ll b){return a-b<0?a-b+p:a-b;}
void init(){
for(n=1;n<=s;n<<=1);
nn=n;
gn[0][0]=gn[1][0]=1;
gn[0][1]=pow(g,(p-1)/(n<<1));
gn[1][1]=pow(gn[0][1],p-2);
for(int i=2;i<(n<<1);i++){gn[0][i]=gn[0][i-1]*gn[0][1]%p;gn[1][i]=gn[1][i-1]*gn[1][1]%p;}
inv[1]=1;
for(int i=2;i<=(n<<1);i++)inv[i]=inv[p%i]*(p-p/i)%p;
}
void NTT(ll c[],int n,int tp=1){
for(int i=0;i<n;i++){
r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
if(i<r[i])swap(c[i],c[r[i]]);
}
for(int i=1;i<n;i<<=1){
for(int j=0;j<n;j+=(i<<1)){
for(int k=0;k<i;k++){
ll x=c[j+k],y=gn[tp!=1][nn/i*k]*c[j+k+i]%p;
c[j+k]=add(x,y);
c[j+k+i]=cut(x,y);
}
}
}
}
void INTT(ll c[],int n){
NTT(c,n,-1);
for(int i=0;i<n;i++)c[i]=c[i]*inv[n]%p;
}7.任意模数FFT
给定\(n,m,P\),再给定次数界为\(n\)的第一个多项式和次数界为\(m\)的第二个多项式,求两个多项式的卷积模\(P\)。
注意:拆系数FFT精度损失极大,需要使用long double保证正确性。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
int x,n,m,l,r[262145],pm,p;
const long double pi=acos(-1);
struct complex{
long double re,im;
complex(long double re=0,long double im=0):re(re),im(im){}
complex operator+(const complex &b)const{return complex(re+b.re,im+b.im);}
complex operator-(const complex &b)const{return complex(re-b.re,im-b.im);}
complex operator*(const complex &b)const{return complex(re*b.re-im*b.im,re*b.im+im*b.re);}
}k1[262145],r1[262145],k2[262145],r2[262145],c1[262145],c2[262145],c3[262145];
void FFT(complex c[],int tp=1){
for(int i=0;i<n;i++)if(i<r[i])swap(c[i],c[r[i]]);
for(int i=1;i<n;i<<=1){
complex omn(cos(pi/i),tp*sin(pi/i));
for(int j=0;j<n;j+=(i<<1)){
complex om(1,0);
for(int k=0;k<i;k++,om=om*omn){
complex x=c[j+k],y=om*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}
void IFFT(complex c[]){
FFT(c,-1);
for(int i=0;i<=n;i++)c[i].re/=n;
}
void init(){
m+=n;
for(n=1;n<=m;n<<=1)l++;
for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
}
int main(){
scanf("%d%d%d",&n,&m,&p);
pm=sqrt(p);
for(int i=0;i<=n;i++){
scanf("%d",&x);
k1[i]=x/pm;
r1[i]=x%pm;
}
for(int i=0;i<=m;i++){
scanf("%d",&x);
k2[i]=x/pm;
r2[i]=x%pm;
}
init();
FFT(k1);
FFT(r1);
FFT(k2);
FFT(r2);
for(int i=0;i<=n;i++){
c1[i]=k1[i]*k2[i];
c2[i]=k1[i]*r2[i]+r1[i]*k2[i];
c3[i]=r1[i]*r2[i];
}
IFFT(c1);
IFFT(c2);
IFFT(c3);
for(int i=0;i<=m;i++){
ll s1=ll(c1[i].re+0.5)%p*pm%p*pm%p,s2=ll(c2[i].re+0.5)%p*pm%p,s3=ll(c3[i].re+0.5)%p;
printf("%lld ",((s1+s2)%p+s3)%p);
}
}7.多项式的运算
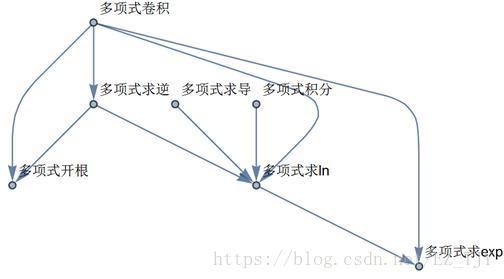
依赖关系:
直接按照公式打就好了。
我们先修改NTT:
void NTT(modp c[],int n,int tp=1){
for(int i=0;i<n;i++){
r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
if(i<r[i])swap(c[i],c[r[i]]);
}
for(int i=1,id=1;i<n;i<<=1,id++){
modp ggn=gn[id]^(tp==1?1:p-2);
for(int j=0;j<n;j+=(i<<1)){
modp gg=1;
for(int k=0;k<i;k++,gg=gg*ggn){
modp x=c[j+k],y=gg*c[j+k+i];
c[j+k]=x+y;
c[j+k+i]=x-y;
}
}
}
}
void INTT(modp c[],int n){
NTT(c,n,-1);
for(int i=0;i<n;i++)c[i]=c[i]/n;
}求逆:
void inverse(modp c[],int n=n){
static modp t[262145],tma[262145];
t[0]=c[0]^(p-2);
for(int k=2;k<=n;k<<=1){
for(int i=0;i<(k<<1);i++)tma[i]=(i<k?c[i]:0);
for(int i=(k>>1);i<(k<<1);i++)t[i]=0;
NTT(tma,k<<1);
NTT(t,k<<1);
for(int i=0;i<(k<<1);i++)t[i]=t[i]*2-t[i]*t[i]*tma[i];
INTT(t,k<<1);
}
memcpy(c,t,sizeof(int)*n);
}开根(\(c[0]=1\)):
void sqrt(modp c[],int n=n){
static modp t[262145],tma[262145],tmb[262145];
t[0]=1;
for(int k=2;k<=n;k<<=1){
for(int i=0;i<k;i++)tma[i]=t[i]*2;
inverse(tma,k);
for(int i=0;i<(k<<1);i++)tmb[i]=(i<k?c[i]:0);
NTT(tma,k<<1);
NTT(tmb,k<<1);
for(int i=0;i<(k<<1);i++){
modp tmp=tma[i];
tma[i]=t[i];
t[i]=tmp*tmb[i];
}
INTT(t,k<<1);
for(int i=0;i<(k<<1);i++)t[i]=(i<k?t[i]+tma[i]/2:0);
}
memcpy(c,t,sizeof(int)*n);
}求导:
void derivative(modp c[],int n=n){for(int i=0;i<n;i++)c[i]=c[i+1]*(i+1);}积分:
void integrate(modp c[],int n=n){for(int i=n-1;i>=1;i--)c[i]=c[i-1]*inv[i];c[0]=0;}求ln:
void ln(modp c[],int n=n){
static modp t[262145];
for(int i=0;i<(n<<1);i++)t[i]=(i<n?c[i]:0);
derivative(t,n);
inverse(c,n);
NTT(t,n<<1);
NTT(c,n<<1);
for(int i=0;i<(n<<1);i++)c[i]=c[i]*t[i];
INTT(c,n<<1);
for(int i=n;i<(n<<1);i++)c[i]=0;
integrate(c,n);
}求exp:
void exp(modp c[]){
static modp t[262145],ta[262145];
t[0]=1;
for(int k=2;k<=n;k<<=1){
for(int i=0;i<(k<<1);i++)ta[i]=t[i];
ln(ta,k);
for(int i=0;i<k;i++)ta[i]=c[i]-ta[i];
ta[0].a++;
NTT(t,k<<1);
NTT(ta,k<<1);
for(int i=0;i<(k<<1);i++)t[i]=t[i]*ta[i];
INTT(t,k<<1);
for(int i=k;i<(k<<1);i++)t[i]=0;
}
memcpy(c,t,sizeof(modp)*n);
}求幂:
我们在多项式求exp中假定了\(c[0]=1\),那么如果常数项不是\(1\)的话我们就把常数项变为\(1\)在运算后再用快速幂变回来即可。
void pow(modp c[],int k){
ln(c);
for(int i=0;i<n;i++)c[i]=c[i]*k;
exp(c);
}8、拉格朗日反演
1.形式幂级数
对于任意一个域\(F\)我们定义在其上的形式幂级数为:\[f(x)=\sum_{k=0}^\infty a_k x^k,a_k\in F\]
记所有的形式幂级数为\(F[[x]]\)。
2.反演公式
拉格朗日反演是求关于函数方程的幂级数展开系数非常重要的工具,可以用于组合计数函数的系数提取。
公式内容:
这里\([x^n]f(x)\)指取\(f(x)\)中\(x^n\)的系数。
若\(f(x),g(x)\in F[[x]]\)且\(f(g(x))=x\),则称\(f(x)\)为\(g(x)\)的复合逆。满足:\[[x^n]g(x)=\frac{1}{n}[x^{-1}]\frac{1}{f(x)^n}\tag{1}\]
特别的,如果\(f(x)=\displaystyle\frac{x}{\phi(x)}\),那么有:\[[x^n]g(x)=\frac{1}{n}[x^{n-1}]\phi(x)^n\tag{2}\]
公式的推导:
由式\(f(x)=\displaystyle\frac{x}{\phi(x)}\),得\(\phi(x)=\displaystyle\frac{x}{f(x)}\),代入\((2)\)式可得:\[[x^n]g(x)=\frac{1}{n}[x^{n-1}]\left(\frac{x}{f(x)}\right)^n\]
公式的推广:
\[[x^n]h(g(x))=\frac{1}{n}[x^{n-1}]h'(x)\left(\frac{x}{f(x)}\right)^n\]