线搜索方法
线搜索方法的基本过程都是在每一次迭代中先计算出一个优化方向\(p_k\),再在这个方向上对目标函数做一维优化,即选取合适的\(\alpha_k\),使\(x_{k+1}=x_k+\alpha p_k\)达到优化目的。一般来说,选取\(p_k=-B_k^{--1}\nabla f_k\),其中\(B_k\)是一个对称正定矩阵,\(B_k\)的选取有多种选择,比如在牛顿法中,\(B_k\)就是Hessian,而在逆牛顿法中,\(B_k\)是Hessian的近似。由于\(p_k=-B_k^{--1}\nabla f_k\),\(B_k\)正定,可以知道\(p_k\)确实是下降方向。
搜索步长
定义\[\Phi(\alpha)=f(x_k+\alpha p_k) \quad \alpha >0\]步长选取就是该函数的局部最优化问题,对此不需要太高的准确度,不能在这个问题上花费很多时间,所以只需要给出一个差不多的解就可以了。步长搜索过程分为两个阶段--bracketing-phase和bisection(or interpolation)-phase,前者找到一个包含期望步长的区间,后者在这个区间里面计算出一个好的步长。为此,先给搜索步长施加几个要求,首先就是搜索步长需要使得函数下降,但这显然不够,于是还有下面的条件。
Wolfe Condition
充分下降条件
\[f(x_k+\alpha p_k) \leq f(x_k)+c_1\alpha \nabla f_k^T p_k\]
示意图:
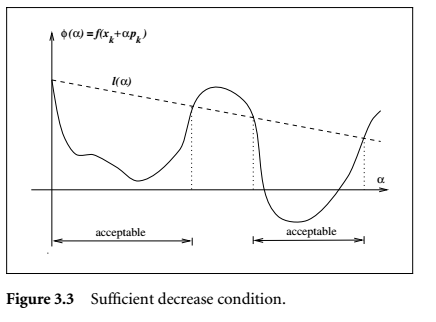
curvature condition
\[\nabla f (x_k+\alpha_k p_k)^Tp_k \geq c_2\nabla f_k^T p_k \quad 0 < c_1<c_2<1\]
示意图:

两个条件合起来称为Wolfe-condition,在实际应用中,\(c_1\)通常取得比较小,比如\(10^{-4}\)。\(c_2\)在牛顿和拟牛顿方法中通常取0.9,在共轭梯度法中通常取0.1。
将curvature condition改为\[|\nabla f (x_k+\alpha_k p_k)^Tp_k| \leq c_2|\nabla f_k^T p_k|\]得到的条件称为strong Wolfe condition
在Wolfe condition和strong Wolfe condition下,满足条件的步长是存在的:

The Goldstein condition
Goldstein condition和Wolfe condition出发点相同,都是在保证充足的下降情况下,又避免搜索步长过小。\[f(x_k)+(1-c)\alpha_k \nabla f_k^T p_k \leq f(x_k+\alpha_k p_k)\leq f(x_k)+c\alpha_k \nabla f_k^T p_k\quad 0<c<\frac{1}{2}\]Goldstein condition相对于Wolfe condition的缺点是,它的第一个不等式有可能排除了所有极小点。
backtracking
即使只对步长施加充分下降条件,只要适当选取步长,也是可以的,这里就要用到称为backtracking的方法。

在这个过程中,初始步长在牛顿和拟牛顿方法中取为1,在其他方法中可取为不同的值。
## 收敛理论

其中\(\theta_k\)是\(\nabla f_k\)与\(p_k\)的夹角。将这个定理中的wolfe condition换为goldstein 或strong wolfe定理任然成立。
最速下降法

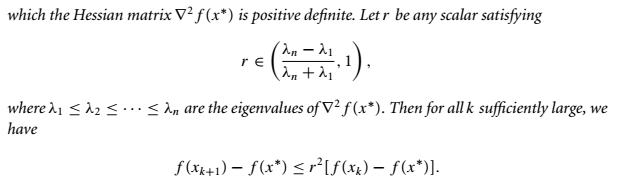
可知最速下降法收敛速度是线性的