Lecture 15: Matrix Factorization
Linear Network Hypothesis
Recommender System Revisited

在推荐系统问题中,我们有若干原始的训练数据,训练样本的输入\(\tilde x_n\)是用户ID,\(y_n=r_{nm}\),即ID为n的用户给电影m的评分
这里的输入特征是抽象、无实际意义的用户ID,我们希望从这些训练数据中学习出用户的特征(比如,用户对电影风格元素的喜好)、电影的特征(比如,电影包含哪些风格元素)
首先,我们把这些训练数据转化一下,与用户n有关的数据合并成一个样本:
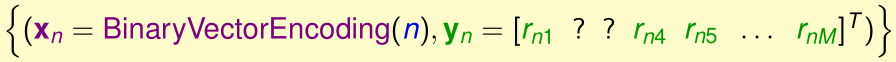
其中:
- \(x_n\)是经过BinaryVectorEncoding(One-hot encoding)过的N维向量,该向量中除第n个元素为1外,其他都为0
- \(y_n\)是一个M维向量,其中第m个元素表示用户n给电影m的评分\(r_{nm}\)
我们用转化后的训练集来训练一个线性神经网络:
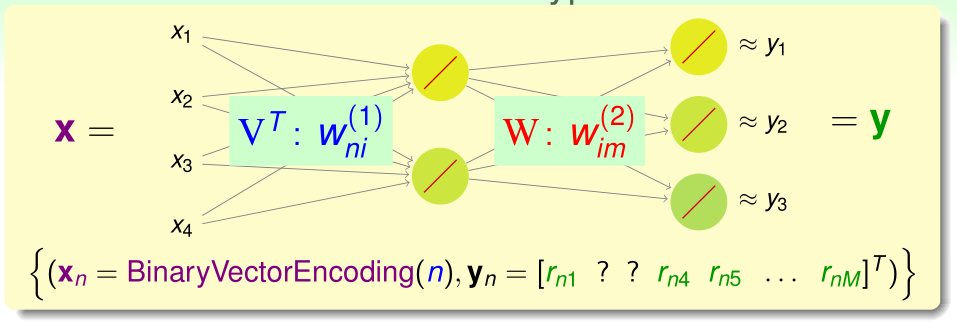
(该网络没有偏置,而且由于输入中只有一个\(x_n=1\),其他的都为0,所以隐含层激励函数不必选择tanh等函数,而是线性函数)
我们令\((V^T)_{ni}=w_{ni}^{(1)}\),\((W)_{im}=w_{im}^{(2)}\),则这个神经网络的输出向量可以表示为:
\[h(x)=W^TVx\]
对于用户n而言,设\(v_n=\)V的第n个列向量,则\(Vx_n=v_n\),\(h(x_n)=W^Tv_n\)
Basic Matrix Factorization
Linear Network: Linear Model Per Movie
设\(w_m^T\)是\(W^T\)的第m行,我们用这个神经网络预测用户n对电影m的评分为:
\[h_m(x_n)=w_m^Tv_n\]
由于对于每个用户n,有一些电影是没有评过分的,所以这个神经网络的损失函数比较特别:

也就是只有那些被用户n评过分的电影才会被计入损失函数
Matrix Factorization
如果我们已知矩阵\(W,V\),则
\[r_{nm}\approx h_m(x_n)=w_m^Tv_n=v_n^Tw_m\]
(\(v_n^T\)是\(V^T\)的第n行,\(w_m\)是\(W\)的第m列)
据此我们可以构造矩阵\(R\in\mathbb R^{N\times M}\),\(R=V^TW\),\((R)_{nm}=r_{nm}\):

在矩阵分解中,我们相当于把已知的矩阵\(R\)分解成两个矩阵\(V^T,W\)的乘积,\(v_n\)可以表示用户n的特征,而\(w_m\)可以表示电影m的特征
Matrix Factorization Learning
现在我们的任务是通过已知的\(r_{nm}\)学习出矩阵V和W
回顾一下该问题的损失函数:

其中,和式前的系数对最优化\(E_{in}\)没有影响,可以省去:
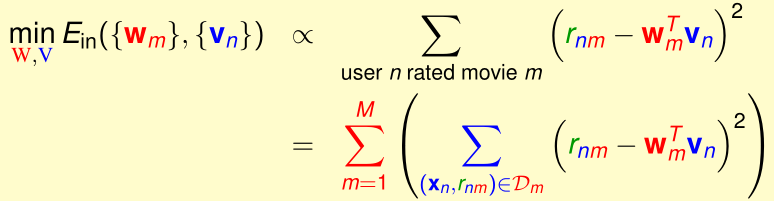
这个优化问题中有两组变量W和V,如果我们固定其中一个不变,优化另外一个的话,就可以视为线性回归问题:
比如现在固定W,优化V,那么我们分别对\(v_1,\cdots,v_N\)做优化,在优化\(v_n\)时,我们可以将这个问题视为有若干个训练样本\((w_m,r_{nm})\)的线性回归问题
于是我们可以使用最小二乘法,交替地对W和V作优化:

一般我们是随机初始化\(W,V\),\(E_{in}\)随着迭代进行会不断收敛。我们称这种算法叫交替最小二乘法(alternating least squares)
Stochastic Gradient Descent
Another Possibility: Stochastic Gradient Descent
对于上述问题,我们还可以用随机梯度下降的方法最优化
假设现在输入训练样本\(r_{nm}\),那么在单个样本上的误差为:


当\(i\neq n,j\neq m\)时有:
\[\nabla_{v_i}err=0\]
\[\nabla_{w_j}err=0\]
据此我们可以得到最优化矩阵分解的参数V和W的随机梯度下降法:

在大规模矩阵分解问题中,随机梯度下降法是最常用的方法