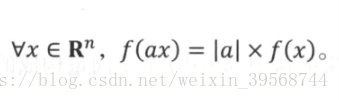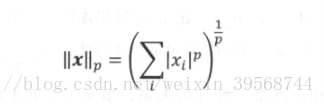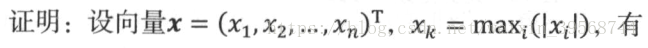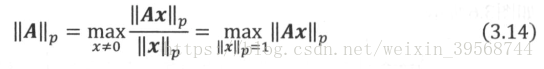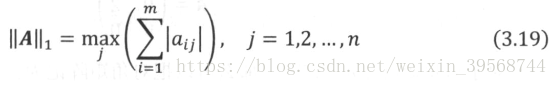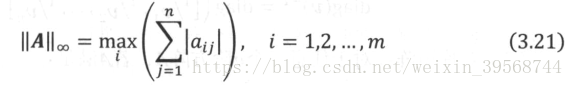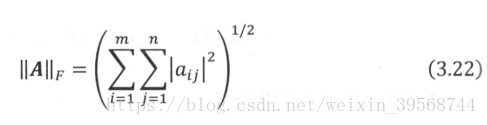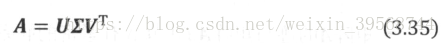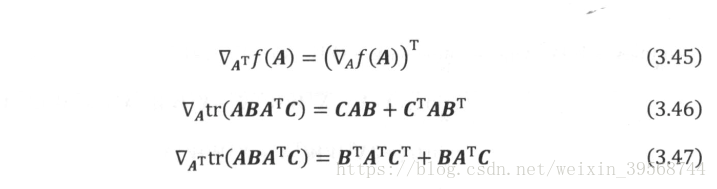本文主要总结一些在深度学习领域中比较重要的线性代数基础,过于基础的内容没有进行总结。
一.张量(tensor):在深度学习领域,很多时候数据都是高于二维的,因此,需要一种能够表示任意维度的数据类型,这就是张量。
二.范数(Norm):范数是数学中的一种基本概念,在泛函分析中,范数是一种定义在赋范线性空间中的函数,满足相应条件后的函数都可以被称为范数。下面主要介绍向量范数和矩阵范数并给出常用的几种范数计算公式。
1.向量范数
在泛函分析中,向量范数是衡量向量大小的一种度量方式。在形式上,向量范数是一个定义域为任意线性空间向量的函数,他把一个向量v映射为一个非负实数值R,即满足f:v->R
从几何角度来说,向量x的范数是度量从原点O到点x的距离。从广义角度来说,对于任意一个函数f:v->R,f只要同时满足下面3个条件个条件就可以成为范数。
(1)非负性:f(x)>=0,且当f(x)=0时,必有x=0成立。
(2)三角不等式性:f(x+y)<=f(x)+f(y)
(3)齐次性:
在机器学习中,特别是在模型最优化时,范数是正则化的主要手段,用于衡量模型的复杂度,其中最常用到的是p范数,p属于R,p>=1。p范数的定义为:
0范数:这是一个特殊的p-范数,他表示向量中非0元素的个数。注意,0-范数不是通过上式来定义。事实上我们会发现0范数不是真正的范数,因为他并不满足前面提到的齐次性性质,也就是f(ax)不等于|a|×f(x),这是因为一个向量乘上一个实数a,若a不等于0,那么该操作并不会 改变向量中非0元素的个数。
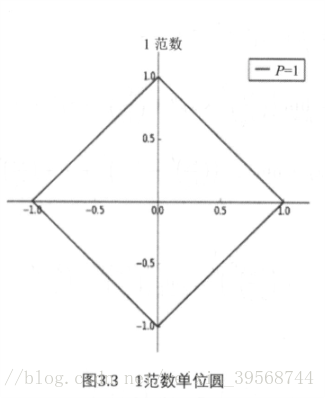
1范数:也被称为绝对值范数,大小等于向量的每个元素绝对值之和,即:
其中1范数中的单位范数即满足||x||=1的点{(x1,x2)},如图3.3所示:
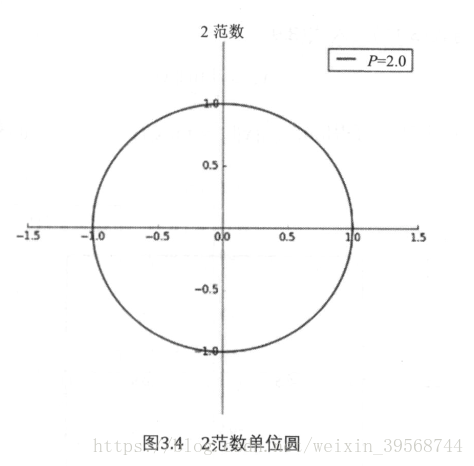
2范数:也被称为欧几里得范数,他的大小表示从原点到当前点的欧几里得距离,即:
2范数也是通常意义上的模,如下图:

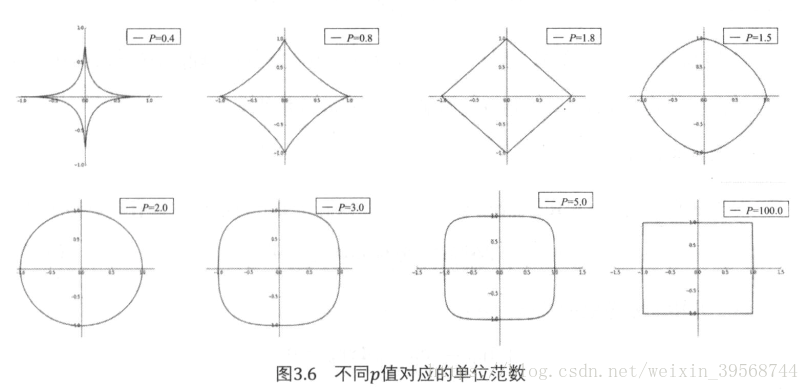
对于一个二维向量x=(x1,x2)^T,他的单位范数随p值增加的变化过程如下:
2.矩阵范数
上面讨论了常用的向量范数,范数的概念同样可以推广到矩阵领域,由此产生了矩阵范数的概念:对于任意一个函数f:A->R,函数f只要同时满足下面4个条件就可以称为矩阵范数:
(1)非负性:f(A)>=0,且当f(A)=0时,必要A=0成立
(2)齐次性:任取A属于R(m×n),f(aA)=|a|×f(A)
(3)三角不等式性:f(A+B)<=f(A)+f(B)
(4)矩阵乘法的相容性:对于任意两个可乘的矩阵A属于R(m×k)和矩阵B属于R(k×n),满足f(AB)<=f(A)×f(B)
为了与向量范数对应,用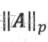
定义1:设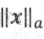

成立则称矩阵范数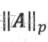
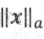
定义2:设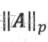
则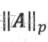
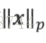
由向量p范数,可以诱导出常用的矩阵p范数。
1范数:记为
矩阵1范数也称为列和范数。
2范数:记为
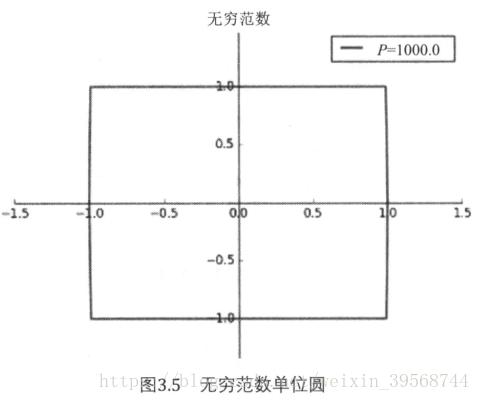
无穷范数:记为
矩阵无穷范数也被称为行和范数。
此外,在深度学习中,还经常用到另外一个矩阵范数,称为Frobenious范数,简称F范数,其定义为:
特殊的矩阵与向量:(1)对角矩阵(2)对称矩阵(3)单位向量(4)正交向量(5)正交矩阵
特征值分解:分而治之是算法设计的一种常用策略,通过把一个物体分解为不同的子部分,有时可以更好地理解整体特性。
奇异值分解:
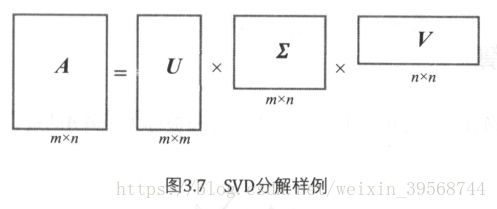
奇异值分解(Singular Value Decompositon,简称SVD),是线性代数中另一种非常重要的矩阵分解算法,特征值分解只适用于n阶方阵,并且不是所有的n阶方阵都存在特征分解,而SVD的应用更广,它适用于任意给定的m×n阶实数矩阵A。除了适用于将维,SVD还能应用于很多机器学习的工程领域,下图展示了SVD的分解样例:
形式化来说,设矩阵
在很多情况下,不需要使分解的结果准确还原矩阵A,只需要接近于A即可。事实上,奇异值与特征值的性质相似,在中间的对角矩阵中也是从大到小排列,而且奇异值的值减少特别快,在很多情况下,前百分之10甚至百分之1的奇异值的和就已经占了全部的奇异值之和的百分之99以上了。也就是说,可以用前r大的奇异值来近似描述矩阵,因此可以将式子化简为约等于。
迹运算: