【图的连通性】建造道路Road Construction

【图的连通性】建造道路Road Construction

题目描述

给定一个双向连通的公路网，当某些公路路段检修的时候可能会由于该段公路不通，可能会使某些旅游点之间无法通行，求至少新建多少条公路，使得任意对一段公路进行检修的时候，所有的旅游景点之间仍然畅通。

一共有N个旅游点，M段公路。

输入

第1行：2个整数，N,M（3<=N<=1000, 2<=M<=1000）

接下来M行，每行2个整数，表示一段公路连接的2个旅游点的编号

输出

第1行：1个整数，表示要修建的公路的数量

样例输入

10 12
1 2
1 3
1 4
2 5
2 6
5 6
3 7
3 8
7 8
4 9
4 10
9 10

样例输出

2

首先建立模型：

给定一个连通的无向图G，至少要添加几条边，才能使其变为边-双连通图（因为在修道路是一条边！）。

模型很简单，正在施工的道路我们可以认为那条边被删除了。那么一个图G能够在删除任意一条边后，仍然是连通的，当且仅当图G至少为边双连通的。
PS：不要问我为什么不是3-连通、4-连通…人家题目问“至少添加几条边”好不…

显然，当图G存在桥（割边）的时候，它必定不是边双连通的。桥的两个端点必定分别属于图G的两个【边双连通分量】（注意不是点双连通分量），一旦删除了桥，这两个【边双连通分量】必定断开，图G就不连通了。但是如果在两个【边双连通分量】之间再添加一条边，桥就不再是桥了，这两个【边双连通分量】之间也就是边双连通了。

那么如果图G有多个【边双连通分量】呢？至少应该添加多少条边，才能使得任意两个【边双连通分量】之间都是边双连通的（也就是图G是边双连通的）？

这个问题就是本题的问题。要解决这个问题：

1、 首先要找出图G的所有【边双连通分量】。

Tarjan算法用来寻找图G的所有【边双连通分量】是最简单有效的方法，因为Tarjan算法在DFS过程中会对图G所有的结点都生成一个Low值，而由于题目已表明任意两个结点之间不会出现重边，因此Low值相同的两个结点必定在同一个【边双连通分量】中（但是！！low值不同的点并不代表就不在同一个边双连通分量中，因为由于先后访问的顺序的原因，low值可能会不同，这跟并查集的道理是一样的，如果不进行压缩路径，几乎很多人的直接上级都不会是该团队的boss，这点可以模仿并查集的方式将其归到只有两层，查起来就很快了，否则可能超时！！当然你不考虑这点也能AC，水果了那些简单数据，但是下面这2组数据你可能过不了）！

11 14
1 2
1 3
1 4
2 5
6 11
2 6
5 6
5 11
3 7
3 8
7 8
4 9
4 10
9 10

11 14
1 2
1 3
1 4
5 11
2 5
2 6
5 6
6 11
3 7
3 8
7 8
4 9
4 10
9 10

以上两个测试数据的ans都是2。

2、 把每一个【边双连通分量】都看做一个点（即【缩点】）

也有人称【缩点】为【块】，都是一样的。其实缩点不是真的缩点，只要利用Low值对图G的点分类处理，就已经缩点了。

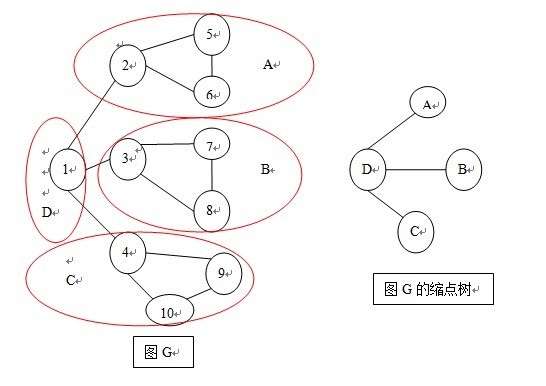
以样例1为例，样例1得到的图G为上左图，

其中Low[4]=Low[9]=Low[10]

   Low[3]=Low[7]=Low[8]

   Low[2]=Low[5]=Low[6]

   Low[1]独自为政....

把Low值相同的点划分为一类，每一类就是一个【边双连通分量】，也就是【缩点】了，不难发现，连接【缩点】之间的边，都是图G的桥，那么我们就得到了上右图以缩点为结点，以桥为树边所构造成的树。

　　以上这样以low值判断边连通分量是没有错的！只是要确保low值能区分出该块，当然，你可以用栈，就像求点双连通分量那样（并不是完全一样，那是以割点来区分的，这是以桥来区分的）。

3、 问题再次被转化为“至少在缩点树上增加多少条树边，使得这棵树变为一个边双连通图”。

首先知道一条等式：

若要使得任意一棵树，在增加若干条边后，变成一个双连通图，那么

至少增加的边数 =（ 这棵树总度数为1的结点数 + 1 ）/ 2

（证明就不证明了，自己画几棵树比划一下就知道了）

那么我们只需求缩点树中总度数为1的结点数（不一定是叶子数，如果树根仅有1个孩子，同样要将其统计进来）有多少就可以了。换而言之，我们只需求出所有缩点的度数，然后判断度数为1的缩点有几个，问题就解决了。

4、 求出所有缩点的度数的方法

两两枚举图G的直接连通的点（如果求出了桥，那么枚举桥也行的，相同于直接枚举树的边），只要这两个点不在同一个【缩点】中，那么它们各自所在的【缩点】的度数都+1。注意由于图G时无向图，这样做会使得所有【缩点】的度数都是真实度数的2倍，必须除2后再判断是否度为1。

特别注意：求【点双连通分量】与【边双连通分量】是不同的模板，勿混淆。

【AC代码】

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <stdlib.h>
#include <math.h>
#include <ctype.h>
#include <queue>
#include <map>
#include <set>
#include <algorithm>

using namespace std;
int head[1200], cnt, index1, ans;
int vis[1200], dfn[1200], low[1200], du[1200];
struct node
{
    int u, v, next;
}edge[100000];
void add(int u, int v)
{
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
void tarjan(int u, int fa)
{
    low[u]=dfn[u]=++index1;
    vis[u]=1;
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].v;
        if(v==fa) continue ;
        if(!vis[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
        }
        else if(v!=fa)
            low[u]=min(low[u],dfn[v]);
    }
}
void init()
{
    memset(head,-1,sizeof(head));
    cnt=0;
    memset(vis,0,sizeof(vis));
    memset(dfn,0,sizeof(dfn));
    index1=ans=0;
    memset(du,0,sizeof(du));
}
int main()
{
    int n, m, u, v, i, j;
    scanf("%d%d",&n,&m); 

        init();
        while(m--)
        {
            scanf("%d%d",&u,&v);
            add(u,v);
            add(v,u);
        }
        tarjan(1,-1);
        for(i=1;i<=n;i++)
        {
            for(j=head[i];j!=-1;j=edge[j].next)
            {
                int v=edge[j].v;
                if(low[v]!=low[i])
                {
                    du[low[i]]++;
                }
            }
        }
        for(i=1;i<=n;i++)
        {
            if(du[i]==1)
                ans++;
        }
        printf("%d\n",(ans+1)/2);

    return 0;
}