写这篇东西的原因
我就是不会FFT怎么了!我只会念法法塔
复数?
大佬嫌我不懂复数,觉得我太LJ了,于是便Diss我。
复数:形如
的数。
n次单位复数根:
n次单位复数根恰好有n个,即:
其中,i为虚数单位。
代表单位圆上的一点,原点与其所在射线
的正半轴成角
。
所以n次单位复数根可看作是一个指针转一圈,又回到(1,0)。
几个最重要的原理:
1.消去引理
2.折半引理
如果n为偶数且n>0,则n次单位复数跟的平方 的集合就是n/2次单位复数根的集合。
用消去引理证明。
3.求和引理
,有
等比数列求和。
分母显然不为0,因为
.
一些基本概念
1.次数界:多项式的最高项的次数+1.
2.系数表示:
3*.点值和插值:
点值表示:由点值对组成的集合。
一般地,一个次数界为n的多项式的点值表示,
其中,每个x必须互不相同。
点值运算:根据多项式A(x)的系数表示,得到多项式的点值表示的过程。
插值运算:点值运算的逆运算。假设现有一个n个点值对的点值表达,那么我们可以确定唯一的一个次数界为n的多项式。
为什么?考虑高斯消元。不就是解一个一次方程组吗?
最简单的例子:两点确定一条直线,三点确定一条抛物线。
!!!4.FFT原理
考虑以下两个东西。
1.点值表示的多项式乘法。2.对乘法结果进行插值运算。
1.点值表示的多项式乘法
对于两个多项式A,B,它们是被两个相同个点值对表示的唯一多项式
确定一组x,则有
令
,则可得到C的点值表示
显然,要用2n对来表示A,B,不然计算不了C。
显然时间复杂度:
2.对乘法结果进行插值运算
确定多项式C的系数。
进入正题
DFT
DFT:离散傅里叶变换(Discrete Fourier Transform)
进行点值操作!
有大佬将整个傅里叶变换从头到尾看一遍,由于我是菜鸡,看不懂。
目标:计算一个次数界为n的多项式
在n次单位复数根处的值(共n个)
说白了就是用n个n次单位复数根代入进去A(x),求出每一个
令
y即为a的DFT。记为
//这个a是A的系数,记得这一点。
IDFT
IDFT:即逆DFT。
进行插值操作!
现已知有n个点值对的点值表示
,可以确定一个次数界为n的唯一的多项式
结论:
证明:
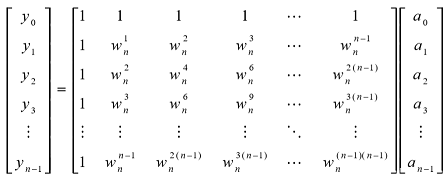
实际上就是
所以将插值运算改成y与
的乘积。
其中,
,其中
求证:
处的元素为
证明?矩阵乘法学过没?
这个证明方法的主要思路:需要证明当
时,
,当
时,
将式子划开,让i和j在同一个式子里扯上关系。
当
时,显然,
否则,由求和引理,
应用到多项式乘法?
FFT做两个多项式A,B的乘法的过程,实际上就是将A,B分别DFT一下,即进行点值操作。
此时得到了点值对为2n的点值表示,
扫一遍,
。
接着对C进行IDFT,完成插值操作。
FFT主要部分
1.FFT是基于分治策略的。二分。
为了方便计算,n必须满足一个大前提:n为2的正整数幂。
这种策略的优点:利用了复数单位根复数根的特殊性质。
次数界缩小了一半!
2.问题转化
原问题:求多项式
在n个n次单位复数根
的函数值。
现问题:求多项式
在n个n次单位复数根的平方的函数值。
上面加粗的字是FFT的一个主要的内容。
首先出场的是折半引理。根据它,n个n次单位复数根的平方实际上是由n/2个n/2次单位复数根组成,每个根恰好出现2次。(无聊说一句,就像一个指针转了2圈)
3.得出DFT的大致步骤
(I)对于目前的
得出
的系数。
(II)求出
的点值表示。
(III)
时间复杂度:
即
4.IDFT操作
根据
,直接套DFT,改某些地方即可。
(I)用
替换
,再把计算结果的每个元素除以n。
时间复杂度:
即
FFT的实现
上面讲了实现方法。现在侧重于实现过程。
1.点值表示的多项式乘法。
2.对乘法结果进行插值运算。
伪代码1
void FFT(a){
n=多项式a的次数界;
if(n=1)return a;
w_n=(cos(2pi*i/n),sin(2pi*i/n));
w_kn=1;
得到a0,a1的系数。
得到a0的DFT y0,a1的DFT y1
for k=0 to n/2-1{
y[k]=y0[k]+w_nk*y1[k];
y[k+n/2]=y0[k]-w_nk*y1[k];
}
return y;
}解释一下最后的循环部分。
实际上就是求出a的DFT y。
通过{}里的2行神操作,可以得出来a的DFT y。
看不懂第二个式子的,尝试理解下面这一段话。
减号,代表着正好转了半圈。
还记得上文的一句话么?(无聊说一句,就像一个指针转了2圈)
想象一下这个过程,在第k时刻和第k+(n/2)时刻,指针停留的位置是一样的!!!
所以
这招挺妙的。
程序优化
上述做法不是很好。需要优化。
PS:感谢前来观看博客的大佬们,但是到这里为止,还是不能够写出代码的。请继续读完下一部分,谢谢。
因为,根据位移和起始点的规律,可以对已有数组直接计算,不需要递归。
考虑当前问题处理的是哪些系数:
尝试发现下表的规律:

将i转化为的二进制,然后反过来设这个数为rev(i),则在开始的时候,i和rev(i)换个位置即可。
即第rev(i)个位置放
如何
求rev(i)?
考虑这个式子:
这是什么意思?
假设求出了rev(i/2),那么在i/2后面添加一个数,就相当于rev(i/2)向后挪1位。显然rev(i/2)是偶数。因为i/2的二进制第一位是0。
至于rev(i)的第一位是什么?取决于i的最后一位。
目标:不用递归,顺着做。
方法:模拟递归的回溯过程,顺序保存求出的值。注意,转移的时候,间隔是一样的。
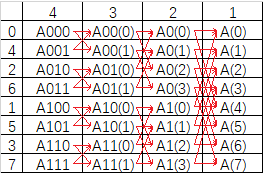
在回溯的过程中,两个次数界为k的多项式合并为一个次数界为2k的多项式。
最后合并出来的那个那n个值就是
。
IDFT也按照上述过程就好了,不要忘记所有的元素需要除以n。
程序实现
void FFT(Cpx *y,int opz){
int i,h,k;
fo(i,0,m-1)if(i<Rev[i])swap(y[i],y[Rev[i]]);
for(h=2;h<=m;h<<=1){
Cpx wn(cos(2*Pi/h),opz*sin(2*Pi/h));
for(i=0;i<m;i+=h){
Cpx w(1,0);
fo(k,i,i+(h>>1)-1){
Cpx u=y[k],t=w*y[k+(h>>1)];
y[k]=u+t;
y[k+(h>>1)]=u-t;
w=w*wn;
}
}
}
if(opz==-1){
fo(i,0,m-1)y[i].r/=m;
}
}
void Mul(LL *a,LL *b,LL *c){
int i;
fo(i,0,mo-1)f1[i]=Cpx(b[i],0);
fo(i,mo,m-1)f1[i]=Cpx(0,0);
fo(i,0,mo-1)f2[i]=Cpx(c[i],0);
fo(i,mo,m-1)f2[i]=Cpx(0,0);
FFT(f1,1);
FFT(f2,1);
fo(i,0,m-1)f1[i]=f1[i]*f2[i];
FFT(f1,-1);
fo(i,0,mo-1)a[i]=(LL)(f1[i].r+0.5)%mo;
}参考资料
yl《快速傅里叶变换》
lyc《从多项式乘法到傅里叶变换》
