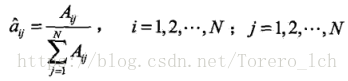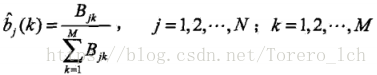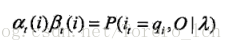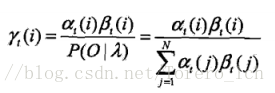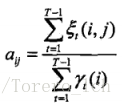2.3 HMM模型的学习
上一篇博客HMM隐马尔科夫模型。
2.3.1 监督学习方法
已知观测序列和对应状态序列时,可以直接使用极大似然估计MLE估计HMM的参数A,B,Π。
初始概率:S个样本中初始状态为i的频率。
转移概率:
观测概率:
2.3.2 Baum-Welch算法
Baum-Welch在很多地方又称前向-后向算法,一种用来学习HMM模型参数的方法。
首先来看我们的问题,要在观测序列已知,对应的状态序列未知的情况下估计出HMM的参数,典型的含有隐变量的概率模型参数估计问题,于是可以用EM算法的思想来解决。由于EM算法中的Q函数不太直观,实际意义也不好理解(对Q函数真的很无力(●ˇ∀ˇ●) ),本文换一个更直观的说法来描述这个算法。
直观地理解EM算法,它也可被看作为一个逐次逼近算法:事先并不知道模型的参数,可以随机的选择一套参数或者事先粗略地给定某个初始参数λ0 ,确定出对应于这组参数的最可能的训练样本状态(隐变量的情况),然后在当前的状态下再由此时的样本对参数修正,重新估计参数λ ,并在新的参数下重新确定模型的状态,这样,通过多次的迭代,循环直至某个收敛条件满足为止,就可以使得模型的参数逐渐逼近真实参数。 -- 参考自我爱自然语言处理
按照上面的说法,当随机初始化模型后,有了HMM模型λ、和观测序列O,联想之前的两个应用,此时我们可以求λ产生O的概率,和推测出最有可能的隐藏状态序列,但现在我们要估计的是不同状态间的转移概率和发射概率以及初始概率。
先来看转移概率,状态i转移到j的概率= i转移到j的概率 / i出现的概率;跟2.3.1中类似。
划重点,这里可以通过前向概率和后向概率的实际意义来理解,也可以推导出来:
最后得到:
划重点,条件概率转换成了前向概率和后向概率的乘积!,怎么得来的呢,本来想用条件概率公式推导一下,结果卒╥﹏╥... ,只能从实际意义来理解它了,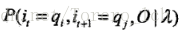
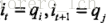
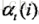
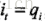

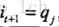
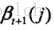
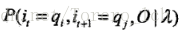
最后得到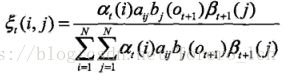

得到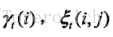
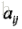
同理,发射概率=状态i出现且该时刻的观察到的是k/ i出现的概率;
初始概率就更直接了,根据
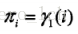
此时,就完成一次递推了,然后按照这样的计算方式不断循环,直至达到某个收敛条件即可。
上面是直观的理解,既然是EM算法,也应该有严格的推导。