转自:
https://blog.csdn.net/c20180630/article/details/70175814
二分图的概念
二分图又称作二部图,是图论中的一种特殊模型。
设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y,并且图中每条边连接的两个顶点一个在X中,另一个在Y中,则称图G为二分图。
二分图的性质
定理:当且仅当无向图G的每一个回路的次数均是偶数时,G才是一个二分图。如果无回路,相当于任一回路的次数为0,故也视为二分图。
二分图的判定
如果一个图是连通的,可以用如下的方法判定是否是二分图:
在图中任选一顶点v,定义其距离标号为0,然后把它的邻接点的距离标号均设为1,接着把所有标号为1的邻接点均标号为2(如果该点未标号的话),如图所示,以此类推。
标号过程可以用一次BFS实现。标号后,所有标号为奇数的点归为X部,标号为偶数的点归为Y部。
接下来,二分图的判定就是依次检查每条边,看两个端点是否是一个在X部,一个在Y部。
如果一个图不连通,则在每个连通块中作判定。
二分图匹配
给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
图中加粗的边是数量为2的匹配。
最大匹配
选择边数最大的子图称为图的最大匹配问题(maximal matching problem)
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
图中所示为一个最大匹配,但不是完全匹配。
增广路径
增广路径的定义:设M为二分图G已匹配边的集合,若P是图G中一条连通两个未匹配顶点的路径(P的起点在X部,终点在Y部,反之亦可),并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
增广路径是一条“交错轨”。也就是说, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且起点和终点还没有被选择过,这样交错进行,显然P有奇数条边(为什么?)
寻找增广路
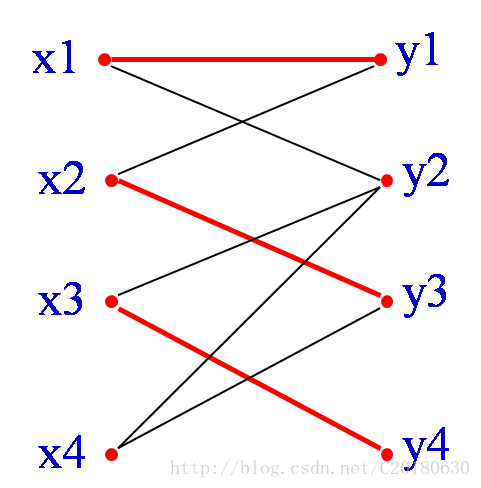
红边为三条已经匹配的边。从X部一个未匹配的顶点x4开始,找一条路径:
x4,y3,x2,y1,x1,y2x4,y3,x2,y1,x1,y2
因为y2是Y部中未匹配的顶点,故所找路径是增广路径。
其中有属于匹配M的边为{x2,y3},{x1,y1}
不属于匹配的边为{x4,y3},{x2, y1}, {x1,y2}
可以看出:不属于匹配的边要多一条!
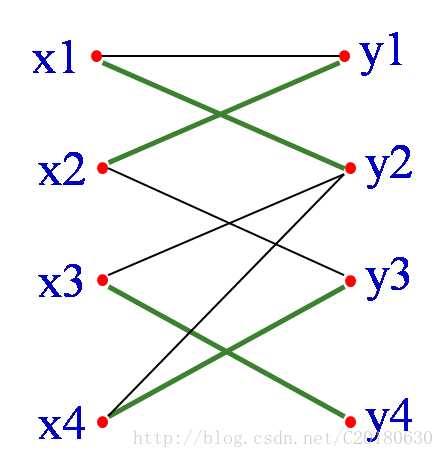
如果从M中抽走{x2,y3},{x1,y1},并加入{x4,y3},{x2, y1}, {x1,y2},也就是将增广路所有的边进行”反色”,则可以得到四条边的匹配M’={{x3,y4}, {x4,y3},{x2, y1}, {x1,y2}}
容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对。另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路.
可知四条边的匹配是最大匹配
增广路径性质
由增广路的定义可以推出下述三个结论:
- P的路径长度必定为奇数,第一条边和最后一条边都不属于M,因为两个端点分属两个集合,且未匹配。
- P经过取反操作可以得到一个更大的匹配M’。
- M为G的最大匹配当且仅当不存在相对于M的增广路径。
匈牙利算法
用增广路求最大匹配(称作匈牙利算法,匈牙利数学家Edmonds于1965年提出)
算法轮廓:
- 置M为空
- 找出一条增广路径P,通过取反操作获得更大的匹配M’代替M
- 重复2操作直到找不出增广路径为止
找增广路径的算法
我们采用DFS的办法找一条增广路径:
从X部一个未匹配的顶点u开始,找一个未访问的邻接点v(v一定是Y部顶点)。对于v,分两种情况:
- 如果v未匹配,则已经找到一条增广路
- 如果v已经匹配,则取出v的匹配顶点w(w一定是X部顶点),边(w,v)目前是匹配的,根据“取反”的想法,要将(w,v)改为未匹配,(u,v)设为匹配,能实现这一点的条件是看从w为起点能否新找到一条增广路径P’。如果行,则u-v-P’就是一条以u为起点的增广路径。
匈牙利算法
cx[i]表示与X部i点匹配的Y部顶点编号
cy[i]表示与Y部i点匹配的X部顶点编号
//伪代码
bool dfs(int u)//寻找从u出发的增广路径
{
for each v∈u的邻接点
if(v未访问){
标记v已访问;
if(v未匹配||dfs(cy[v])){
cx[u]=v;
cy[v]=u;
return true;//有从u出发的增广路径
}
}
return false;//无法找到从u出发的增广路径
}
//代码
bool dfs(int u){
for(int v=1;v<=m;v++)
if(t[u][v]&&!vis[v]){
vis[v]=1;
if(cy[v]==-1||dfs(cy[v])){
cx[u]=v;cy[v]=u;
return 1;
}
}
return 0;
}
void maxmatch()//匈牙利算法主函数
{
int ans=0;
memset(cx,0xff,sizeof cx);
memset(cy,0xff,sizeof cy);
for(int i=0;i<=nx;i++)
if(cx[i]==-1)//如果i未匹配
{
memset(visit,false,sizeof(visit)) ;
ans += dfs(i);
}
return ans ;
} 算法分析
算法的核心是找增广路径的过程DFS
对于每个可以与u匹配的顶点v,假如它未被匹配,可以直接用v与u匹配;
如果v已与顶点w匹配,那么只需调用dfs(w)来求证w是否可以与其它顶点匹配,如果dfs(w)返回true的话,仍可以使v与u匹配;如果dfs(w)返回false,则检查u的下一个邻接点…….
在dfs时,要标记访问过的顶点(visit[j]=true),以防死循环和重复计算;每次在主过程中开始一次dfs前,所有的顶点都是未标记的。
主过程只需对每个X部的顶点调用dfs,如果返回一次true,就对最大匹配数加一;一个简单的循环就求出了最大匹配的数目。
时空分析
- 时间复杂度:
- 找一次增广路径的时间为:
- 邻接矩阵: O(n^2)
- 邻接表:O(n+m)
- 总时间:
- 邻接矩阵:O(n^3)
- 邻接表:O(nm)
- 找一次增广路径的时间为:
- 空间复杂度:
- 邻接矩阵:O(n^2)
- 邻接表: O(m+n)
KM算法
最佳匹配
什么是完美匹配
如果一个二分图,X部和Y部的顶点数相等,若存在一个匹配包含X部与Y部的所有顶点,则称为完美匹配。
换句话说:若二分图X部的每一个顶点都与Y中的一个顶点匹配,**并且**Y部中的每一个顶点也与X部中的一个顶点匹配,则该匹配为完美匹配。
什么是完备匹配
如果一个二分图,X部中的每一个顶点都与Y部中的一个顶点匹配,**或者**Y部中的每一个顶点也与X部中的一个顶点匹配,则该匹配为完备匹配。
什么是最佳匹配
带权二分图的权值最大的完备匹配称为最佳匹配。
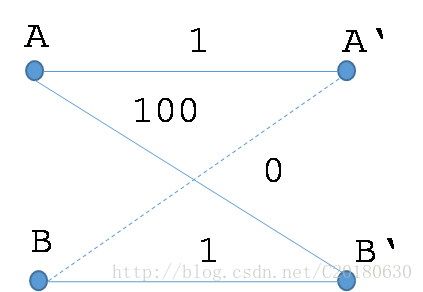
二分图的最佳匹配不一定是二分图的最大权匹配。
转化
可以添加一些权值为0的边,使得最佳匹配和最大权匹配统一起来。
KM算法
求二分图的最佳匹配有一个非常优秀的算法,可以做到O(N^3),这就是KM算法。该算法描述如下:
1.首先选择顶点数较少的为X部,初始时对X部的每一个顶点设置顶标,顶标的值为该点关联的最大边的权值,Y部的顶点顶标为0。
2.对于X部中的每个顶点,在相等子图中利用匈牙利算法找一条增广路径,如果没有找到,则修改顶标,扩大相等子图,继续找增广路径。当每个点都找到增广路径时,此时意味着每个点都在匹配中,即找到了二分图的完备匹配。该完备匹配即为二分图的最佳匹配。
什么是相等子图呢?因为每个顶点有一个顶标,如果我们选择边权等于两端点的顶标之和的边,它们组成的图称为相等子图。
如果从X部中的某个点Xi出发在相等子图中没有找到增广路径,我们是如何修改顶标的呢?如果我们没有找到增广路径,则我们一定找到了许多条从Xi出发并结束于X部的匹配边与未匹配边交替出现的路径,姑且称之为交错树。我们将交错树中X部的顶点顶标减去一个值d,交错树中属于Y部的顶点顶标加上一个值d。这个值后面要讲它如何计算。那么我们会发现:
-
两端都在交错树中的边(i,j),其顶标和没有变化。也就是说,它原来属于相等子图,现在仍属于相等子图。
-
两端都不在交错树中的边(i,j),其顶标也没有变化。也就是说,它原来属于(或不属于)相等子图,现在仍属于(或不属于)相等子图。
-
X端不在交错树中,Y端在交错树中的边(i,j),它的顶标和会增大。它原来不属于相等子图,现在仍不属于相等子图。
-
X端在交错树中,Y端不在交错树中的边(i,j),它的顶标和会减小。也就说,它原来不属于相等子图,现在可能进入了相等子图,因而使相等子图得到了扩大。
-
我们修改顶标的目的就是要扩大相等子图。为了保证至少有一条边进入相等子图,我们可以在交错树的边中寻找顶标和与边权之差最小的边,这就是前面说的d值。将交错树中属于X部的顶点减去d,交错树中属于Y部的顶点加上d。则可以保证至少有一条边扩充进入相等子图。
3.当X部的所有顶点都找到了增广路径后,则找到了完备匹配,此完备匹配即为最佳匹配。
相等子图的若干性质
- 在任意时刻,相等子图上的最大权匹配一定小于等于相等子图的顶标和。
- 在任意时刻,相等子图的顶标和即为所有顶点的顶标和。
- 扩充相等子图后,相等子图的顶标和将会减小。
- 当相等子图的最大匹配为原图的完备匹配时,匹配边的权值和等于所有顶点的顶标和,此匹配即为最佳匹配。
代码
bool dfs(int s) //匈牙利算法找增广路径
{
visx[s]=1;
for(int i=1;i<=cnty;i++)
if(!visy[i]){
int t=wx[s]+wy[i]-dis[s][i];
if(t==0) {
visy[i]=1;
if(linky[i]==0||dfs(linky[i])){
linkx[s]=i,linky[i]=s;
return true;
}
}
else if(t>0) //找出边权与顶标和的最小的差值
{
if(t<minz)minz=t;
}
}
return false;
}
void km()
{
memset(linkx,0,sizeof linkx); //linkx[i]表示与X部中点i匹配的点
memset(linky,0,sizeof linky);
for(int i=1;i<=cntx;i++){
while(1){
minz=INF;
memset(visx,0,sizeof visx);
memset(visy,0,sizeof visy);
if(dfs(i))break;
for(int j=1;j<=cntx;j++) //将交错树中X部的点的顶标减去minz
if(visx[j])wx[j]-=minz;
for(int j=1;j<=cnty;j++) //将交错树中Y部的点的顶标加上minz
if(visy[j])wy[j]+=minz;
}
}
}